Complete Solutions to EXAMPLE of chapter SEQUENCES AND SERIES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | SEQUENCES AND SERIES |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Write the first three terms in the sequences defined by the following :
`a_n =2n + 5`.
View SolutionWrite the first three terms in the sequences defined by the following :
`a_n =(n-3)/4`.
View SolutionWrite the first five terms of the following functions whose nth terms are :
`a_n =2^n`.
View SolutionWrite the first five terms of the following functions whose nth terms are :
`t_n =(2n-3)/6`.
View SolutionWrite the first five terms of the following functions whose nth terms are :
`a(n)=(-1)^(n-1) 5^(n+1)`.
View SolutionWrite the first five terms of the following functions whose nth terms are :
`T_n= (n(n+1)(2n+1))/6`.
View SolutionWhat is the 20th term of the sequence defined by : `a_n = (n- 1) (2-n)(3+n)`?
View SolutionLet the sequence be defined as follows : `a_1=3`, `a_n =3a_(n-1)+2`, for all n> 1. Find the first four terms of the sequence.
View SolutionFind as indicated in the following case :
`t_(1)=1,t_(n)=2t_(n-1),(ngt 1) ,t_(6)` .
View SolutionFind as indicated in the following case :
`S_(n)=S_(n-1)-1,(ngt2), S_(1)=S_(2)=2,S_(5)`.
View SolutionFind the 960th and 961st terms of the sequence given by :

View SolutionLet a (n) be the finite sequence with 9 terms, a (1), a (2), ...... a(9) defined as follows :
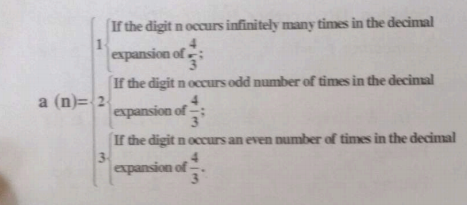 Find all the terms of the sequence.
Find all the terms of the sequence.
View SolutionFind 'd' and write the next four terms of the following arithmetic progression : `-1, 1/4, 3/2`,...........
View SolutionFind the nth term of the sequence 5,2,-1,-4,-7, ...........
View SolutionShow that the sequence : log a, log (ab), `log (ab^2)`, `log (ab^3)`,............... is an A.P. Find its nth term.
View SolutionWhich term in the A.P. 5, 2, -1, ... is -22 ?
View SolutionWhich term of the sequence : `20,19 1/4, 18 1/2, 17 3/4`, ..... is the first negative term ?
View SolutionWhich term of the sequence : 8-6i, 7 - 4i, 6- 2i,.......... is pure imaginary ?
View SolutionA sequence `{a_n}` is given by : `a_n=n^2-1, n in N`. Show that it is not an A.P.
View SolutionDetermine 2nd term and rth term of an A.P. whose 6th term is 12 and 8th term is 22 .
View SolutionDetermine the 25th term of an AP., whose 9th term is -6 and common difference is `5/4`.
View SolutionIf 7 times the 7th term of an A.P. is equal to 11 times its 11th term, show that the 18th term of the A.P. is zero.
View SolutionThe number of terms common to two AP's `3,7,11,"…,"407` and `2,9,16,"…,"709` is
View SolutionIf the pth, qth and rth terms of an A.P. be x,y,z repsectively, then show that : `x(q-r)+y(r-p)+z(p-q)=0`
View SolutionFind the sum of indicated number of terms of the following arithmetic progression : 16, 11, 6,..........., n terms, 23 terms.
View SolutionOut of l, a, n, d and `S_n`, determine the ones that are missing from the following : `a=17/2, d= 3/2, n=64`.
View SolutionFind the sum to n terms of the sequence `{a_n}`, where `a_n=5-6n, n in N`.
View SolutionIf the sum of n terms of an A.P is `nP+1/2 n(n-1)Q`, where P and Q are constant, find the common difference.
View SolutionDetermine the sum of first thirty five terms of an arithematic progression if `t_(2)=2` and `t_(7)=22`.
View SolutionFind the sum of all natural numbers lying between 100 and 1000, which are multiples of 5.
View SolutionIf the 12th term of an A.P. is -13 and the sum of the first four terms is 24, what is the sum of the first 10 terms ?
View SolutionFind the common difference of an A.P. whose first term is 100 and the sum of whose first six terms is five times the sum of the next six terms.
View SolutionFind the sum of all 3-digit numbers which leave remainder 2, when divided by 5.
View SolutionIf the sum of n terms of an A.P. is `3n^2 + 5n` and its `m^(th)` term is 164, find the value of m.
View SolutionThe sums of n terms of two arithmetic progressions are in the ratio `5n+ 4 : 9n + 6`. Find the ratio of their 18th terms.
View SolutionLet `S_(n)` denote the sum of n terms of an AP, if `S_(2n)=3S_(n)`, then the ratio `(S_(3n))/(S_(n))` is equal to
View SolutionFind the sum of first 24 terms of on AP `t_(1),t_(2),t_(3),"....",` if it is known that `t_(1) + t_(5) + t_(10) + t_(15) + t_(20) + t_(24)=225.`
View SolutionThe income of a person is ₹ 3,00,000 in the first year and receives an increase of % 10,000 to his income per year for the next 19 years. Find the total amount, he receives in 20 years.
View SolutionA manufacturer of PC’s produced 600 sets in the third year and 700 sets in the seventh year. Assuming that the production uniformly increases by a fixed number every year, find:- the production in the first year.
View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets I the seventh year. Assuming that the production increases uniformly by a fixed number every year, find : the production in the 10th year
View SolutionA manufacturer of TV sets produced 600 sets in the third year and 700 sets I the seventh year. Assuming that the production increases uniformly by a fixed number every year, find : the total production in first 7 years.
View SolutionInsert 3 A.M.’s between 3 and 19.
View SolutionThere are n arithmetic means between 3 and 17. The ratio of the last mean to the first mean is 3: 1. Find the value of n.
View SolutionThe sum of two numbers is `13/6`. An even number of arithmetic means are inserted between them and their sum exceeds their number by 1. Find the number of means inserted.
View SolutionIf `log_10 2, log_10(2^x- 1)` and `log_10(2^x+3)` are in A.P., then find the value of x.
View SolutionIf the roots of the equation : `a(b - c)x^2 +b (c - a)x + c(a - b) = 0 ` are equal, show that `1/a,1/b,1/c` are in A.P.
View SolutionThe sum of three numbers in A.P. is -3 and their product is 8. Find the numbers.
View SolutionFind four terms in A.P. whose sum is 20 and the sum of whose squares is 120.
View SolutionThe digits of a positive integer having three digits are in AP and their sum is 15. The number obtained by reversing the digits is 594 less then the original number. Find the number.
View SolutionIf the fourth Power of the common difference of an A.P. with integer entries is added to the product of any four consecutive terms of it, prove that the resulting Sum is the square of an integer.
View SolutionIf a, b, c are in A.P., prove that :
`(bc)^-1,(ca)^-1` and `(ab)^-1` are also in A.P.
View SolutionIf a, b, c are in A.P., prove that :
`(a(b+c))/(bc), (b(c+a))/ (ca), (c(a+b))/(ab)` are also in A.P.
View SolutionIf a, b, c are in A.P., prove that :
`(ab+ac)/(bc), (bc+ba)/ (ca), (ca+cb)/(ab)` are also in A.P.
View SolutionIf `a^(2),b^(2),c^(2)` are in A.P. Prove that `(a)/(b+c),(b)/(c+a),(c)/(a+b)` are also in A.P.
View SolutionIf `a^2 (b+c),b^2(c+a) , c^2(a+b)` are in A.P., show that : either a, b, c are in A.P. or ab + bc + ca =0.
View SolutionFind the indicated terms in the following : a= 1, r= 1.2 , `t_4, t_n`.
View SolutionFind the 10th term of the geometric series : 5+ 25 + 125 +........ Also, find its nth term.
View SolutionWhich term of the following sequence:- `2,2sqrt2,4`,.....is 128?
View SolutionThe first term of a G.P. is 1. The sum of the third term and fifth term is 90. Find the common ratio of G.P.
View SolutionFind a G.P. for which sum of the first two terms is -4 and the fifth term is 4 times the third term.
View SolutionIn a finite G.P., the product of the terms equidistant from the beginning and the end is always same and equal to the product of first and last terms.
View SolutionShow that the products of the corresponding terms of the sequences a, ar, `ar^2`,...`ar^(n-1)` and A, AR, `AR^2`,....`AR^(n-1)` form a G.P, and find the common ratio.
View SolutionIf the pth , qth , rth , terms of a GP . Are x,y,z respectively prove that : `x^(q-r).y^(r-p).z^(p-q)=1`
View SolutionProve that the product of first 'n' terms of a G.P., whose first term is ‘a’ and last term is` ‘l’ `, is `(al)^(n/2)`.
View SolutionThe number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour ?
View SolutionEvaluate : `sum_(j=1)^10 {(1/2)^(j-1)+(1/5)^(j+1)}`.
View SolutionFind the sum of first n terms and the sum of first 5 terms of the geometric series : `1+2/3+4/9`+ .........
View SolutionDetermine the number n in a geometric progression `{a_n}`, if `a_1= 3, a_n= 96` and `S_n= 189`.
View SolutionFind the sum of the series : 11 + 103 + 1005 +.... to n terms.
View SolutionFind the sum to n terms of the series :
`(x+1/x)^2+(x^2 + 1/x^2)^2+ (x^3 + 1/x^3)^2+` ...... .
View SolutionFind the least value of n for which the sum 1 + 3 + `3^2` +...... to n terms is greater than 7000.
View SolutionSum to n terms : `4+ 44+ 444 +` ............
View SolutionFind the sum of the sequence 7, 77, 777, 7777,.....up to n terms.
View SolutionIf `S_n` denotes the sum of n terms of a G.P. whose first term and common ratio are a and r respectively, then :
`S_1 +S_3+S_5+.....+S_(2n-1)= (an)/(1-r)-(ar(1-r^(2n)))/((1-r)^2 (1+r))`.
View SolutionIf `f(x)` is a function satisfying `f(x+y)=f(x)f(y)` for all `xy in n` such that `f(1)=3` and `sum_(x=1)^(n)f(x)=120`. Then, the value of n is
View SolutionA person has 2 parents, 4 grand parents, 8 great-grand parents, and so on. Find the number of ancestors during the ten generations preceding his own.
View SolutionAn insect starts from a point and travels in a straight path 1 mm in the first second and half of the distance covered in the previous second in the succeeding second. In how much time would it reach a point 3 mm away from its starting point.
View SolutionInsert three numbers between the numbers 1 and 256 so that the resulting sequence is a G.P.
View SolutionA.M. between two numbers is 10 and their G.M is 8. Find the numbers.
View SolutionThe A.M. between two distinct positive numbers is twice the G.M. between them. Find the ratio of the greater to the smaller.
View SolutionIf one geometric mean G and two arithmetic means `A_1` and `A_2` be inserted between two given quantities, prove that : `G^2=(2A_1-A_2)(2A_2-A_1)`.
View SolutionFind the value of n so that `(a^(n+1)+ b^(n+1))/(a^n+b^n)` may be the geometric mean between a and b.
View SolutionFind all the sequences, which are simultaneously arithmetic and geometric progressions.
View SolutionThe sum of first three terms of a GP. is `13/12` and their product is - 1. Find the common ratio and the terms.
View SolutionThe product of first three terms of a G.P. is 1000. If we add 6 to its second term and 7 to its 3rd term, the three terms form an A.P. Find the terms of the G.P.
View SolutionThe sum of three numbers in G.P. is 56. If we subtract 1, 7, 21 from these numbers in that order, we obtain an arithmetic progression. Find the numbers.
View SolutionFind four numbers forming a geometric progression in which the third term is greater than the first term by 9, and the second term is greater than the 4th by 18.
View SolutionIf p, q, r are in A.P. while x, y, z are in G.P., prove that `x^(q-r).y^(r-p).z^(p-q) =1`.
View SolutionVerify that 10,-9, 8.1,..... is a geometric progression. Find the sum to infinity of the G.P.
View SolutionFind the sum to infinity of the G.P. `-3/4,3/16,-3/64`, .......
View SolutionProve that : `3^(1/2)xx3^(1/4)xx3^(1/8)xx.......... to oo=3`.
View SolutionThe first term of a G.P. is 2 and the sum to infinity is 6. Find the common ratio.
View SolutionIf `A=1+r^a+r^(2a)+ ......... to oo` and `B=1+r^b+r^(2b)+........... to oo` , prove that `r=((A-1)/A)^(1//a)=((B-1)/B)^(1//b)`.
View SolutionUse geometric series to express 0.555 = 0.5 as a rational number .
View SolutionEvaluate : `.23 bar 45`.
View SolutionWhich rational number has the decimal expansion `0.3 bar56` ?
View SolutionFor ``0ltphilt(pi)/(2)" if " x=sum_(n=0)^(oo)cos^(2n) phi,y=sum_(n=0)^(oo)sin^(2n)phi" and "z=sum_(n=0)^(oo)cos^(2n)phisin^(2n)phi`, then
View SolutionA square is drawn by joining the mid-points of the sides of a give square. A third square is drawn inside the scond square in the same way and this process continues indefiniely. If a side of the first square is 16 cm, then determine the sum of the areas of all the squares.
View SolutionFind the sum to infinity by finding the sum to n terms or directly of the series : `1+3/2+5/2^2+7/2^3`+ ...........
View SolutionIf the sum to infinity of the series : `3+(3 +d) xx 1/4 + (3 + 2d)xx1/4^2`+ .......... is `4 8/9`, find d. Also name the series.
View Solution
EXAMPLE questions and complete solutions for chapter SEQUENCES AND SERIES of MODERN PUBLICATION of Class 11