Complete Solutions to EXAMPLE of chapter STRAIGHT LINES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | STRAIGHT LINES |
| MODERN PUBLICATION | EXAMPLE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Plot the points (2,3), (-2,3), (-2,-3), (2,-3), (0,5), (-2,0) .
View SolutionIf three verticles of a rectangle are (0,0), (2, 0), and (0, 3), find the coordinates of the fourth vertex?
View SolutionThe base of an equilateral triangle with side 2a lies along the y-axis such that the mid-point of the base is at the origin. Find the vertices of triangle.
View SolutionFind the distance between the pair of points (5, -12) , (9,-9).
View SolutionFind a point on the x-axis which is equidistant from the points (7, 6) and (3, 4).
View SolutionDetermine, by distance formula whether the points (0, 0), (3, 2), (9, 6) lie on line ?
View SolutionShow that (8, 2), (5, - 3) and (0,0) are the vertices of an isosceles triangle.
View SolutionWithout using the pythagorus, show that the points (4, 4), (3, 5) and (-1, -1) are the vertices of a right angled triangle.
View SolutionFind the coordinates of a point which divides externally the line joining (1, -3) and (-3, 9) in the ratio 1 : 3.
View SolutionIn what ratio, the line joining (-1, 1) and (5, 7) is divided by the line `x+y=4`?
View SolutionThe vertices of a quadrilateral are at (- 2,4), (1, 3) (4,3) and (1,2). Show that the quadrilateral is a parallelogram.
View SolutionFind the point of intersection of the medians of the triangle with vertices at (- 1, 0), (5,- 2) and (8, 2).
View SolutionFind the area of the triangle whose vertices are (3, 8), (– 4, 2) and (5, 1).
View SolutionShow that the following triple of points are collinear : (2, 4), (0, 1), (4, 7).
View SolutionFind the values of x for which the points (x, -1), (2, 1) and (4, 5) are collinear.
View SolutionDraw a quadrilateral in the cartesian plane whose vertices are (-4,5), (0,7), (5,5) and (-4,- 2). Also find its area.
View SolutionProve that in a right angled triangle the mid-point of the hypotenuse is equidistant from its vertices.
View SolutionFind the equation of the set of all points equidistant from the point (4, 2) and the x-axis.
View SolutionFind the equation of the set of points such that the sum of its distances from (0, 2) and (0, - 2) is 6.
View SolutionA point moves such that the sum of its distance from two fixed points (ae, 0) and (-ae, 0) is always, 2a. Prove that the equation of the locus is `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`, where `b^(2)=a^(2)(1-e^(2))`
View SolutionThe Slope m of a line is given by : `m= sqrt3` . Find its inclination.
View SolutionThe slope of the line passing through the points (3,-2) and (-1,4) is:
View SolutionFind the slope of the line passing through the points :
(3, - 2) and (7, -2).
View SolutionDetermine `lambda` , so that 2 is the slope of the line through (2,5) and `(lambda,3)`
View SolutionA line passes through `(x_1, y_1)` and (h,k). If slope of the line is m, show that `k-y_1=m(h-x_1)`.
View SolutionState whether the two lines in the following problem is parallel, perpendicular or neither parallel nor perpendicular :
through (5,6) and (2,3), through (9,-2) and (6,-5).
View SolutionState whether the two lines in the following problem is parallel, perpendicular or neither parallel nor perpendicular :
Through (2, -5) and (-2, 5), through (6,3) and (1,1).
View SolutionLine through the points (-2,6) and (4 ,8) is perpendicular to the line through the points (8,12) and (x, 24). Find the value x.
View SolutionShow that the points (1, 1), (2, 3) and (3, 5) are collinear.
View SolutionA quadrilateral has the vertices at the points (-4, 2), (2, 6) (8, 5) and (9, - 7). Show that the mid-points of the sides of the quadrilateral are the vertices of a parallelogram.
View SolutionWithout using the distance formula, show that (- 2, - 1), (4, 0), (3, 3) and (- 3, 2) are the vertices of a parallelogram .
View SolutionIf A (2,0), B (0, 2) and C (0,7) are three vertices, taken in order, of an isosceles trapezium ABCD In which AB is parallel to DC. Obtain the co-ordinates of D.
View SolutionIn the figure, time- distance graph of a linear relation is given :
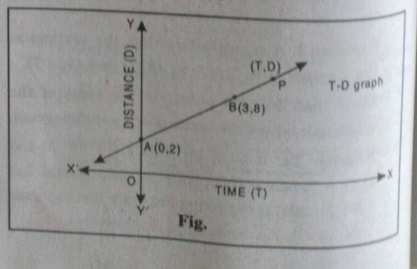 Two positions of time and distance recorded as:
When T = 0, D = 2 and when T = 3, D = 8.
Using the concept of slope, find the law of motion i.e. how distance depends upon time.
Two positions of time and distance recorded as:
When T = 0, D = 2 and when T = 3, D = 8.
Using the concept of slope, find the law of motion i.e. how distance depends upon time.
View SolutionFind the equation of the straight line, which is parallel to x-axis and 2 units above it.
View SolutionFind the equation of the straight line, which is parallel to y-axis and 3 units to the right of it.
View SolutionFind the equation of the line, which is parallel to y-axis and passing through the point (3, - 4).
View SolutionFind the equation of the st. line passing through the point (4, 3) with slope 2.
View SolutionFind the equation of the straight line bisecting the segment joining the points (5,3) and (4,4) and making an angle of `45^(@)` the positive direction of X- axis .
View SolutionFind the equation of the st. line passing through points (0,- 4) and (-6, 2).
View SolutionFind the equations of the sides of the triangle whose vertices are (- 1, 8), (4, - 2) and (- 5,- 3).
View SolutionThe perpendicular from the origin to a line meet at the point (-2, 9), find the equation of the line.
View SolutionA (-3,-1) and B (2, 2) are two adjacent vertices and O(3,0) is the point of intersection of the diagonals of a parallelogram ABCD. Write down the equations of the four sides of the parallelogram.
View SolutionShow that the points (1, 4), (3, - 2) and (- 3,16) are collinear and find the equation of the st. line an which they lie.
View SolutionFind the equation of the st. line with slope 3 and y-intercept - 2.
View SolutionFind the equation of a line through the origin, which makes an angle of `45^@` with the positive direction of x-axis.
View SolutionWrite the equation of the line for which `tan theta=1/2`, where `theta` is the inclination of the line and y-intercept is `-3/2`.
View SolutionWrite the equation of the line for which `tan theta=1/2`, where `theta` is the inclination of the line and x-intercept is 4.
View SolutionFind the equations of the lines passing through the point (2, 2) such that the sum of their intercepts on the axes is 9.
View SolutionFind the equations of the lines which cut off intercepts on the axes whose sum and product are 1 and -6 respectively.
View SolutionFind the equation of the line through (2,3) so that the segment of the line intercepted between the axes is bisected at this point
View SolutionFind the perpendicular form of the equation of the lines from the given values of p and `alpha` :
p=3 and `alpha = 45^@`.
View SolutionFind the perpendicular form of the equation of the lines from the given values of p and `alpha` :
p=5 and `alpha = 135^@`.
View SolutionIf p is the length of perpendicular from the origin to the line whose intercepts on the axes are a and b, then show that `(1)/(p^(2)) = (1)/(a^(2)) +(1)/(b^(2))`.
View SolutionFind the equation of a st. line, which passes through the point (-2,3) and makes an angle of `60^@` with the positive direction of x-axis.
View SolutionThe length L (in centimetres) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L = 125.134 when C = 110, express L in terms of C.
View SolutionFind the distance of the line 4x - y = 0 from the point P (4, 1) measured along the line making an angle of `135^@` with the positive x-axis.
View SolutionFind the equation of the st. line through (3, 4) and (2, -1).
View SolutionReduce the equation to `sqrt3x+y+1 =0` to the form y = mx +c and hence find the slope, the inclination to the x-axis and the intercept on the y-axis.
View SolutionFind the slope and y-intercept of the st. line 5x + 6y = 7.
View SolutionReduce the equation 2x-7y+3= 0 to the intercept form and hence find the intercepts on the axes.
View SolutionEquation of a line is 3x- 4y+10=0. Find its : slope .
View SolutionEquation of a line is 3x- 4y+10=0. Find its : x and y-intercepts.
View SolutionReduce the equation `sqrt3x+y-8=0` into normal form and find :
length of the perpendicular from origin to the line.
View SolutionReduce the equation `sqrt3x+y-8=0` into normal form and find :
angle between the normal and positive x-axis.
View SolutionFind the angle between the straight lines : `y- sqrt3 x-5=0` and `sqrt3 y-x+6=0`.
View SolutionTwo lines Passing through the point (2, 3) make an angle of `45^@`. If the slope of one of the lines is 2, find the slope of the other.
View SolutionDetermine the angle B of the triangle with vertices A (- 2, 1), B (2, 3) and C (- 2, - 4).
View SolutionFind tha angle between the lines joining the points (0,0) (2,3) and `(2,-2),(3,5)`
View SolutionThe line 7x-9y-19 = 0 is perpendicular to the line through the points (h, 3) and (4, 1). Find the value of h.
View SolutionFind the equation of the st. line through the origin making angle of `60^@` with the st. line `x +sqrt3y + 3sqrt3=0`.
View SolutionFind the equation of a line passing through the point (0,1) and parallel to : `3x-2y+5 = 0`.
View SolutionFind the equation of line perpendicular to x - 2y +3=0 and passing through the point (3,-2) .
View SolutionFind the equation of the right bisector of the line segment joining the points (3, 4) and (-1, 2).
View SolutionFind the image of the point (3, 8) with respect to the line `x+3y=7`, assuming line as a plane mirror.
View SolutionAssuming that straight line works as the plane mirror for a point, find the image of the point (1, 2) in the line x-3y+4=0.
View SolutionFor the triangle ABC whose vertices are A (-2, 3), B (4, - 3) and C (6, 5), find the equation of :
the perpendicular bisector of the side BC.
View SolutionFor the triangle ABC whose vertices are A (-2, 3), B (4, - 3) and C (6, 5), find the equation of :
the altitude from A.
View SolutionFor the triangle ABC whose vertices are A (-2, 3), B (4, - 3) and C (4, 5), find the equation of :
the st. line through A parallel to the opposite side BC.
View SolutionFind the point of intersection of the st. lines x - 4y = 3 and 6x - y= 11.
View SolutionIf 3x-by+2=0 and 9x+3y+a=0 represent the same straight line, find the values of a and b.
View SolutionThe sides of quadrilateral taken in order, are given by `3x + 11y -65 =0, 5x +y-39 = 0, -x + 5y + 13 = 0 and 11x-3y + 65 = 0`. Find the co-ordinates of the vertices of the quadrilateral.
View SolutionFind the point of intersection of the medians of the triangle with vertices at (- 1, 0), (5,- 2) and (8, 2).
View SolutionFind the coordinates of the foot of perpendicular from a point (-1, 3) to the line `3x-4y-16=0`.
View SolutionFind the centroid and incentre of the triangle whose vertices are (1, 2), (2, 3) and (3, 4).
View SolutionThe vertices of a triangle are (4, -3), (-2, 1) and (2, 3). Find the co-ordinates of the circumcentre of the triangle. [Circumcentre is the point of concurrence of the right-bisectors of the sides of a triangle.]
View SolutionShow that the area of the triangle formed by the lines whose equations are : `y=m_1x+c_1, y= m_2 x+c_2` and x=0 is : `((c_1-c_2)^2)/(2|m_1-m_2|)`.
View SolutionProve that the three st. lines : 2x - 3y = 7, 3x -4y = 13 and 8x-11y = 33 meet in a point.
View SolutionShow that the perpendicular bisectors of the sides of the triangle with vertices (7, 2), (5, -2) and (- 1, 0) are concurrent. Also find the co-ordinates of the point of concurrence (circumcentre).
View SolutionProve analytically that the altitudes of a triangle are concurrent.
View SolutionThe line-segment joining the mid-points of two sides of a triangle is parallel to the third side and ............. Of it.
View SolutionThe diagonals of a rectangle are of the equal length.
View SolutionThe diagonals of a rhombus are perpendicular to each other .
View SolutionProve that the figure formed by joining the points of the adjacent sides of a quadrilateral parallelogram.
View SolutionFind the distance between two Parallel lines :
`y=mx+c_1` and `y=mx+c_2`.
View SolutionFind the distance between two Parallel lines :
`ax + by +c_1 =0` and `ax + by +c_2 =0`.
View SolutionFind the distance between the st. line 4x + 3y- 5 = 0 and the point (- 2, - 1).
View SolutionFind the perpendicular distance of the point (b, a) from the st. line `x/a-y/b=1`.
View SolutionFind the point on the x-axis, whose distances from the line `(x)/(3)+(y)/(4)=1` are 4 units.
View SolutionShow that the origin is equidistant from the three straight lines : 4x + 3y + 10 = 0,5x - 12y + 26 =0 and 7x + 24y = 50.
View SolutionFind the distance between the parallel lines : `3x-4y+ 5 =0 and 3x - 4y + 7=0`.
View Solution
EXAMPLE questions and complete solutions for chapter STRAIGHT LINES of MODERN PUBLICATION of Class 11