Complete Solutions to NCERT QUESTIONS of chapter PROBABILITY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | PROBABILITY |
| NAGEEN PRAKASHAN | NCERT QUESTIONS |
| Number Of Questions | 43 |
| Academic Year | 2023-24 |
The coin is tossed three times.
View SolutionA dice is thrown two times.
View SolutionFind the number of possible outcomes of tossing a coin four times.
View SolutionA coin is tossed and a die is thrown
View SolutionA coin is tossed and then a die is rolled only in case a head is shown on the coin.
View Solution2 boys and 2 girls are in room P and 1 boy 3 girls are in room Q. write the sample space for the experiment in which a room is selected and then a person.
View SolutionDescribe the sample space for the indicated experiment : One die of red colour, one of white colour and one of blue colour are placed in a bag. One die is selected at random and rolled, its colour and the number on its uppermost face is noted
View SolutionAn experiment consists of recording boy-girl composition of families with 2 children. (i) What is the sample space if we are interested in knowing whether it is a boy or girl in the order of their births? (ii) What is the sample space if we are
View SolutionA box contains 1 red and 3 identical white balls. Two balls are drawn at random in succession without replacement. Write the sample space thise experiment.
View SolutionAn experiment consists of tossing a con and then throwing it second time if a head occurs. If a tail occurs on the first toss, then a die is rolled once. Find the sample space.
View SolutionSuppose 3 bulbs are selected at random form a lot. Each bulb is tested and classified as defective (D) or non-defective (N). Write the sample space of this experiment.
View SolutionA com is tossed. If the outcome is a head, a die is thrown. If the die shows up an even number, the die is thrown again. What is the sample space for the experiment?
View SolutionThe numbers 1,2,3 and 4 are written separately on four slips of paper. The slips are put in a box mixed thoroughly. A person draws two slips from the box, one after the other without replacement. Describe the sample space for the experiment.
View SolutionAn experiment consists of rolling a die and the tossing a coin once if the number on the die is even.If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.
View SolutionA coin is tossed. If it showsf a tail, we draw a ball from a box which contains 2 red and 3 black balls. If it shows head, we throw a die. Find the samle space for this experiment.
View SolutionA die is thrown repeatedly untill a six comes up. What is the sample space for this experiment?
View SolutionA die is rolled. Let E be the event die shows 4 and F be the event die shows even number. Are E and F mutually exclusive?
View SolutionA die is thrown. Describe the following events:
(i) A: number less than 7
(ii) B: a number greater than 7
(iii) C: a mutiple of 3
(iv) D: a number less than 4
(v) E: an even number greater than 4
(vi) F: a number not less than 3
Also find `AuuB, AnnB, BuuC, EnnF, DnnE, A-C, D-E, EnnF', F'`
View SolutionAn experiment involves rolling a pair of dice and recording the numbers that come up. Describe the following events: A: the sum is greater than 8, B: 2 occurs on either die C: the sum is at least 7 and a multiple of 3. Which pairs of these events
View SolutionThree coins are tossed once. Let A denote the event "three heads snow", B denote the event "two heads and one tail show", C denote the event three tails show and D denote the event "a head shows on the first coin". Which events are (i) mutually e
View SolutionThree coins are tossed. Describe (i) Two events which are mutually exclusive. (ii) Three events which are mutually exclusive and exhaustive. (iii) Two events, which are not mutually exclusive. (iv) Two events which are mutually exclusive but not exhaustiv
View SolutionTwo dice are thrown. The events A, B and C are as follows:
A: getting an even number on the first die.
B: getting an odd number on the first die.
C: getting the sum of the number on the first dice `le5`.
Describe the events
(i) `A'` (ii) not B (iii) A or B
(iv) A and B (v) A but not C (vi) B or C
(vii) B and C (viii) `AnnB'nnC'`
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space `S={W_(1),W_(2),W_(3),W_(4),W_(5),W_(6),W_(7)}`
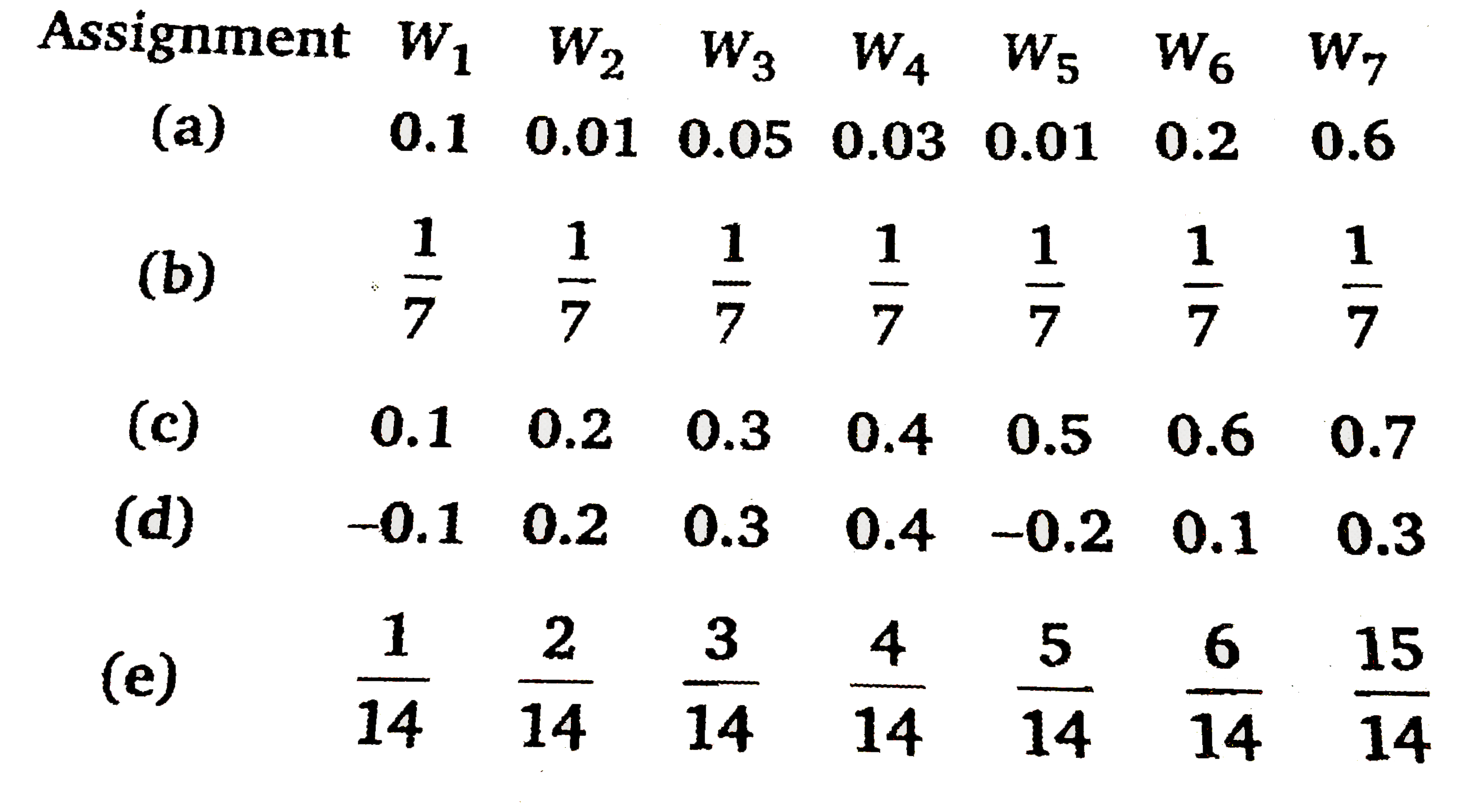
View SolutionA coin a tossed twice, that is the probability that at least one tail occurs?
View SolutionA die is thrown, find the probability of following events:
(i) A prime number will appear,
(ii) A number greater than or equal to 3 will appear,
(iii) A number less than or equal to one will appear,
(iv) A number more than 6 will appear,
(v) A number less than 6 will appear.
View SolutionA card is selected from a pack of 52 cards.
(a) How many points are there in the sample space?
(b) Calculate the probability that the card is an ace of spades.
(c) Calculate the probability that the card is (i) an ace (ii) black card.
View SolutionA fair coin with 1 marked on one face and 6 on the other and a fair die are both tossed. Find the probability that the sum of numbers that turn up is (i) 3 (ii) 12.
View SolutionThere are four men and six women on the city council. If one council member is selected for a committee at random how likely is it that it is a woman?
View SolutionA fair coin is tossed four times, and people win Re 1 for each head and lose Rs 1.50 for each tail that turns up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amount
View SolutionThree coins are tossed once. Fmd the probability of getting (i) 3 heads (ii) 2 heads (iii) atleast 2 heads (iv) atmost 2 heads (v) no head (vi) 3 tails (vii) exactly two tails (vm) no tail (ix) atmost two tails
View SolutionIf `2/(11)`is the probability of an event, what is the probability of the event not A
View SolutionA letter is chosen at random from the word ASSASSINATION. Find the probability that letter is (i) a vowel (ii) a consonant.
View SolutionIn a lottery, a person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by the lottery committee, he wins the prize. What is the probability of Winning the prize in the
View SolutionCheck whether the following probabilities `P(A)` and `P(B)` are consistently defined
(i) `P(A)=0.5,P(B)=0.7, P(AnnB)=0.6`
(ii) `P(A)=0.5, P(B)=0.4, P(AuuB)=0.8`
View SolutionFill in the blanks in following table:

View SolutionGiven `P(A)=3/5` and `P(B)=1/5` . Find `P(A "or" B)`, if A and B are mutually exclusive events.
View SolutionIf E and F are events such that `P(E)=1/4, P(F)=1/2` and `P(E"and"F)=1/8`, find (i) `P(E"or"F)` (ii) `P` (not E and not F).
View SolutionEvents E and F are such that `P` (not E or not F) `=0.25`. State whether E and F are mutually exclusive.
View SolutionA and B are events such that `P(A) = 0. 42`, `P(B) = 0. 48`and `P(A a n d B) = 0. 16`. Determine (i) P(not A), (ii) P(not B) and (iii) P(A or B)
View SolutionIn class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both mathematics and biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology or both.
View SolutionIn an entrance test that is graded on the basis of two examinations, the probability of a randomly chosen student passing the first examination is 0.8 and the probability of passing the second examination is 0.7. The probability of passing atleas
View SolutionThe probability that a student will pass the final examination in both English and Hindi is 0.5 and the probability of passing neither is 0.1. If the probability of passing the English examination is 0.75. What is the probability of passing the Hindi examination?
View SolutionIn a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find the probability that (i) The student opted for NCC or NSS. (ii) The student has opted neithe
View Solution
NCERT QUESTIONS questions and complete solutions for chapter PROBABILITY of NAGEEN MATHS (HINGLISH) of Class 11