Complete Solutions to Exercise of chapter THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | THERMODYNAMICS |
| NARENDRA AWASTHI | Exercise |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Out of molar entropy (I), specific volume (II), heat capacity (III), volume (IV), extensive properties are :
View SolutionOut of internal energy (I), boiling point (II), pH (III) and E.M.F. of the cell (IV) intensive properties are :
View SolutionThermodynamic equilibrium involves
View SolutionWhich has maximum internal energy at `290K` ?
View SolutionA `10g` piece of iron `( C =0.45 J//g^(@)C )` at `100^(@)C` is dropped into `25g` of water `( C =4.2 J//g^(@)C)` at `27^(@)C`. Find temperature of the rion and water system at thermal equilibrium .
View SolutionWhen freezing of a liquid takes place in a system it:
View SolutionMechanical work is specially important in systems that contain
View SolutionDetermine which of the following reactions taking place at constant pressure represents system that do work on the surrounding environment
`Ag^(+)(aq)+Cl^(-)(aq)rarrAgCl(s)" " (II) NH_(4)Cl(s)rarrNH_(3)(g)+HCl(g) " " (III) 2NH_(3)(g)rarrN_(2)(g)+3H_(2)(g)`
View SolutionDetermine which of the following reactions at constant pressure represent surrounding that do work on the system environment :
(P) `4NH_(3)(g) + 7O_(2)(g) to 4 NO_(2)+ 6H_(2)O(g)`
(Q) `CO.O(g)+ 2H_(2)(g) to CH_(3)OH(l)`
(R) `C("s,graphite")+H_(2)O(g) to CO(g)+H_(2)(g)`
(S) `H_(2)O(s) to H_(2)O(l)`
View SolutionA sample of liquid in a thermally insulated constant ( a calorimetre ) is strirred for 2 hr. by a mechancal linkage to motor in the surrounding ,for this procees :
View SolutionAn ideal gas expand against a constant external pressure at 2.0 atmosphere from 20 litre to 40 litre and absorb `10kJ` of energy from surrounding . What is the change in internal energy of the system ?
View Solution2 mole of zinc is dissolved in HCl at `25^(@)` C. The work done in open vessel is :
View SolutionA sample of an ideal gas is expanded `1 m^(3)` to `3 m^(3)` in a reversible process for which `P=KV^(2)` , with `K=6 "bar"//m^(6).` What is work done by the gas (in kJ) ?
View SolutionA given mass of gas expands from state `A` to state `B` by three paths `1,2`, and `3` as shown in the figure below. If `w_(1),w_(2)` and `w_(3)`, respectively, be the work done by the gas along three paths, then
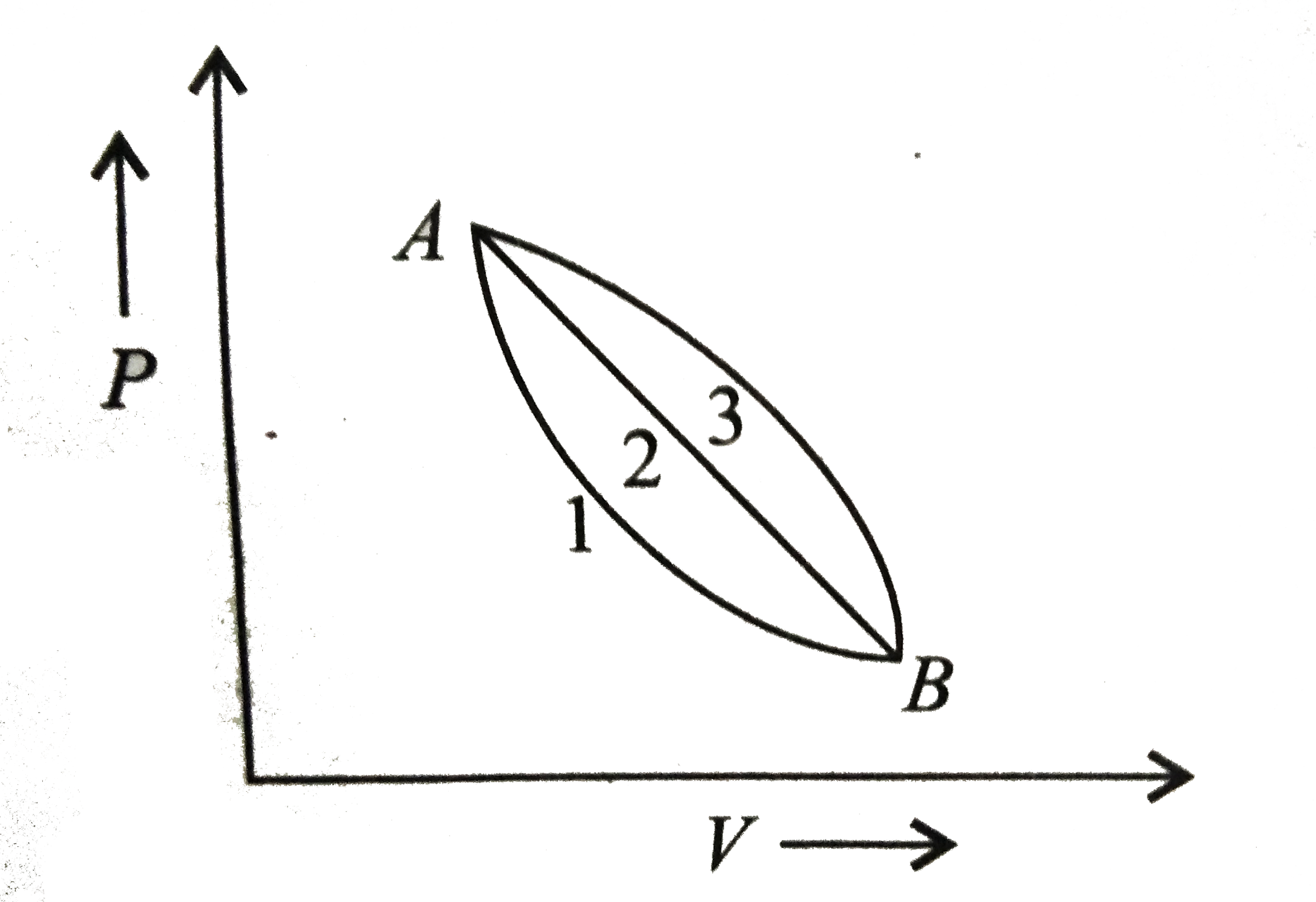
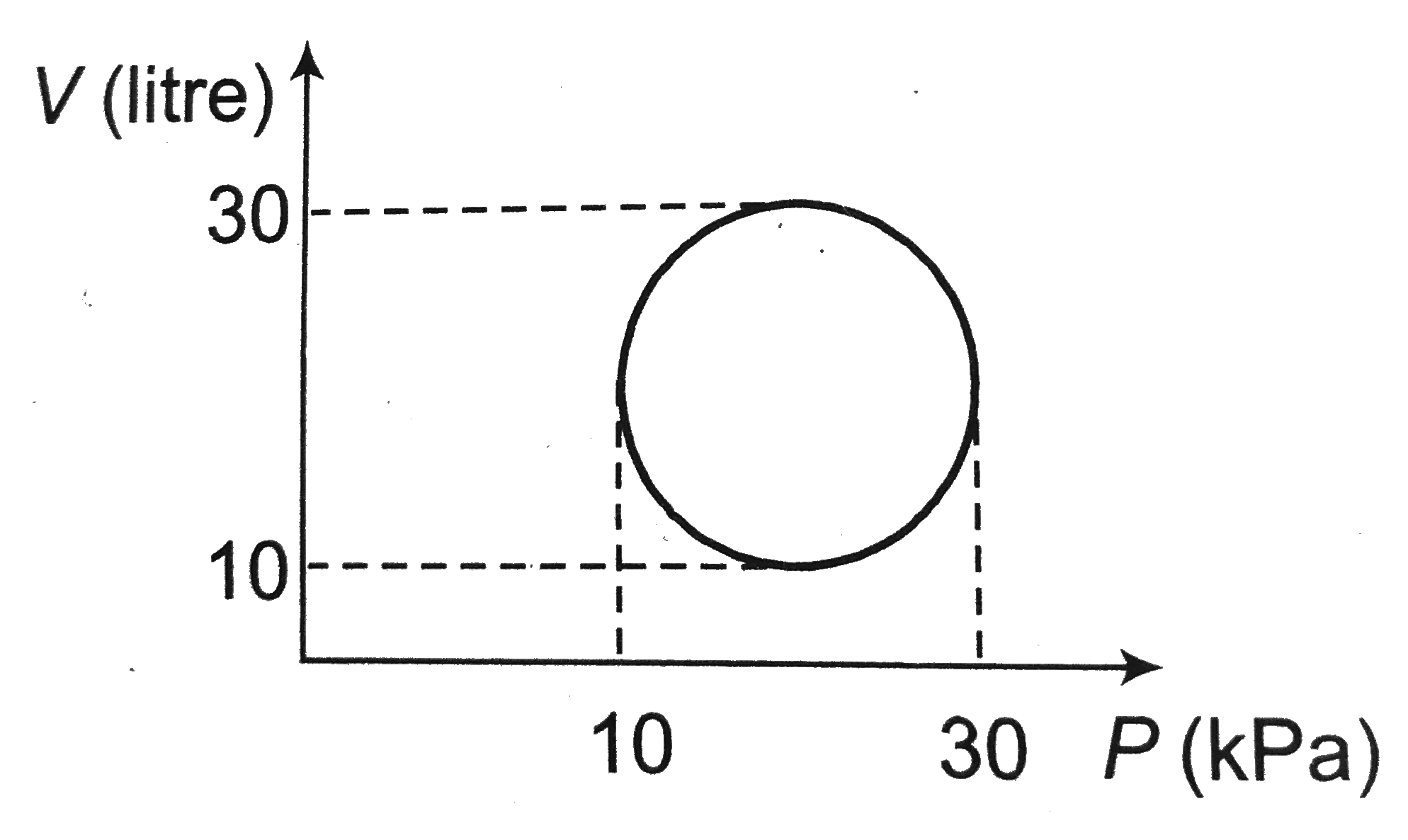
View SolutionHeat energy abosrbed by a system in going through a cyclic process shown in figure is
View Solution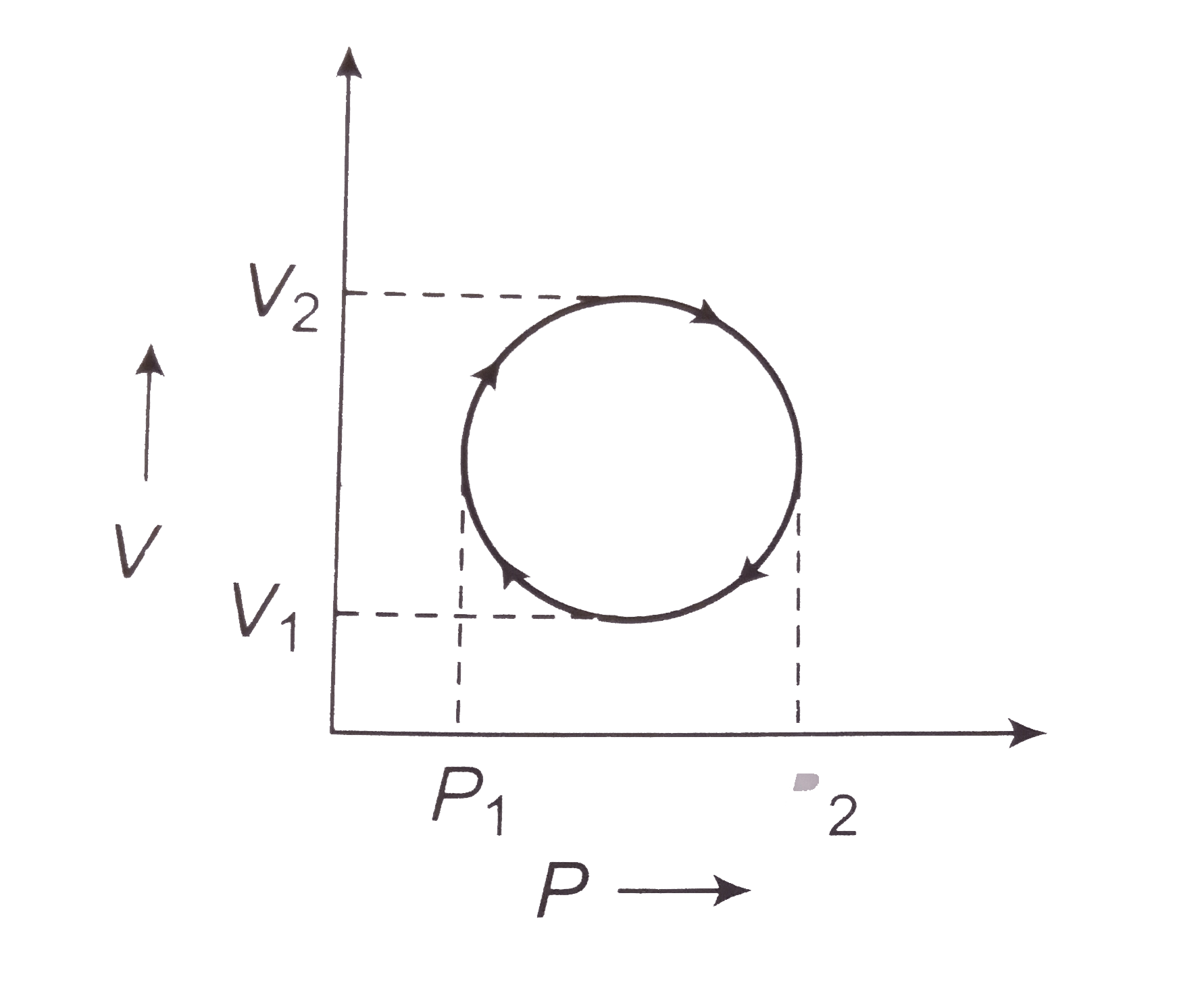
In the cyclic process shown in the `V-P` diagram the magnitude of the work is done is
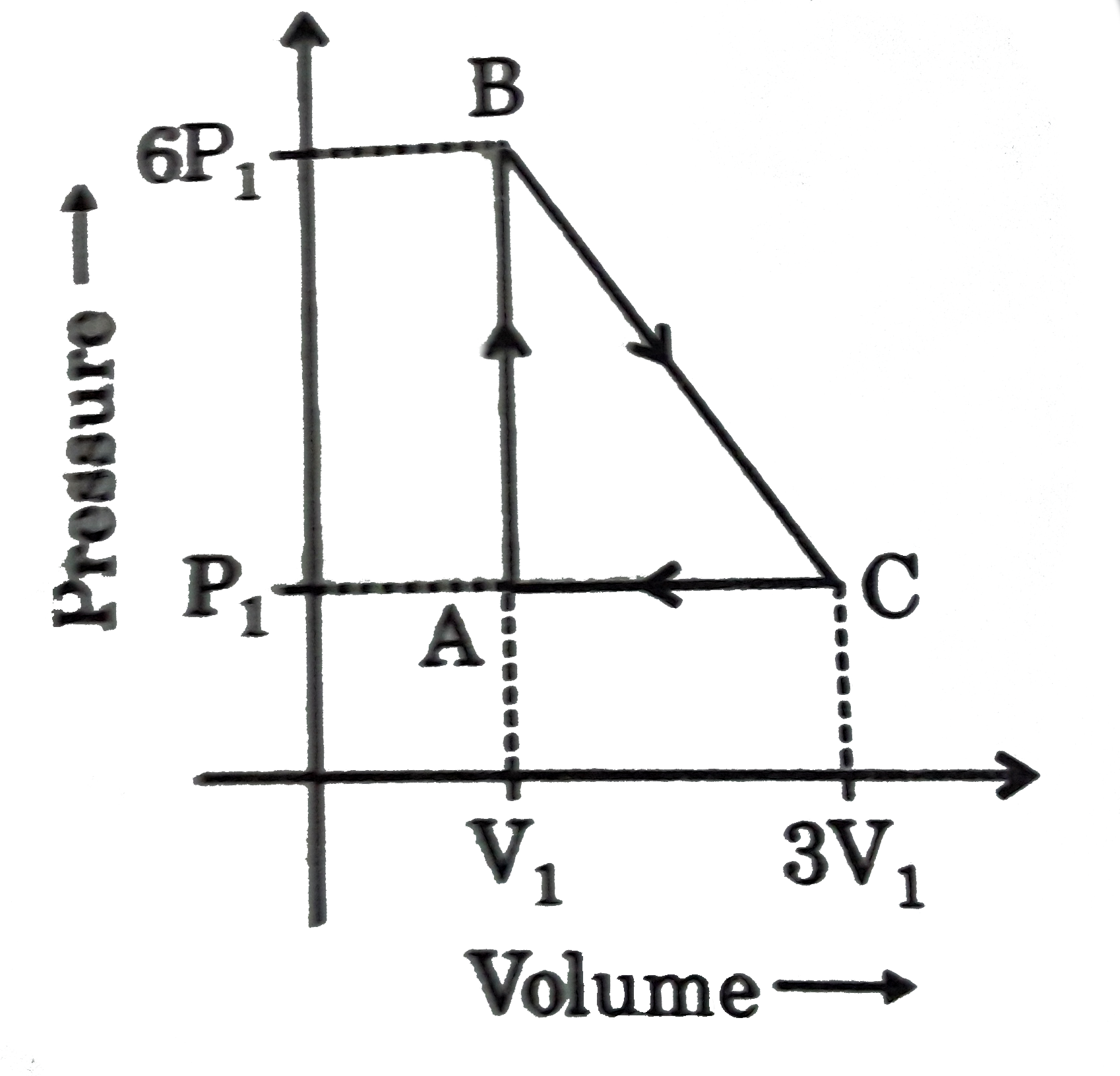
View SolutionAn ideal gas is taken around the cycle ABCA as shown in P-V diagram. The net work done by the gas during the cycle is equal to :
View SolutionAn ideal gas is at pressure P and temerature T in a box, which is kept in vaccum with in a large container. The wall of the box is punctured. What happens as the gas occupies entire container?
View SolutionIn following figs. Variation of volume by change of pressure is shown in Fig. A gas is taken along the path `ABCDA`. The change in internal energy of the tgas will be:
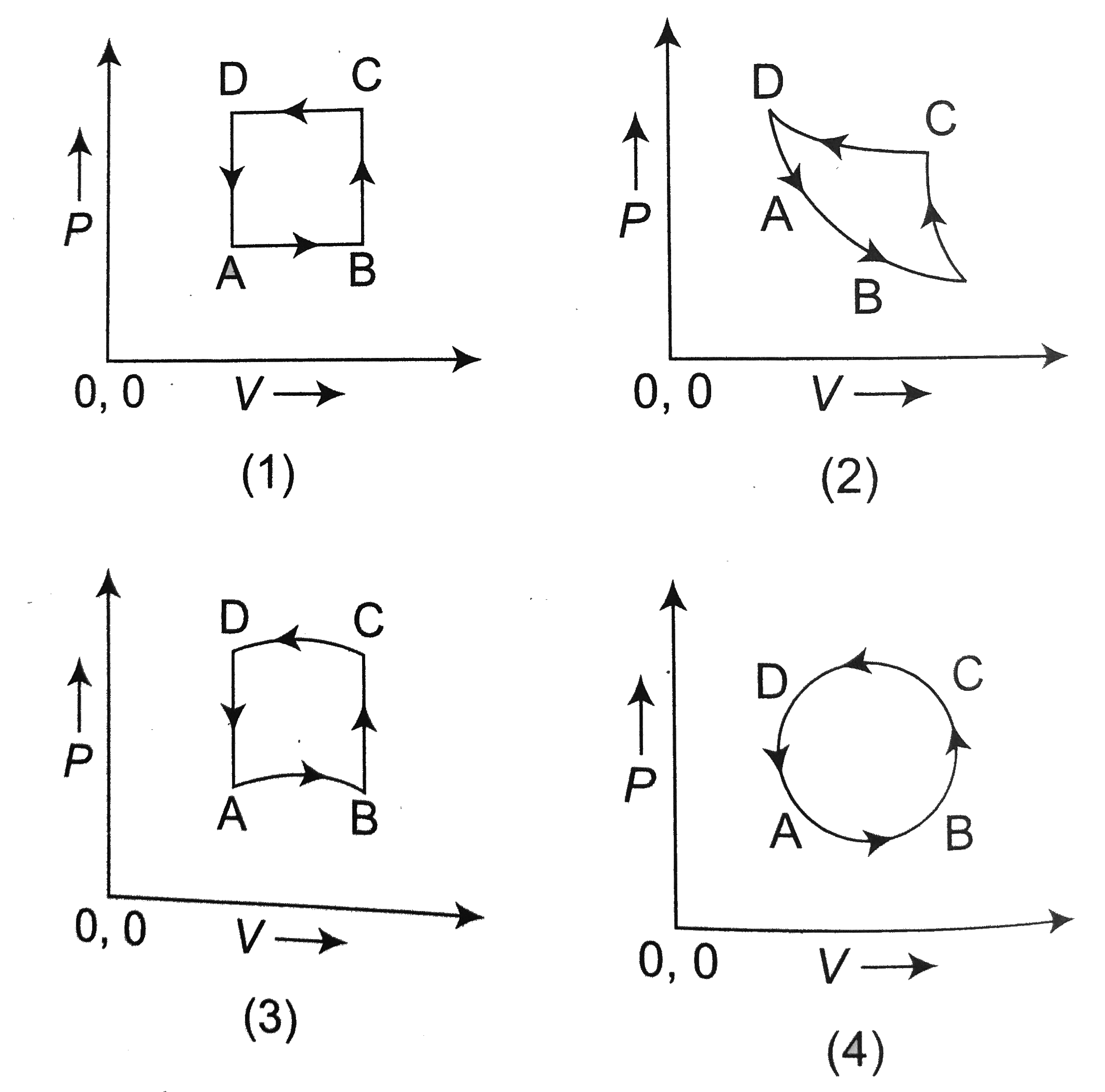
View SolutionIf the door of a refrigerator is kept open, then which of the following is true
View SolutionThe temperature of an ideal gas increases in an:
View SolutionFor two mole of an ideal gas :
View SolutionWhich of the following expressions is true for an ideal gas ?
View SolutionIf liquefied oxygen at 1 atmospheric pressure is heated from 50K to 300k by supplying heat at constant rate. The graph of temperature vs time will be
View SolutionFor a closed container containing `100` mol of an ideal gas fitted with movable, frictionless, weightless piston operating such that pressure of gas remain constant at `8.21` atm, which graph repsents correct variation of log `V v//s` log `T` where `V` is in litre and `T` is in Kelvin ? `(R = 0.0821 (atmL)/(molK))`
View Solution10 mole of ideal gas expand isothermally and reversibly from a pressure of `10atm` to `1atm` at `300K`. What is the largest mass which can lifted through a height of `100` meter?
View SolutionA heat engine carries one mole of an ideal monoatomic gas around the cycle as shown in the figure, the amount of heat added in the process AB and heat removed in the process CA are :
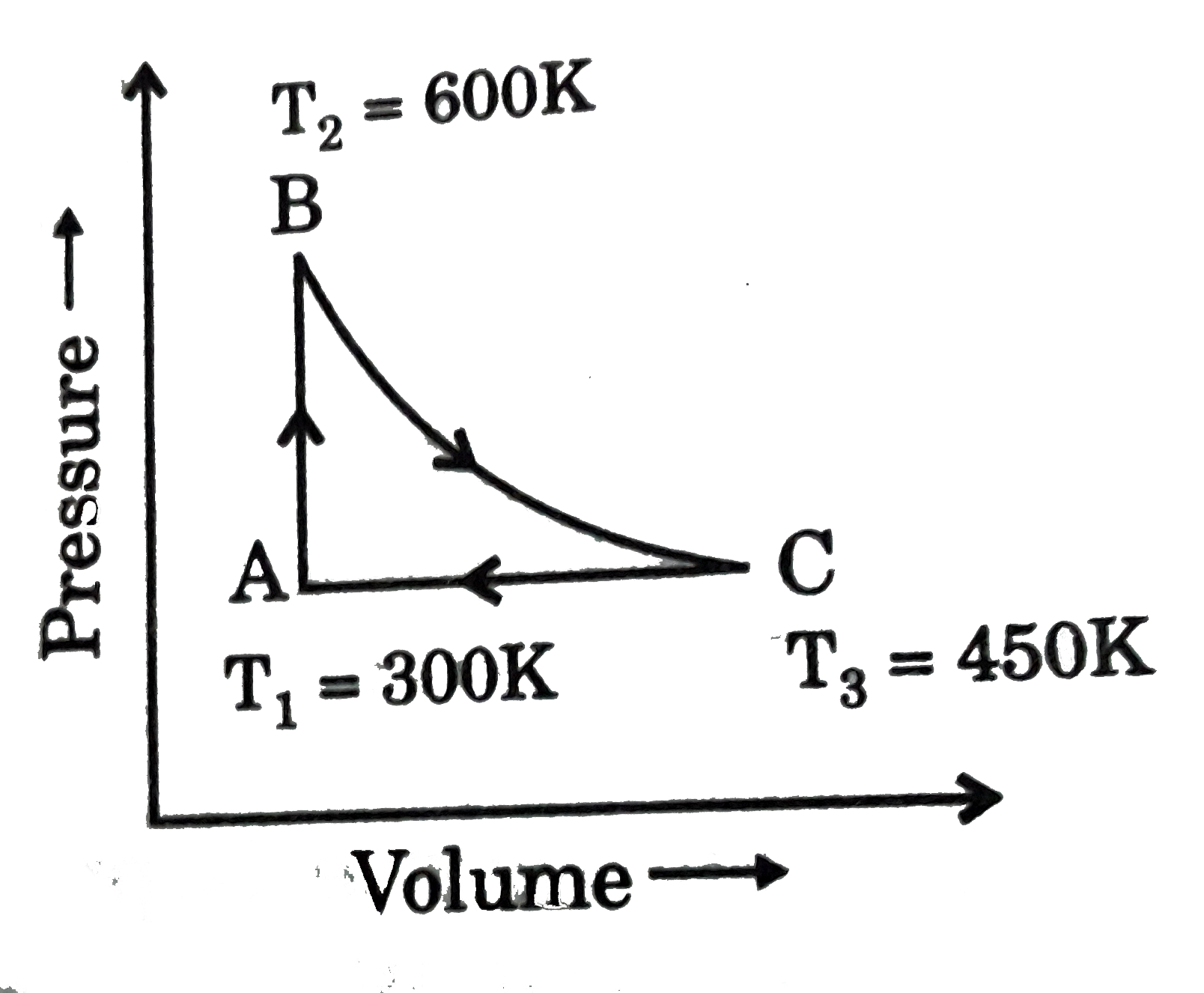
View SolutionWhat is the final temperature of `0.10` mole monoatomic ideal gas that performs `75 cal` of work adiabatically.if the initial temperature is `227 ^(@)C` ( use `R=2 cal //K-mol)`
View SolutionThe work done by `1` mole of ideal gas during an adiabatic process is (are ) given by :
View SolutionDuring an adiabatic process, the pressure of a gas is found to be proportional to the cube of its absolute temperature. The ratio `C_P//C_V` for the gas is
View SolutionA gas expands adiabatically at constant pressure such that `T propV^(-1//2)` The value of `gamma (C_(p,m)//C_(v,m))` of the gas will be :
View SolutionFor a reversible adiabatic ideal gas expansion `(dp)/(p)` is equal to
View Solution`P-V` plot for two gases (assuming ideal) during adiabatic processes are given in the figure. Plot `A` and Plot `B` should correspond respectively to:
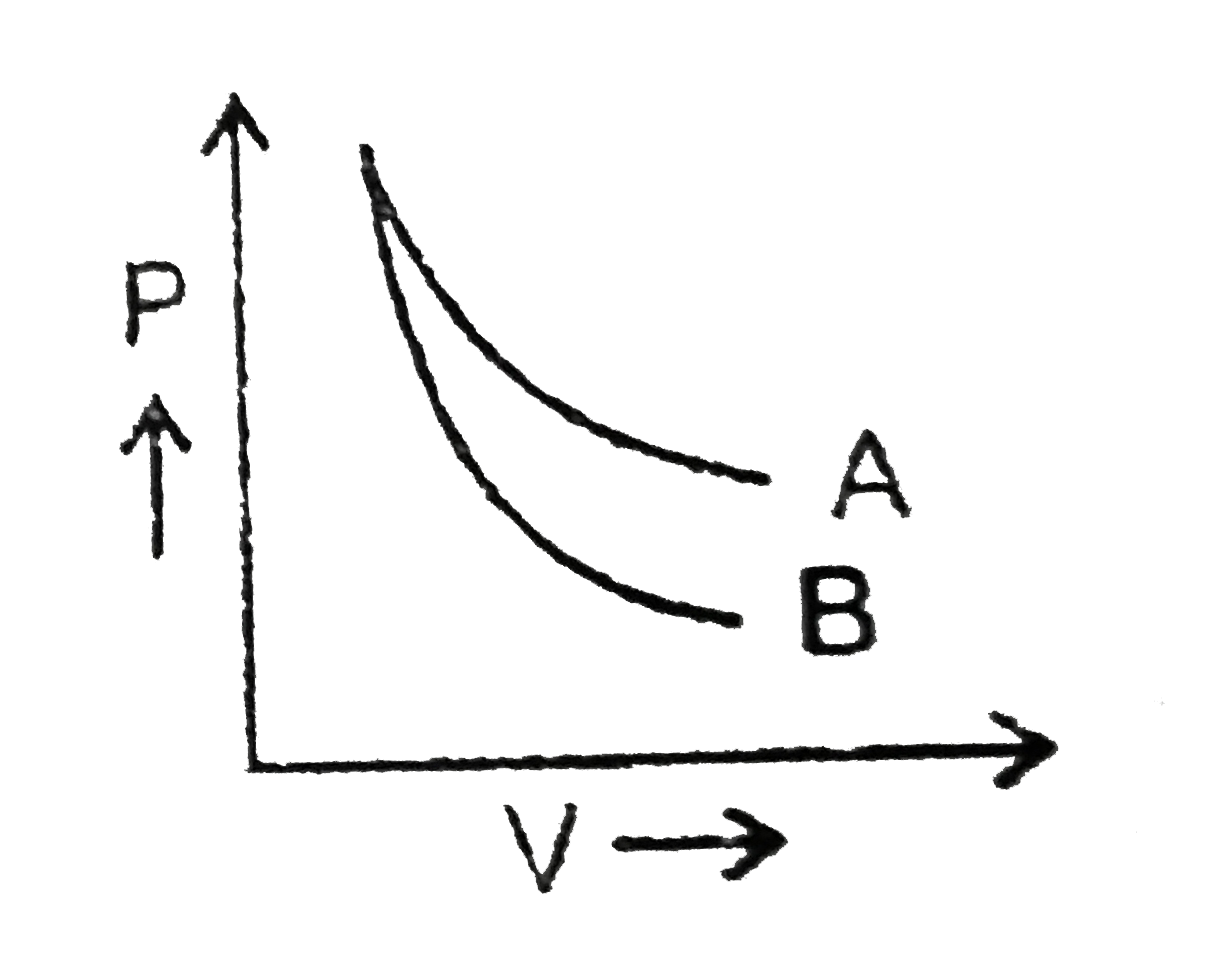
View SolutionCalculate the final temperature of a monoatomic idal gas that is compressed reversible and adiabatically from `16L` to `2L` at `300 K :`
View Solution5 mole of an ideal gas expand isothermally and irreversibly from a pressure of 10 atm to 1 atm against a constant external pressure of 1 atm. `w_(irr)` at 300 K is :
View SolutionWith what minimum pressure (in kPa), a given volume of an ideal gas `(C_(p,m)=7//2R)` originally at 400 K and 100 kPa pressure can be compressed irreversibly adiabatically in order to raise its temperature to 600 K :
View SolutionThe work done in adiabatic compression of `2` mole of an ideal monoatomic gas by constant external pressure of `2 atm` starting from initial pressure of `1 atm` and initial temperature of `30 K(R=2 cal//"mol-degree")`
View SolutionOne mole of an ideal gas `(C_(v,m)=(5)/(2)R)` at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View Solution10 litre of a non linear polyatomic ideal gas at `127^(@)C` and 2 atm pressure is suddenly released to 1 atm pressure and the gas expanded adiabatically against constant external pressure. The final temperature and volume of the gas respectively are.
View SolutionCalculate average molar heat capacity at constant volume of gaseous mixture contained 2 mole of each of two ideal gases `A(C_(v,m)=(3)/(2)R)` and `B(C_(v,m)=(5)/(2)R) :`
View Solution0.5 mole each of two ideal gases`A (C_(v,m)=(5)/(2)R)` and `B (C_(v,m)=3R)` are taken in a container and expanded reversibly and adiabatically, during this process temperature of gaseous mixture decreased from 350 K to 250 K. Find `DeltaH` (in cal/mol) for the process :
View SolutionA cyclic process `ABCD` is shown in the `P-V` diagram. Which of the following curves represents the same process?
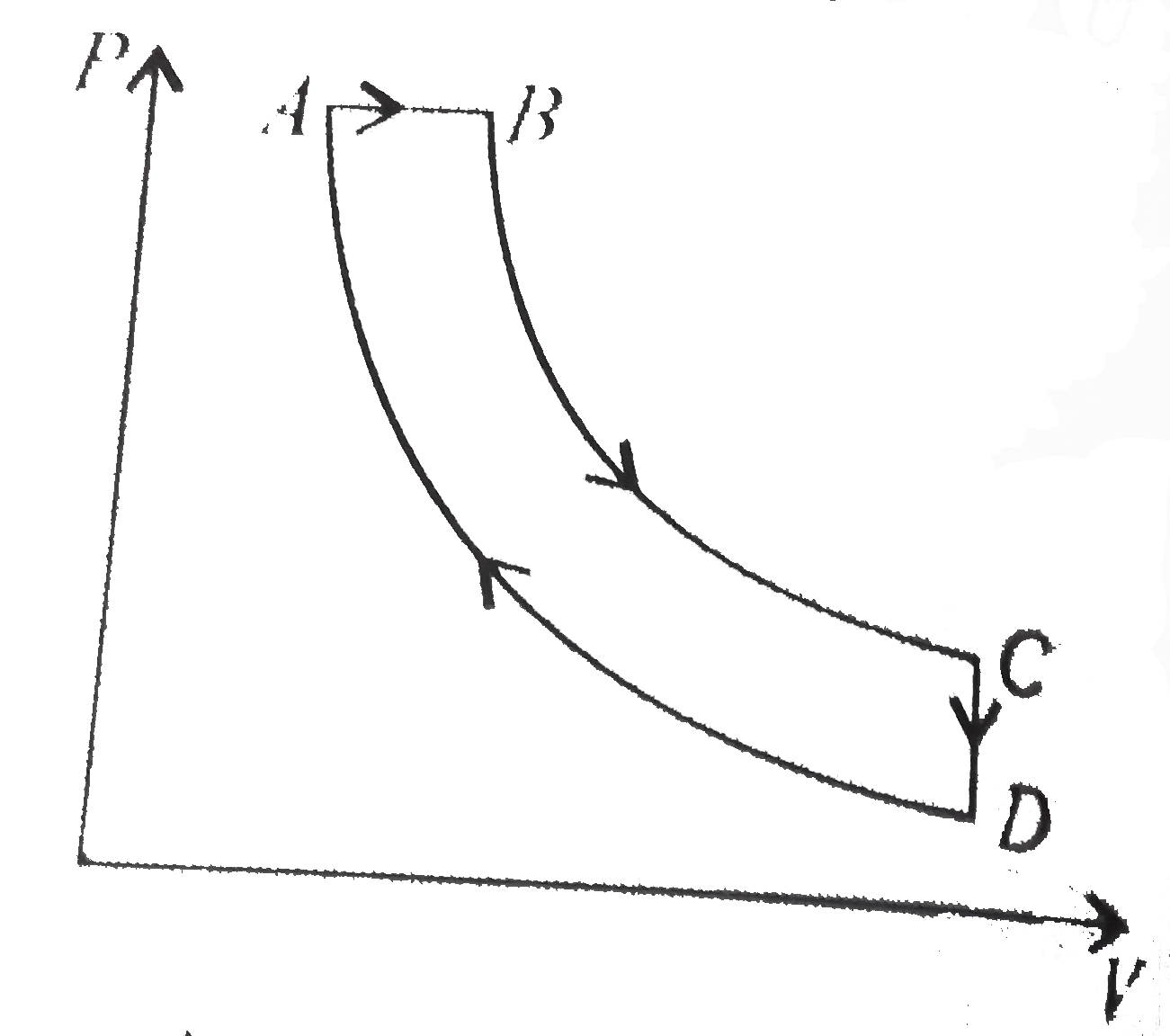
View Solution36 mL of pure water takes 100 sec to evaporate from a vessel when a heater of 806 watt is used. The `DeltaH_("vaporisation")` of `H_(2)O` is (density of water `=1g//c c)`
View SolutionFor the reaction : `PCl_(5) (g) rarrPCl_(3) (g) +Cl_(2)(g)`:
View SolutionConsider the reaction at 300 K
`H_(2)(g)+Cl_(2)(g)to2HCl(g), DeltaH^(@)=-185kJ`
If 2 mole of `H_(2)` compeletely react with 2 mole of `Cl_(2)` to form `HCl`. What is `DeltaU^(@)` for this reaction ?
View SolutionWhich of the indicated relationship is correct for the following exothermic reaction carried out at constant pressure?
`CO(g) +3H_(2)(g ) rarrCH_(4)(g)+H_(2)O(g)`
View SolutionOne mole of an ideal gas undergoes a change of state (2.0) atm, 3.0 L) to (2.0 atm, 7.0 L) with a change in internal energy `(DeltaU) = 30` L-atm. The change in enthalpy `(DeltaH)` of the process in L-atm :
View SolutionWhat is the change internal energy when a gas contracts from 377 mL to 177 mL under a constant pressure of 1520 torr, while at the same time being cooled by removing 124 J heat ?
`[Take :( 1 L atm ) =100 J)]`
View SolutionFor the real gases reaction,
`2CO(g)+O_(2)(g)to2CO_(2)(g),DeltaH=-560 kJ.` In 10 litre rigid vessel at 500 K the initial pressure is 70 bar and after the reaction it becomes 40 bar. The change in internal energy is :
View SolutionOne mole of non`-` ideal gas undergoes a change of state `(1.0 atm, 3.0L, 200 K )` to `(4.0 atm, 5.0L,250 K)` with a change in internal energy `(DeltaU)=40 L-atm`. The change in enthalpy of the process in `L-atm`,
View SolutionConsider the reacting at `300K`
`C_(6)H_(6)(l)+(15)/(2)O_(2)(l)rarr 6CO_(2)(g)+3H_(2)O(l),DeltaH=-3271`kJ
What is `DeltaU` for the combustion of `1.5` mole of benzene at `27^(@)C` ?
View SolutionFor the reaction , `FeCO_(3)(s)rarrFeO(s)+CO_(2)(g),DeltaH=82.8kJ` at `25^(@)C`, what is `(DeltaE " or "DeltaU)` at `25^(@)C`?
View SolutionAt `5xx10^(4)` bar pressure density of diamond and graphite are `3 g//c c` and `2g//c c` respectively, at certain temperature `'T'`.Find the value of `DeltaU-DeltaH` for the conversion of 1 mole of graphite to 1 mole of diamond at temperature `'T' :`
View SolutionPredict which of the following reaction `(s)` has a positive entropy change?
`I` . `Ag^(+)(aq)+Cl^(-)(aq)rarrAgCl(s)`
`II` . `NH_(4)Cl(s)rarrNH_(3)(g)+HCl(g)`
`III` . `2NH_(3)(g)rarrN_(2)+3H_(2)(g)`
View SolutionPredict which of the following reaction(s) has a negative entropy change?
`I. CH_(4)(g) +2O_(2)(g)rarrCO_(2)(g)+2H_(2)O(l)`
`II. NH_(3)(g)+HCl(g)rarrNH_(4)Cl(s)`
`III. 2KClO_(4)(s) rarr2KClO_(3)(s)+O_(2)(g)`
View SolutionWhich of the following reactions is asssociated with the most negative change in entropy?
View SolutionWhen two moles of an ideal gas `(C_(p.m.)=(5)/(2)R)` heated form 300K to 600K at constant pressure, the change in entropy of gas `(DeltaS)` is:
View SolutionWhich of the following expression for entropy change of an irreversible process ?
View SolutionWhich of the following expression is known as Clausius inequality ?
View SolutionIn a previous problem, calculate `DeltaS_(gas) ` If process is carried out at constant volume:
View SolutionIf one mole of an ideal gas `(C_(p.m.)=(5)/(2)R)` is expanded isothermally at 300K until it’s volume is tripled, then change in entropy of gas is:
View SolutionIf one mole of an ideal gas `C_p = 5/2 R` is expanded isothermally at 300 k until it's volume is tripled., if expansion is carried out freely `(P_(ext)=0), then DeltaS is :`
View SolutionWhen one mole of an ideal gas is compressed to half of its initial volume and simultaneously heated to twice its initial temperature, the change in entropy of gas `(DelataS)` is:
View SolutionWhat is the change in entropy when `2.5` mole of water is heated from `27^(@)C` to `87^(@)C`?
Assume that the heat capacity is constant `(C_(p))_(m)(H_(2)O)=4.2J//g=k,ln(1.2)=0.18)`
View SolutionCalculate standard entropy change in the reaction
`Fe_(2)O_(3)(s)+3H_(2)(g) rarr 2Fe(s)+3H_(2)O(l)`
Given `: S_(m_(0))(Fe_(2)O_(3).S)=87.4,S_(m)^(@)(Fe,S)=27.3`
`S_(m)^(@)(H_(2),g)=130.7,S_(m)^(@)(H_(2)O,l)=69.9JK^(-1)mol^(-1)`
View SolutionCalculate the entropy change `(J//mol K)` of the given reaction. The molar entropies `(J//K-mol)` are given in brackets after each substance:
`2PbS(s)[19.2]+3O_(2)(g)[205.1]`
` to 2PbO(s)[66.5]+2O_(2)(g)[248.2]`
View SolutionGiven `Delta_(r)S^(@)=-266` and the listed `[S_(m)^(@)value]` Calculate `S^(@) "for" Fe_(3)O_(4)(s)`
`4Fe_(3)O_(4)(s)[...] +O_(2)(g)[205] to6Fe_(2)O_(3)(s)[87]`
View SolutionThe entropy change for a phase transformation is :
View SolutionWhat is the melting point of benzene if `DeltaH_("fusion")= 9.95kJ//mol` and `DeltaS_("fusion")= 35.7J//K-"mol"`
View Solution`DeltaS` for freezing of 10 g of `H_(2)O(l)` (enthalpy of fusion is 80 cal/g) at `0^(@)C` and 1 atm is :
View SolutionChloroform has `DeltaH_("vaporization")=29.2 kJ//"mol"` and boils at `61.2^(@)C`. What is the value of `DeltaH_("vaporization")=29.2 kJ//"mol"` for chloroform ?
View SolutionThe entropy if vaporisation of benzene is `85JK^(-1) mol^(-1)`. When 117g benzene vaporizes at its's normal boiling point, the entropy change in surrounding is:
View SolutionIdentify the correct statement regarding entropy
View SolutionCalculate `DeltaS` for following process :
`underset("at" 100K)(X(s)) underset("at" 200 K)(rarrX(l))`
Given : Melting point of `X_(s)=100K,DeltaH_("Fusion")=20kJ//"mol",C_(p.m)(X,l)=10J//"mol".K`
View SolutionFor a perfectly crystalline solid `C_(p.m.)=aT^(3)`, where ais constant. If `C_(p.m.)` is 0.42.J//K-"mol" at 10K, molar entropy at 10K is:
View SolutionConsider the following spontaneous reaction `3X_(2)(g)rarr2X_(3)(g)`. What are the sign of `DeltaH`, `DeltaS` and `DeltaG` for the reaction ?
View SolutionFor the reaction `2H(g)rarr H_(2)(g)`, the sign of `DeltaH` and `DeltaS` respectively are :
View SolutionConsider the following reaction.
`C_(6)H_(6)(l)+(15)/(2)O_(2)(g)rarr6CO_(2)(g)+3H_(2)O(g)`
signs of `DeltaH, DeltaS` and `DeltaG` for the above reaction will be
View SolutionConsider the following reaction at temperature T :
`CH_(2)=CH_(2)(g) +Cl_(2)(g)rarrClCH_(2)CH_(2)Cl(g)`
`Delta_(r ) H^(@)=-217.5kJ//"mol, " Delta_(r )S^(@)=-233.9J//K-"mol"`
Reaction is supported by :
View SolutionFor a process to be spontaneous, `DeltaG` must be………… .
View SolutionFor a reaction to occur spontaneously
View SolutionWhich of the following conditions reagarding a chemical process ensures its spontaneity at all temperature?
View SolutionThe free energy change `DeltaG = 0`, when
View SolutionWhich of the following conditions may lead to a non-spontaneous change?
View SolutionSuppose that a reaction has `DeltaH=-40kJ` and `DeltaS =- 50J//K`. At what temperature range will it change from spontaneous to non-spontaneous?
View SolutionFor isothermal expansion in case of an ideal gas `:`
View SolutionWhat is the normal boiling point of mercury?
Given : `DeltaH _(f)^(@)(Hg,l)=0,S^(@)(Hg,l)=77.4 J//K-"mol"`
`DeltaH _(f)^(@)(Hg,g)= 60.8 kJ//"mol", S^(@)(Hg, g)=174.4 J//K-"mol"`
View Solution19 gm of ice is converted into water at `0^(@)C` and 1 atm. The entropies of `H_(2)O(s)` and `H_(2)O(l)` are 38.2 and `60 J//"mol " K` respectively. The enthalpy change for this conversion is :
View SolutionUsing the listed [`DeltaG_(f)^(@)` values] calculate `DeltaG^(@)` for the reaction :
`3H_(2)S(g)[-33.6] +2HNO_(3)(l)[-80.6]rarr2NO(g)[+86.6]+4H_(2)O(l)[-237.1]+3S(s)[0.0]`
View SolutionFrom the following `DeltaH^(@)` and `DeltaS^(@)` values, predict which of reactions I, II and III would be spontaneous at `25^(@)C`.
`{:(,DeltaH^(@)(kJ),,DeltaS^(@)(J//K),),(I.,+10.5,,+30,),(II.,+1.8,,-113,),(III.,-126,,+84,):}`
View SolutionCalculate `DeltaH_(f)^(@)` for `Ubr_(4)` from the `DeltaG^(@)` of reaction and the `S^(@)` values at 298 K.
`U(s)+2Br_(2)(l)rarrUBr_(4)(s), DeltaG^(@)=-788.6 kJ. " "S^(@)(J//K-"mol")50.3, 152.3, 242.6`
View SolutionThe entropies of `H_(2)` (g) and H (g) are 130.6 and 114.6 J `mol^(-1)K^(-1)` respectively at 298 K. Using the data given below calculate the bond energy of `H_(2)` (in kJ/mol) :
`H_(2)(g)rarr2H(g),DeltaG^(@)=406.6kJ`
View SolutionConsider the `DeltaG_(f)^(@)` and `DeltaH_(f)^(@)` (kJ`//`mol) for the following oxides. Which can be most easily decomposed to form the metal and oxygen gas?
View SolutionWhich of the following option is correct ?
View SolutionCalculate `DeltaG^(@)` (kJ/mol) at `127^(@)C` for a reaction with `K_("equilibrium")=10^(5)` :
View SolutionWhen reaction is at standard state at equilibrium, then
View SolutionFor the auto-ionization of water at `25^(@)C, H_(2)O(l)iff H^(+)(aq)+OH^(-)` (aq) equilibrium constant is `10^(-14)`.
What is `DeltaG^(@)` for the process?
View SolutionHess's law states that
View SolutionAn imaginary reaction `X rarr Y` takes place in three steps
`X rarr A, DeltaH=-q_(1), " "BrarrA, DeltaH=-q_(2), " "BrarrY, DeltaH=-q_(3)`
If Hess's law is applicable, then the heat of the reaction `(X rarr Y)` is :
View SolutionThe enthalpy change for a reaction does not depend upon:
View Solution
Exercise questions and complete solutions for chapter THERMODYNAMICS of NARENDER AVASTHI CHEMISTRY (HINGLISH) of Class 11