Complete Solutions to बहुविकल्पीय प्रश्न of chapter सरल रेखा में गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | सरल रेखा में गति |
| NAVBODH PARIKSHA SAAR | बहुविकल्पीय प्रश्न |
| Number Of Questions | 55 |
| Academic Year | 2023-24 |
यदि एक वस्तु एक लकड़ी के ब्लॉक में 3 सेमी भेदन करने पर आधा वेग खो देती है तो रुकने के पहले वः कितना और भेदन करेगी -
View Solutionकिसी समय t पर किसी गतिमान कण के निर्देशांक `x=alpha t^(3)` तथा `y=betat^(3)` हैं। समय t पर कण की चाल होगी -
View Solutionकोई गेंद किसी h मीटर ऊँचाई की मीनार की चोटी से गिरायी जाती है तथा वह भूमि तक पहुँचने में T सेकण्ड का समय लेती है। `(T)/(3)` सेकण्ड पश्चात गेंद की स्थिति क्या है -
View Solutionसमय t तथा दुरी x के बीच संबंध को `t=ax^(2)+bx` द्वारा व्यक्त किया जाता है, जहाँ a और b नियतांक हैं। यहाँ त्वरण है -
View Solutionकोई कार विराम से गति प्रारंभ करके s दुरी तक f की दुरी से त्वरित होती है । तत्पश्चात t समय तक नियत चाल से चलती है और फिर `(f)/(2)` की दर से मंदित होकर विराम में आ जाती है। यदि कार द्वारा चली गई कुल दुरी 15s है, तो -
View Solutionx = 0 पर स्थित एक कण समय t = 0 से धनात्मक x दिशा में v वेग से गतिमान है, जहाँ `v=a sqrtx` है। कण का विस्थापन समय के साथ इस प्रकार परिवर्तित होता है -
View Solutionएक कण का वेग `v=u+g t+ft^(2)` है। यदि `t = 0` पर कण की स्थिति `x=0`, तो `t=1` सेकण्ड पर विस्थापन होगा -
View Solutionएक वस्तु समय `t = 0` पर विराम में है। वह X - अक्ष की धन दिशा में एक नियम त्वरण से गति प्रारंभ करती है । ठीक उसी समय X - अक्ष धन दिशा में के नियम चाल से गति करती हुई दूसरी वस्तु `X = 0` से गुजरती है। समान समय t के बाद पहली वस्तु की स्थिति `x_(1)(t)` तथा दूसरी वस्तु की स्थिति `x_(2)(t)` से प्रदर्शित की जाती है। निम्नलिखित में से कौन- सा ग्राफ `(x_(1)-x_(2))` को समय t के फलन के रूप में सत्य प्रदर्शित करता है -
View Solutionचित्र में दो घर्षण रहित नत समतल क्षैतिज में क्रमशः `60^(@)` और `30^(@)` के कोण बनाते हुए प्रदर्शित किए गए हैं। इन तलों पर दो ब्लॉक A और B रखे जाते हैं। A का B के सापेक्ष ऊर्ध्वाधर त्वरण होगा -

View Solution6.25 मीटर/सेकण्ड की चाल से गतिशील एक वस्तु के मंदन की दर इससे दी जाती है `(dv)/(dt)=-2.5sqrtv` जहाँ v तात्क्षणिक चाल है। वस्तु को विरामावस्था में आने में लगा समय है -
View Solutionऊँचाई H की एक मीनार से एक कण को चाल u से ऊर्ध्वाधर ऊपर की और फेंका जाता है। कण को पृथ्वी तक गिरने में लगा समय उसके उच्चतम बिंदु तक पहुँचने के समय का n गुना है। H, u और n के बीच संबंध है-
View Solutionकिसी 240 मीटर ऊँची चोटी के एक किनारे से दो पत्थरों को एक साथ ऊपर की ओर फेंका जाता है। इनकी प्रारम्भिक चाल 10 मी/से तथा 40 मी/से है।
निम्नलिखित में से कौन-सा ग्राफ पहले पत्थर के सापेक्ष दूसरे पत्थर की स्थिति के समय विचरण को सर्वाधिक सही दर्शाता है -
View Solutionएक पिंड ऊर्ध्वाधर ऊपर की ओर फेंका जाता है। निम्न में से समय के साथ वेग का सही ग्राफ है -
View Solutionएक कण एक सरल रेखा के अनुदिश इस प्रकार गति करना है कि किसी समय t पर इसका विस्थापन है -
`s=3t^(3)+7t^(2)+14t+5`
t = 1 सेकंड पर कण का त्वरण है -
View Solutionएक गेंद को u चाल से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है, तो इसके चढ़ाव के अंतिम t सेकंडों में इसके द्वारा तय की की गई दुरी होगी -
View Solutionएक व्यक्ति प्रत्येक 2 सेकंड में अंतराल पर गेंदों को आकाश में उर्ध्वाधरत: फेंकता है । गेंदों की चाल कितनी होनी चाहिए कि एक समय में आकाश में 2 से अधिक गेंदें हों `(g=9.8" m/s"^(2))`-
View Solutionदो पिंडो A (द्रव्यमान 1 किग्रा ) ओर B (द्रव्यमान 3 किग्रा ) को क्रमानुसार ऊँचाइयों 16 मीटर और 25 मीटर से छोड़ा गया है। इनके पृथ्वी तल तक पहुँचने के क्रमागत समयों का अनुपात होगा -
View SolutionX - अक्ष पर किसी कण का समय t के संदर्भ में निर्धारित स्थान x समीकरण `x=9t^(2)-t^(3)` द्वारा व्यक्त किया जा सकता है, जब x मीटर में तथा t सेकंड में है । `+x` दिशा में कण का स्थान क्या होगा जब उसकी चाल उच्चतम होगी -
View Solutionएक मोटर गाड़ी X से y तक अचर चाल u से चलती है तथा Y से X तक अचर चाल v से वापस लौटती है। इस पूरी यात्रा के लिए गाड़ी की औसत चाल होती -
View Solutionएक कण विराम अवस्था से प्रारंभ कर `(4)/(3)` मीटर/सेकंड^2 के त्वरण से गतिमान है। विराम अवस्था से तीसरे सेकंड में वह कितनी दूर चलेगा -
View Solutionचित्र में एक कण के लिए दुरी - समय वक्र प्रदर्शित किया गया है। इसका अधिकतम तात्क्षणिक वेग वक्र के किस बिंदु के आसपास होगा -
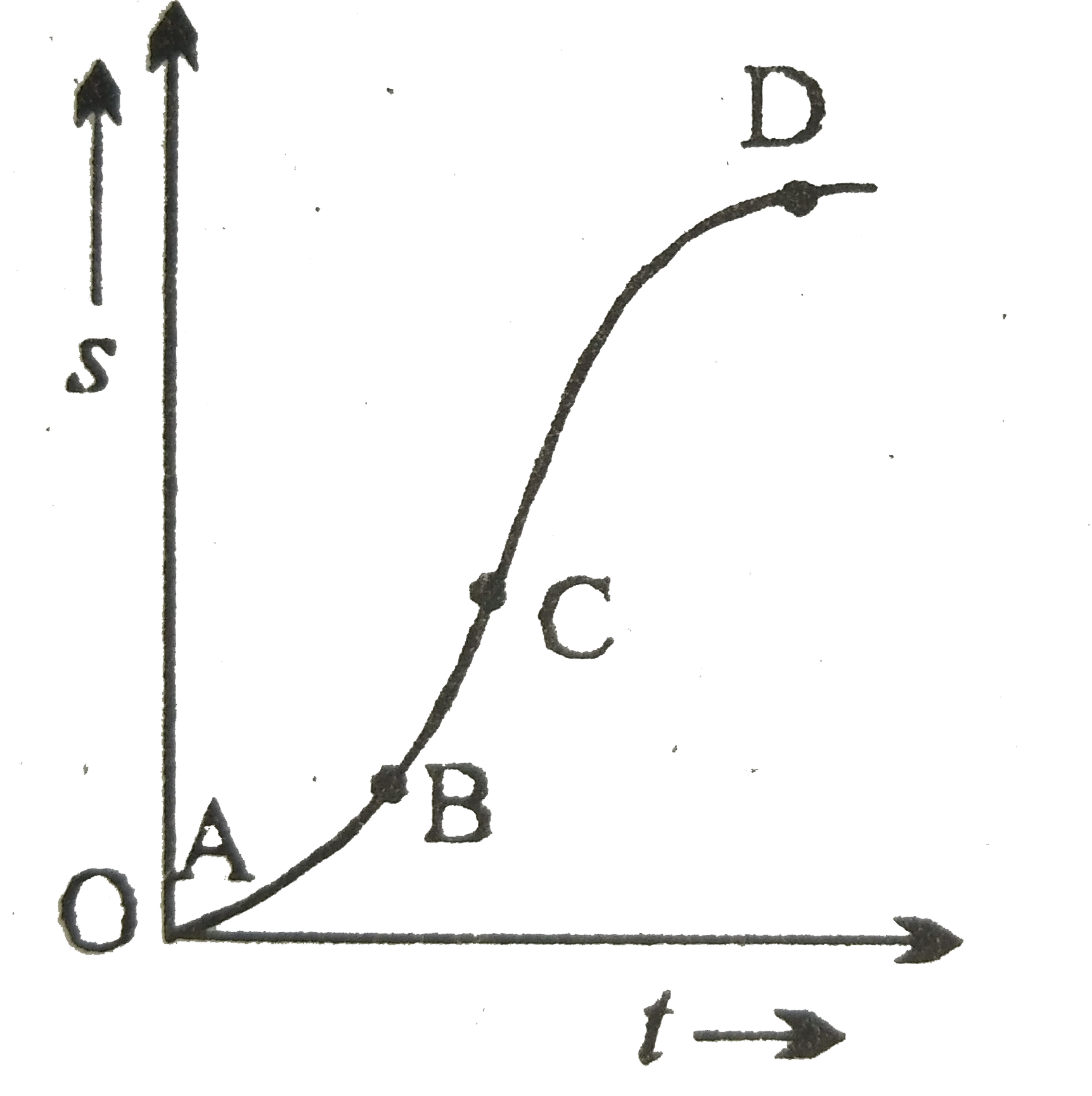
View Solutionएक कण अचर त्वरण से एक सीधी रेखा पर चल रहा है। गति पथ में एक स्थान पर t सेकंड में 135 मीटर की दुरी चलने पर इसका वेग 10 मीटर/सेकंड से 20 मीटर/सेकंड हो जाता है। t का मान होगा -
View Solutionएक कण एक नियत बल की क्रिया के अंतर्गत विरामावस्था से गति प्रारंभ करता है। यदि पहले 10 सेकंड में तय की गई दुरी `s_(1)` है तथा पहले 20 सेकंड में तय की गई दुरी `s_(2)` है। तब
View Solutionएक गेंद विरामावस्था से t = 0 समय पर ऊँचे उठे प्लेटफार्म से छोटी जाती है ओर इसके 6 सेकंड बाद उसी प्लेटफार्म से एक अन्य गेंद चाल v से नीचे की ओर फेंकी, जाती है। दोनों गेंदें 18 सेकंड बाद मिलती हैं। तब v का मान होगा -
`(g=10" मी/से"^(2))`
View Solutionवेग से एक कण इसकी आधी दुरी तय करती है तथा शेष आधी दुरी `v_(2)` वेग से तय करता है। पूरी यात्रा के दौरान इसकी औसत चाल होगी -
View Solutionएक सरल रेखा के अनुदिश किसी कण की गति समीकरण `x=8+12t-t^(3)` के द्वारा प्रदर्शित की जाती है, जहाँ x मीटर में तथा t सेकंड में है। वेग शून्य होने पर मंदन होगा -
View Solutionएक पत्थर मुक्त अवस्था में गुरुत्व के अंतर्गत गिराया जाता है। पहले 5 सेकंड में `h_(1)`, दूसरे 5 सेकंड में `h_(2)` तथा तीसरे पांच सेकंड `h_(3)` में दुरी तय करता है। `h_(1), h_(2)` ओर `h_(3)` में संबंध होगा -
View Solutionदो कार P ओर Q एक ही क्षण पर के बिंदु से एक सरल रेखा में चलना प्रारंभ करती है। किसी क्षण t पर उनकी स्थितियाँ `x_(p)(t)=at+bt^(2)` तथा `x_(Q)(t)=ft-t^(2)` हैं। दोनों कारों के वेग समान होने का समय होगा -
View Solutionएक दिन मैट्रों स्टेशन पर गतिमान सीढ़ी के न चलने पर प्रीति उसकी सीढ़ियों पर पैदल ऊपर चढ़ती है। इसमें उसे `t_(1)` समय लगता है। अन्य दिनों में जब गतिमान सीढ़ी कार्यशील होती है तब वह खड़ी रहकर `t_(2)` समय में ऊपर पहुँच जाती है। उसके द्वारा सीढ़ियों पर चलकर ऊपर चढ़ने में लिया गया समय होगा -
View Solutionसरल रेखा में गतिमान एक पिंड का वेग-समय ग्राफ निम्न चित्र में दर्शाया गया है। 6 s में पिंड का विस्थापन तथा तय की गई दुरी होगी क्रमशः -
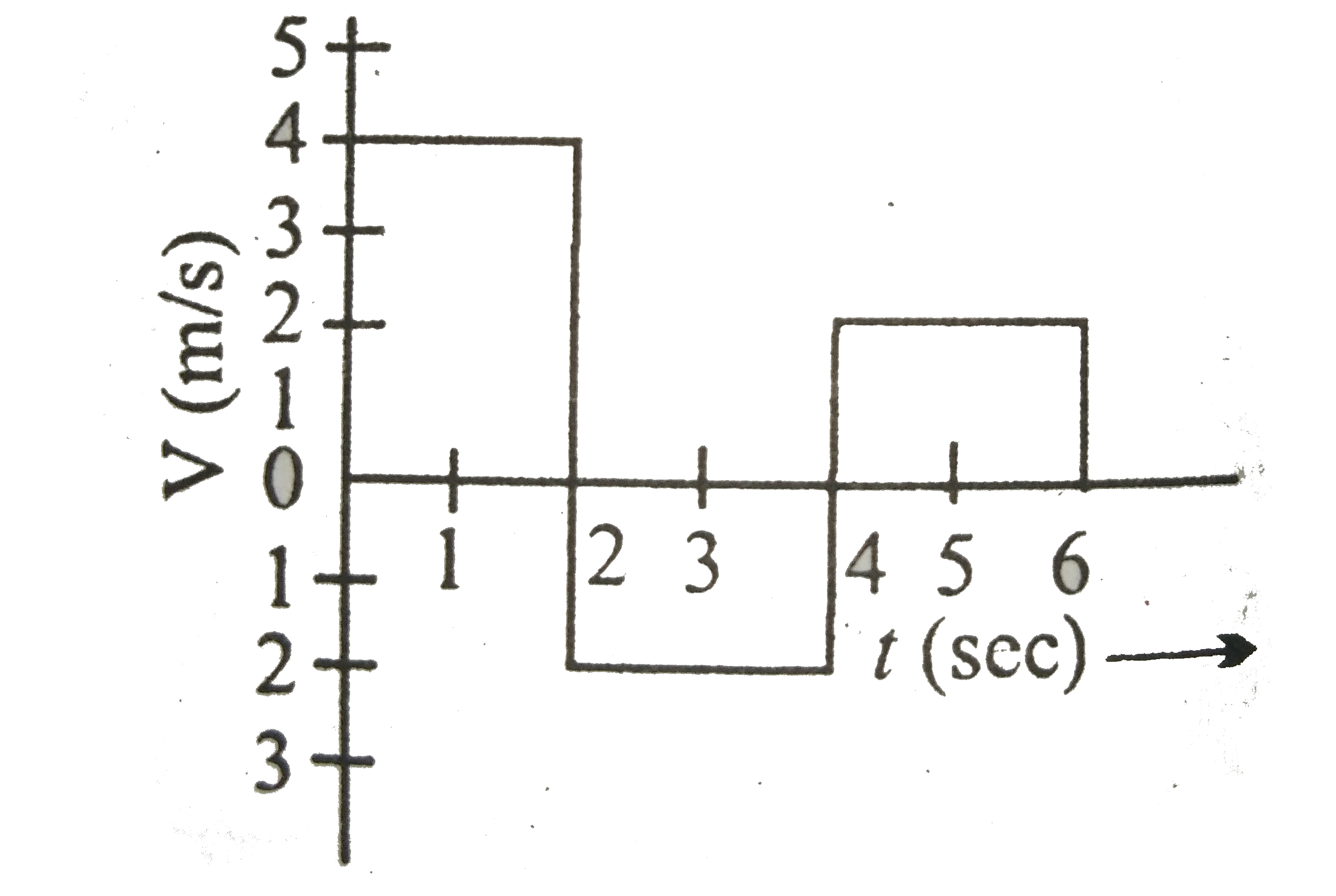
View Solutionएक वस्तु गुरुत्वीय क्षेत्र में स्वतंत्रतापूर्वक गिरना प्रारंभ करती है। उसके द्वारा प्रथम, द्वितीय व तृतीय सेकंड में तय की हुई दूरियों का अनुपात होगा -
View Solutionनीचे दर्शाए वेग-समय ग्राफ के लिए अंतिम दो सेकंड में पिंड द्वारा तय की गई, पुरे सात सेकंड में पिंड द्वारा तय की गई दुरी का कौन-सा भाग होगा -
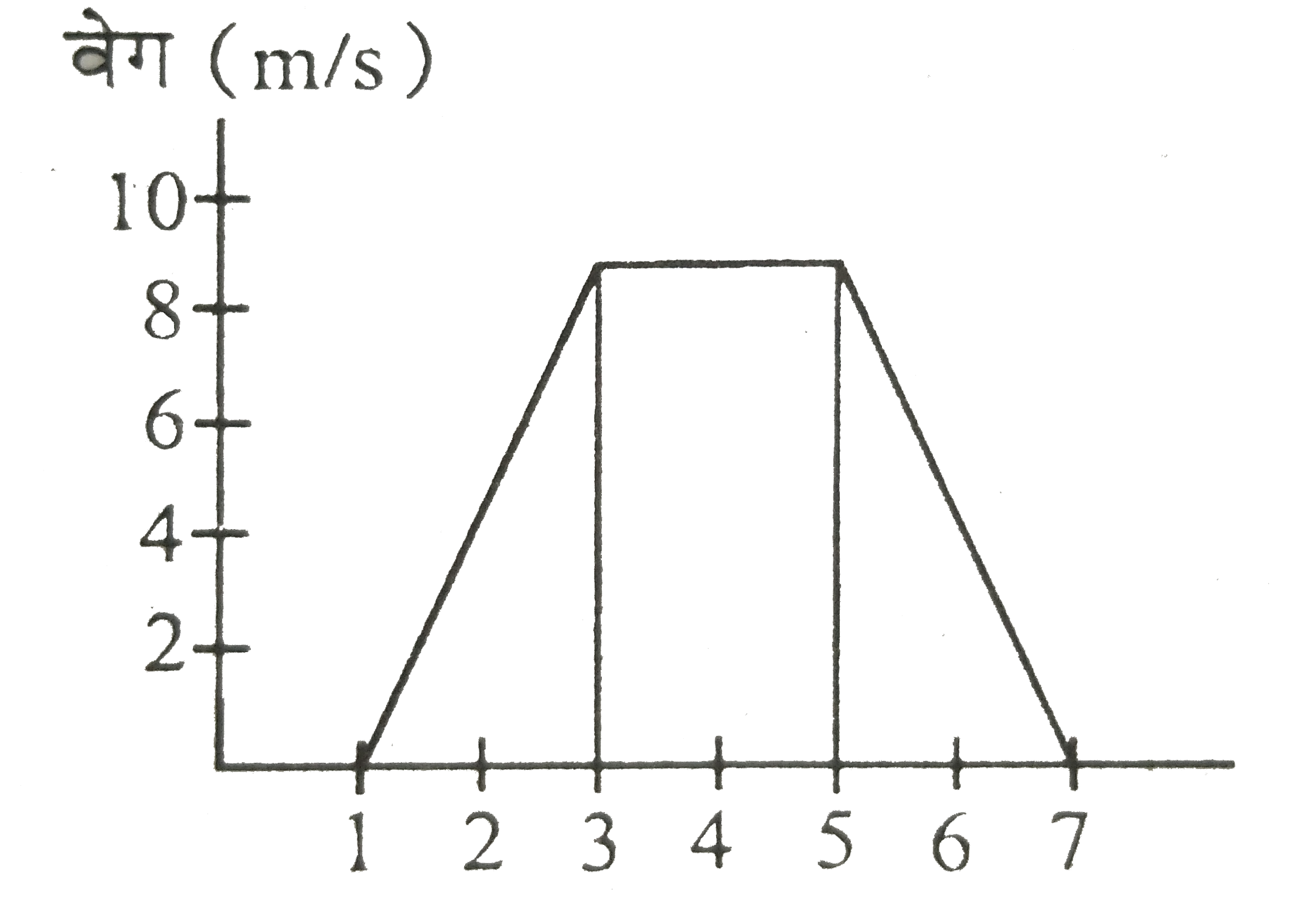
View Solutionदो कणों A तथा B के विस्थापन - समय ग्राफ समय अक्ष से क्रमशः `30^(@)` तथा `60^(@)` के कोण बनती हुई सरल रेखाएँ हैं। यदि A का वेग `v_(A)` तथा B का वेग `v_(B)` है तो `v_(A)//v_(B)` का मान होगा -
View Solutionएक स्थिर बल F के अनुप्रयोग से 10 m /s के वेग से चलती हुई कार को 20 m की दुरी में रोका जा सकता है। यदि कार का वेग 30 m /s हो तो इस बल के द्वारा कार को निम्न दुरी पर रोका जा सकता है -
View Solutionएक व्यक्ति अपनी यात्रा की आधी दुरी, `v_(1)` चाल से तथा शेष आधी दुरी `v_(2)` चाल से तय करता है। व्यक्ति की माध्य चाल होती -
View Solutionकिसी वस्तु के औसत वेग तथा औसत चाल के आंकिक मानों का अनुपात होता है सदैव -
View Solutionयदि कोई वस्तु पहली आधी दुरी `v_(1)` वेग से तथा दूसरी आधी दुरी `v_(2)` वेग से तय करती है, तो वस्तु का औसत वेग के लिए, सूत्र होगा -
View Solutionशून्य प्रारम्भिक वेग ओर एकसमान त्वरण a के साथ एक पिंड A चलता है। उसी बिंदु से दूसरा पिंड B उसी दिशा में एकसमान वेग v से चलता है। ये दोनों पिंड कितने समय के पश्चात मिलेंगे -
View Solutionएक कार समय t = 0 से शुरू होकर सीधे रस्ते पर नियत त्वरण a से t = T तक चलती है। उसके बाद नियत मंदन से कार स्थिर स्थिति में लायी जाती है। इस प्रक्रिया में कार की औसत चाल होगी -
View Solutionएक गेंद उर्ध्व दिशा में फेंके जाने पर T समय में अधिकतम ऊँचाई h पर पहुँचती है । T / 2 समय के बाद उसकी ऊँचाई होगी -
View Solutionएक कण को कुछ ऊँचाई से नीचे छोड़ा गया । इसके द्वारा क्रमशः `1-1m` की दुरी तय करने में लगा समय होगा -
View Solutionजब कोई कण कुछ समय के लिए गति में है तो निम्नलिखित में से क्या शून्य नहीं हो सकता है-
View Solutionएक पत्थर किसी ऊँचाई से गिराया जाता है और यह पत्थर ऊँचाई का `(5)/(9)`वाँ भाग अंतिम s में तय करता है। पत्थर को गिरने में लगा समय होगा -
View Solutionएक छोटा पिंड बिना घर्षण के एक झुके हुए तल पर विराम से गति करना प्रारंभ करता है । यदि `S_(n),` समय `t=n-1` से `t=n` में चली गयी दुरी हों तब `S_(n)` तथा `S_(n+1)` का अनुपात होगा -
View Solution9m ऊँची इमारत की छत से पानी की बूंदें नियमित समयांतराल में गिर रही हैं। जिस समय पहली बून्द जमीन पर पहुँचती है ठीक उसी समय चौथी बूँद गिरना प्रारंभ करती है। दूसरी और तीसरी बूँदों की छत से दूरियाँ होंगी -
View Solutionदो वस्तुऐं एक ही ऊँचाई से N s के समयांतराल में स्वतंत्रतापूर्वक गिरना प्रारंभ करती है। यदि पहली वस्तु के गिरना प्रारंभ करने के n s के पश्चात उनके बीच का ऊर्ध्वाधर अंतराल 1 हो, तो n निम्न के बराबर होगा -
View Solutionएक गेंद h m ऊँची मीनार की चोटी से v वेग से ऊर्ध्वाधर ऊपर की और फेंकी जाती है। गेंद निम्न समय के पश्चात जमीन से टकरायेगी-
View Solutionएक गुब्बारा वेग v से नीचे उतर रहा है। उससे एक गेंद वेग u से ऊर्ध्वाधर ऊपर की और फेंकी जाती है । गेंद गुब्बारे को निम्न समय के पश्चात पर करेगी -
View Solutionएक बहुमंजिली इमारत की 9 वीं मंजिल से गिरायी गयी गेंद 3 s में पृथ्वी पर पहुँचती है। स्वतंत्रतापूर्वक पतन के पहले s में यह n मंजिलों को पर करती है। n का मान होगा `(g=10m//s^(2))`-
View SolutionA ,B ,C और D किसी ऊर्ध्वाधर रेखा पर चार बिंदु इस प्रकार हैं कि `AB = BC = CD` एक वस्तु बिंदु A पर विरामावस्था में स्वतंत्रतापूर्वक गिरती है। तब AB ,BC और CD तक गिरने में लगे अंतराल निम्न अनुपात में होंगे -
View Solutionकोई वस्तु विरामावस्था में एकसमान त्वरण से चलना प्रारंभ करती है। पहले `(p-1) s` में उसका विस्थापन `s_(1)` तथा पहले `p s` में उसका विस्थापन `s_(2)` है। अतः `(p^(2)-p+1)` वें s में विस्थापन होगा -
View Solutionएक वस्तु जो एकसमान त्वरण से गतिमान है, दो बिंदुओं A और B को क्रमशः`20m//s` एवं `30m//s` के वेग से पार करती है। A और B के मध्य बिंदु पर उसकी चाल होगी -
View Solutionएक रेलगाड़ी नियत त्वरण से गतिमान है। इसके दोनों सिरे किसी बिंदु को क्रमशः u और v वेग से पार करते हैं। उसी बिंदु को रेलगाड़ी का मध्य बिंदु निम्न वेग से पार करेगा -
View Solutionदो कार A और B एक ही दिशा में वेग `v_(A)` और `v_(B)(v_(A)gt v_(B))` से गतिमान हैं। जब कार A कार B से s दुरी पीछे होती है तो कार A का चालक ब्रेक लगाता है जिससे कार A में एकसमान मंदन a उत्पन्न हो जाता है। दोनों में टक्कर नहीं होती यदि -
View Solutionएकांक द्रव्यमान का कोई कण एकविमीय गति करता है और इसका वेग समीकरण `v(x)=betax^(-2n)` के अनुसार परिवर्तित होता है, जहाँ `beta` और n नियतांक हैं तहत x कण की स्थिति है। इस कण के त्वरण को x के फलन के रूप में निरूपित किया जा सकता है -
View Solution
बहुविकल्पीय प्रश्न questions and complete solutions for chapter सरल रेखा में गति of NAVBODH PHYSICS (HINDI) of Class 11
All Exercises from NAVBODH PARIKSHA SAAR Class 11 PHYSICS सरल रेखा में गति
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर
- अभ्यासार्थ प्रश्न (अति लघु उत्तरीय प्रश्न/एक शब्द/एक वाक्य )
- अभ्यासार्थ प्रश्न (उचित संबंध जोड़िए - )
- अभ्यासार्थ प्रश्न (दीर्घ उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (मूल्य आधारित प्रश्न )
- अभ्यासार्थ प्रश्न (रिक्त स्थानों की पूर्ति कीजिए - )
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (वस्तुनिष्ठ प्रश्न ) (बहुविकल्पीय प्रश्न )
- अभ्यासार्थ प्रश्न (सत्य/असत्य लिखिए - )
- आंकिक उदाहरण
- आंकिक उदाहरण प्लस
- आंकिक प्रश्न
- उदाहरण
- तथ्यात्मक प्रश्न
- प्रश्नावली 3.1
- प्रश्नावली 3.2
- बहुविकल्पीय प्रश्न
- बोधात्मक प्रश्न
- बोधात्मक प्रश्न प्लस