Complete Solutions to बहुविकल्पीय प्रश्न of chapter कार्य, ऊर्जा और शक्ति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | कार्य, ऊर्जा और शक्ति |
| NAVBODH PARIKSHA SAAR | बहुविकल्पीय प्रश्न |
| Number Of Questions | 80 |
| Academic Year | 2023-24 |
6 मी/से की क्षैतिज चाल से चलता हुआ एक m द्रव्यमान का कण, उसी दिशा में 4 मी/से की चाल से चल रहे m द्रव्यमान के एक भारी कण से टक्कर करता है । यदि m < < m है तो टक्कर के बाद हल्के कण की चाल होगी, जबकि टक्कर पूर्ण प्रत्यास्थ हो -
View Solutionयदि संवेग 20 प्रतिशत से बढ़ता है, तो गतिज ऊर्जा किस प्रतिशत से बढ़ेगी -
View Solutionएक बंदूक जिसका द्रव्यमान M है, से एक m द्रव्यमान की गोली निकलती है, तो गोली की गतिज ऊर्जा व बंदूक की गतिज ऊर्जा का अनुपात होगा -
View Solutionm द्रव्यमान की कोई वस्तु समय `t_(1)` में विरामावस्था से `v_(1)` वेग तक एकसमान त्वरित होती है । समय के फलन के रूप में उस वस्तु को प्रदान की गई तात्क्षणिक शक्ति है
View Solutionयदि 1 किग्रा तथा 9 किग्रा वाली दो गेंदें गतिशील हैं और उनकी गतिज ऊर्जा समान है तो उनके रैखिक संवेग का अनुपात है-
View Solutionयदि द्रव्यमान - ऊर्जा समतुल्यता को सही माना जाए, तो जब जल ठंडा होकर बर्फ बनता है तब जल का द्रव्यमान -
View Solutionकिसी कण पर नियत परिमाण का कोई बल इस प्रकार कार्यरत है कि वह सदैव ही कण के वेग के लंबवत कार्य करता है तथा कण की गति किसी समतल में हो रही है । । इसका तात्पर्य यह है कि -
View Solutionझुकाव के किसी नत समतल का ऊपरी आधा भाग पूर्णत : चिकना है जबकि निचला आधा भाग खुरदुरा है । कोई वस्तु इस तल के शीर्ष से विरामावस्था से चलकर इस तल की तली पर पुनः विरामावस्था में आ जायेगी यदि निचले आधे भाग के लिए घर्षण गुणांक का मान है । -
View Solutionस्थिर अवस्था में एक 16 किग्रा द्रव्यमान का बम 4 किग्रा और 12 किग्रा द्रव्यमान के दो टुकड़ों में विस्फोटित होता है । 12 किग्रा द्रव्यमान का वेग 4 मी/से है । दूसरे द्रव्यमान की गतिज ऊर्जा है -
View Solutionएक भारहीन डोरी से एक m किग्रा द्रव्यमान को लटकाया जाता है । वह क्षैतिज बल, जो कि इस द्रव्यमान को प्रारंभिक ऊर्ध्वाधर दिशा से 45° के कोण तक विस्थापित कारण के लिए आवश्यक है, होगा -
View Solutionहाथ द्वारा बल लगाकर 0.2 किग्रा द्रव्यमान की एक गेंद को ऊर्ध्वाधर ऊपर की ओर फेंका जाता है। यदि बल लगाते समय हाथ 0.2 मीटर गति करता है तत्पश्चात गेंद 2 मीटर गति करती है तो गेंद पर हाथ द्वारा लगाया गया बल होगा -
(`g =10 "मी/से"^(2)`)
View Solution100 ग्राम द्रव्यमान के एक कण को 5 मी/से की चाल से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है । ऊपर जाने के दौरान गुरुत्व बल द्वारा किया गया कार्य होगा -
View Solution2 किग्रा द्रव्यमान का एक गुटका 4 मी/से की चाल से गतिशील है । यह बिना दबी एक स्प्रिंग से टकराता है तथा उसे तब तक दबाता है जब तक कि वह विराम में न आ जाये । यदि घर्षण बल 15 न्यूटन तथा स्प्रिंग नियतांक 10000 न्यूटन/मीटर है तो स्प्रिंग दबेगी -
View Solutionओलंपिक खेल में एक खिलाड़ी 10 सेकंड में 100 मीटर दूरी तय करता है । उसकी गतिज ऊर्जा निम्नलिखित किस प्रसार में हो सकती है -
View Solution0.5 किग्रा का एक ब्लॉक एक चिकने तल पर 2 मी/से की चाल से गति कर रहा है । यह 1 किग्रा द्रव्यमान की दूसरी वस्तु से टकराता है । इसके पश्चात वे एक वस्तु के रूप में एक साथ गति करते हैं । टक्कर के दौरान ऊर्जा क्षति है -
View Solution3.0 ग्राम द्रव्यमान के एक कण पर एक बल इस प्रकार कार्य करता है कि उसकी स्थिति समय t के अनुसार निम्न प्रकार से बदलती है-
`x=3t-4t^(2)+t^(3)` जिसमें x मीटर में तथा 1 सेकंड में है । प्रथम 4 सेकंड तक कृत कार्य होगा-
View Solutionदो समान द्रव्यमान के पिंड एक सरल रेखा के अनुदिश क्रमशः 3 मी/से और `- 5` मी/से के वेगों से गतिमान हैं । वे परस्पर प्रत्यास्थ रूप से टकराते हैं, टक्कर के पश्चात इनके वेग होंगे -
View Solutionरबर की एक गेंद को एक ग्रह पर 5 मीटर ऊँचाई से छोड़ा जाता है । टकराने के पश्चात गेंद 1.8 मीटर ऊँची उछलती है । गेंद के उछलने पर इसके वेग में किस गुणक ( factor ) की कमी होगी
View Solutionसमान रेखीय संवेग वाली दो वस्तुओं की गतिज ऊर्जाओं का अनुपात `4 : 1` है । इनके द्रव्यमानों का अनुपात होगा
View Solutionएक इंजन के लिए बल `vecF=20hati-3hatj+5hatk` न्यूटन तथा `vecv=6hati+20hatj-3hatk` वेग हैं । इंजन की शक्ति होगी -
View Solutionएक लोलक को साम्य स्थिति से `theta` कोण से विस्थापित कर दिया जाता है। यह साम्य स्थिति से किस वेग से गुजरेगा-
View Solutionएक बच्चा झूले पर झूल रहा है । झूले की पृथ्वी तल से न्यूनतम व अधिकतम ऊँचाइयाँ क्रमशः 0.75 मीटर व, 2 मीटर है । झूले का अधिकतम वेग है -
View Solutionदो स्प्रिंगों के बल नियतांक `k_(A)` और `k_(B)` इस प्रकार हैं कि `k_(B)=2k_(A)` स्प्रिंगों के चारों सिरे समान बल से खींचे जाते हैं । यदि स्प्रिंग A में संचित ऊर्जा E हो, तो स्प्रिंग B में संचित ऊर्जा होगी -
View Solutionयदि वस्तु की गतिज ऊर्जा `300 %` बढ़ा दी जाए, तो उसके संवेग में प्रतिशत वृद्धि होगी -
View Solutionद्रव्यमान m का एक कण दो बिंदुओं `x_(1)` और `x_(2)` के बीच सरल आवर्त गति में कंपन करता है । साम्य स्थिति O है । इसकी स्थितिज ऊर्जा ग्राफ होगा -
View Solution2 किग्रा और 4 किग्रा द्रव्यमान की दो गेंदें एक साथ 60 फुट ऊँची इमारत से एक साथ गिरायी जाती है । पृथ्वी की ओर 30 फुट गिरने पर उनकी गतिज ऊर्जाओं का अनुपात होगा -
View Solutionएक वस्तु पर आरोपित बल F दूरी x के साथ चित्र के अनुसार बदलता है । F न्यूटन में तथा x मीटर में है । वस्तु को x = 0 से x = 6 मीटर तक चलाने में बल द्वारा किया गया कार्य है-
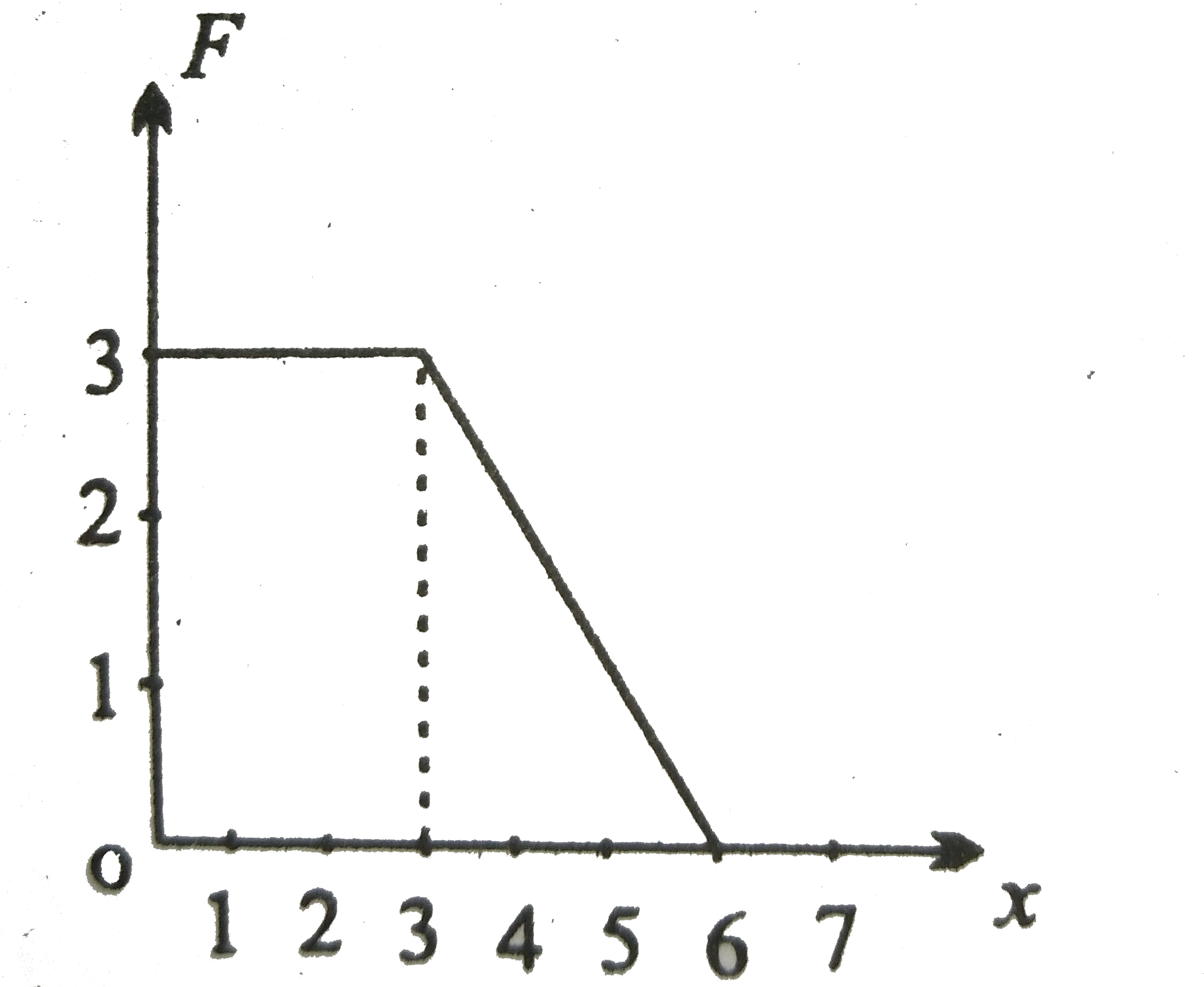
View Solution3 किग्रा द्रव्यमान के एक पिंड पर एक स्थिर बल कार्यरत है जिससे उसमें स्थान विचलन s मीटर होता है । स्थान विचलन संबंध `s =(1)/(3)t^(2)` द्वारा दिया जाता है, जहाँ t सेकंड में है । इस बल द्वारा 2 सेकंड में किया गया कार्य होगा-
View Solutionएक ऊर्ध्व स्प्रिंग मेज से खड़ा जुड़ा हुआ है । इसका बल नियतांक k है । m द्रव्यमान के एक गोले को स्प्रिंग के मुक्त सिरे के ठीक ऊपर से h ऊँचाई से गिराने पर स्प्रिंग d दूरी से पिचक जाता है इस प्रक्रम में हुआ शुद्ध कार्य होगा -
View Solutionएक टरबाइन पर 60 मीटर ऊँचाई से 15 kg per सेकंड की दर से गिरता है । ध्वनि बल के कारण `10%` ऊर्जा क्षय होती है । टरबाइन से कितनी शक्ति उत्पन्न होगी -
`(g = 10" मीटर/सेकंड"^(2))`
View Solutionइंजन रबर की नली से लगातार पानी पंप करता है । पानी नली को वेग V तथा जेट के प्रति एकांक लंबाई के द्रव्यमान m की दर से छोड़ता है । पानी को किस दर से, ऊर्जा प्राप्त होती है -
View Solution2 मीटर/सेकंड वेग से एक गेंद दुगुने द्रव्यमान की स्थिर गेंद से संघट्ट करती है । यदि प्रत्यवस्थान गुणांक 0.5 हो, तो संघट्ट के पश्चात उनके वेग ( मी/से ) होंगे
View Solutionपृथ्वी तल से प्रक्षेपित किया गया एक पिंड लौटने से पहले पृथ्वी की त्रिज्या के बराबर ऊँचाई तक पहुँचता है । गुरुत्वीय त्वरण द्वारा लगाई गई अधिकतम शक्ति होगी -
View Solution`m_(1)` और `m_(2)` द्रव्यमान के दो गोले आपस में टकराते हैं । प्रारंभ में A स्थिर तथा B वेग V से X - अक्ष के अनुदिश गतिशील हैं । टक्कर के पश्चात B का वेग `(V)/(2)` उसके प्रारंभिक वेग की लंबवत दिशा में हो जाता है । टक्कर के पश्चात द्रव्यमान A की गति की दिशा होगी -
View Solutionएक गोले को 20 मीटर ऊँचाई से प्रारंभिक वेग `v_(0)` द्वारा सीधे ऊर्ध्वाधर ऊपर की ओर फेंका जाता है । वह गोला भू तल से टकराता है । इस टक्कर में इसकी `50 %` ऊर्जा का क्षय हो जाता है । भू - तल से टकराने के बाद यह गोला उसी ऊँचाई तक उछल आता है, तो गोले का प्रारंभिक वेग है -
View Solutionएक किलोग्राम द्रव्यमान का कोई पिंड समय पर निर्भर बल `vecF=(2t hati+3t^(2)hatj)` न्यूटन के अधीन गति करता है, जहाँ `hati` और `hatj` क्रमशः X - अक्ष और Y - अक्ष के अनुदिश एकक सदिश है । समय t पर इस बल द्वारा विकसित शक्ति क्या होगी -
View Solution400 मी/से के क्षैतिज वेग से चलाती हुई 10 ग्राम की एक गोली 2 किलोग्राम द्रव्यमान के लकड़ी के एक गुटके से टकराती है । यह गुटका एक मीटर लंबी हल्की अवितान्य डोरी से लटका है । यदि गोली के टकराने के फलस्वरूप गुटके का गुरुत्व केंद्र 10 सेमी ऊर्ध्वाधर ऊपर उठ जाता है, तो गुटके से क्षैतिज दिशा में बाहर निकलने पर गोली की चाल होगी -
View Solution1 ग्राम द्रव्यमान की वर्षा के पानी की एक बूँद 1 किमी ऊँचाई से गिरती है और भू -तल से 50 मी/से की चाल से टकराती है । यदि g का मान `"10 मी/से"^(2)` स्थिर रहे तो ( i ) गुरुत्वीय बल तथा ( ii ) वायु के प्रतिरोधक बल द्वारा किया गया कार्य होगा -
View Solutionद्रव्यमान m का एक गतिशील गुटका 4m द्रव्यमान के किसी दूसरे स्थिर गुटके से संघट्ट करता है । संघट्ट के पश्चात हल्का गुटका विरामावस्था में आ जाता है । यदि हल्के गुटके का प्रारंभिक वेग v हो , तो प्रत्यानयन गुणांक का मान होगा -
View Solutionलंबाई l तथा द्रव्यमान m की एक पतली एक समान छड़ अपने एक सिरे से गुजर रहे क्षैतिज अक्ष पर स्वतन्त्र रूप से दोलन कर रही है । इसकी अधिकतम कोणीय चाल `omega` है । इसके द्रव्यमान केंद्र किस अधिकतम ऊँचाई तक उठेगा -
View Solutionकथन 1 : एक ही दिशा में गतिशील दो कण एक पूर्णतया अप्रत्यास्थ संघट्ट में अपनी संपूर्ण ऊर्जा का ह्रास नहीं करते है ।
कथन 2 : सभी प्रकार के संघट्टों के लिए संवेग के संरक्षण का नियम वैध है ।
View Solutionसमय t = 0 पर एक कण गति प्रारंभ करता है । यदि उसकी गतिज ऊर्जा समय के साथ एक समान रूप से बढ़ रही । हो , तो उस पर आरोपित बल अनुक्रमानुपाती होगा -
View Solutionदो स्प्रिंग `S_(1)` और `S_(2)` को, जिनके बल नियतांक क्रमशः `k_(1)` और `k_(2)` हैं समान बल से खींचे जाने पर स्प्रिंग `S_(2)` की तुलना में स्प्रिंग पर अधिक कार्य करना पड़ता है ।
कथन 1 : यदि स्प्रिंगें समान लंबाई तक खींची जायें तो `S_(2)` की अपेक्षा `S_(1)` पर किया गया कार्य अधिक होगा ।
कथन `2:k_(1)lt k_(2).`
View Solutionकथन 1 : द्रव्यमान m का एक बिंदु कण चाल v से चलकर द्रव्यमान M के एक स्थिर बिंदु कण से टकराता है । यदि अधिकतम ऊर्जा हानि `fxx(1)/(2)mv^(2)` हो, तो `f=(m)/(m+M)` होगा ।
कथन 2 : अधिकतम ऊर्जा की हानि तब होती है जबकि टकराने के पश्चात दोनों कण आपस में मिल जाते हैं ।
View Solutionजब एक रबर के छल्ले को `x` दूरी तक खींचा जाता है तब उस पर परिमाण `F=ax+bx^(2)` का एक प्रत्यानयन बल लगता है, जहाँ a और b नियतांक हैं । बिना खींची रबर के छल्ले को L तक खींचने में किया गया कार्य होगा -
View SolutionX - अक्ष की दिशा में चाल 2v से चलते हुए द्रव्यमान m के एक कण से Y - अक्ष की दिशा में वेग v से चलता हुआ द्रव्यमान 2m का एक कण टकराता है । यदि यह संघट्ट पूर्णतः अप्रत्यास्थ हो तो संघट्ट के दौरान ऊर्जा का क्षय होगा -
View Solutionकिसी सरल लोलक के लिए उसके विस्थापन d व गतिज ऊर्जा के बीच तथा विस्थापन व उसकी स्थितिज ऊर्जा के बीच ग्राफ खींचे गए है । निम्नांकित में से कौन - सा ग्राफ सही है-
View Solutionm द्रव्यमान का एक बिंदु कण एक खुरदरे पथ PQR ( चित्र देखिए ) पर चल रहा है । कण और पथ के बीच घर्षण गुणांक `mu` है । कण P छोड़े जाने के बाद R पर पहुँचकर रुक जाता है । पथ के भाग PQ और QR तक चलने में कण द्वारा की गई ऊर्जाएँ बराबर हैं । PQ से QR पर होने वाले दिशा बदलाव में कोई ऊर्जा व्यय नहीं होती । तब `mu` और दूरी x(QR) के मान लगभग हैं क्रमश :
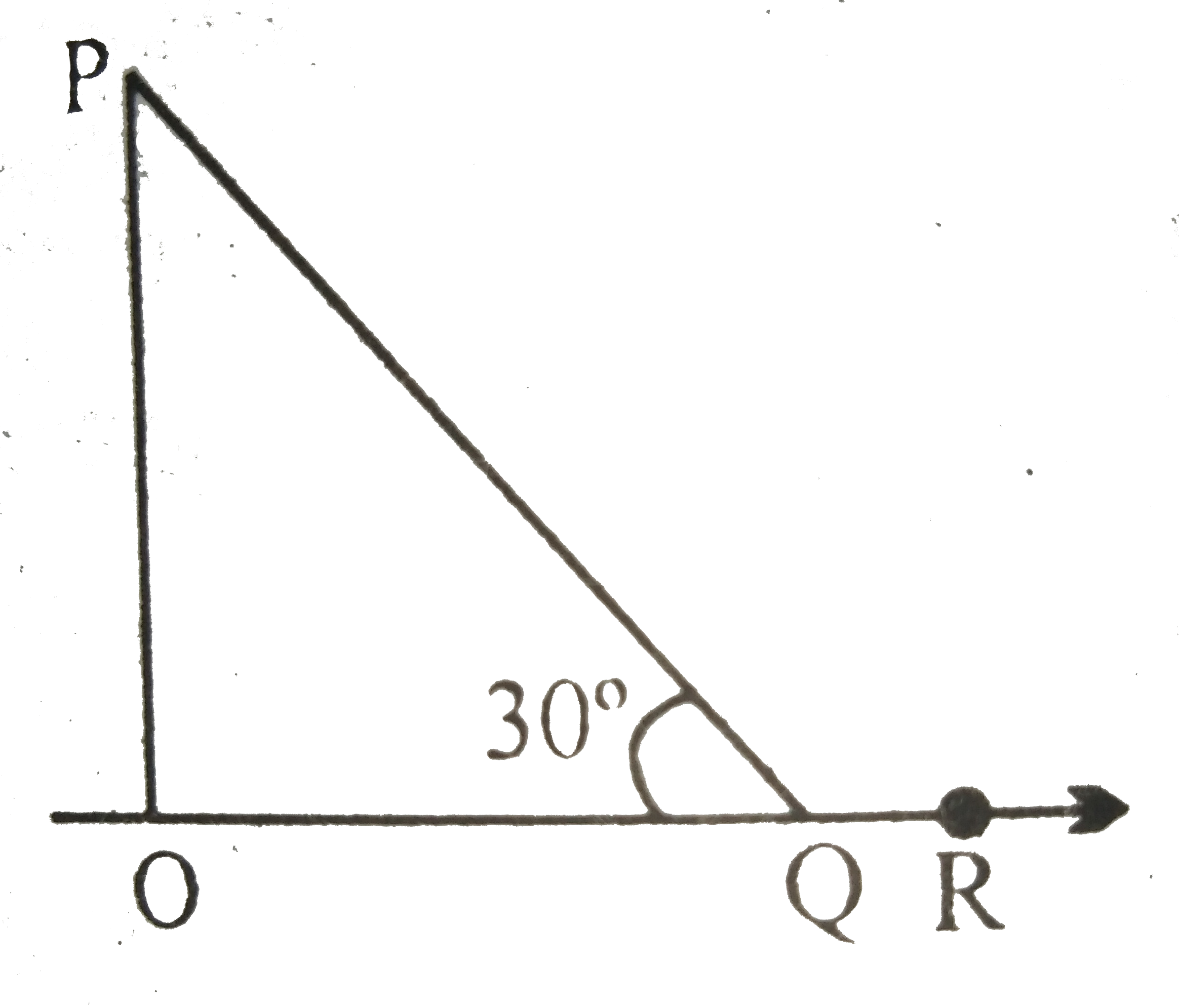
View Solutionएक भारोत्तोलक भार को पहले और फिर नीचे तक लाता है । यह माना जाता है कि सिर्फ भार को ऊपर ले जाने में कार्य होता है और नीचे लाने में स्थितिज ऊर्जा का ह्रास होता है । शरीर की वसा ऊर्जा देती है जो यांत्रिक ऊर्जा में बदलती है । मानलो कि वसा द्वारा दी गई ऊर्जा `38xx10^(7)` जूल प्रति किग्रा भार है तथा इसके केवल `20 %` भाग ही यांत्रिक ऊर्जा में परिवर्तित होता है । अब यदि भारोत्तोलक 10 किग्रा के भार को 1000 बार 1 मीटर की ऊँचाई तक ऊपर और नीचे करता हो तो इसके शरीर से वसा का क्षय होगा (` g = 9.8" मी/से"^(2)` )-
View Solutionएक किलोग्राम द्रव्यमान का एक कण समय निर्भर बल F = 6t का अनुभव करता है । यदि कण विरामावस्था से चलना प्रारंभ करता हो, तो पहले 1 सेकंड में बल द्वारा किया गया कार्य होगा -
View Solution`m=10^(-2)` किग्रा द्रव्यमान का एक पिंड एक माध्यम में गति कर रहा है और एक घर्षण बल `F=-kv^(2)` का अनुभव करता है । पिंड का प्रारंभिक वेग `v_(0)=10` मी/से है । यदि 10 सेकंड के बाद उसकी ऊर्जा `(1)/(8)mv_(0)^(2)` हो, तो k का मान होगा -
View Solutionआकर्षण प्रकृति के विभव `U=-(k)/(2r^(2))` के अंतर्गत एक कण a त्रिज्या के वृत्तीय पथ पर गतिमान है । कण की कुल ऊर्जा होगी -
View Solutionसंरेखीय संघट्ट में प्रारंभिक चाल `v_(0)` से गतिमान एक कण तुल्य द्रव्यमान के स्थिर कण से टकराता है । यदि अंतिम गतिज ऊर्जा प्रारंभिक गतिज ऊर्जा से `50 %` अधिक हो, तो संघट्ट के पश्चात दोनों कणों की आपेक्षिक गति का परिमाण होगा ।-
View Solutionएक वस्तु के R त्रिज्या वाले एक वृत्त के चारों ओर एक घेरा पूरा करने पर अभिकेंद्र बल f द्वारा किया गया कार्य होगा -
View Solutionm द्रव्यमान की एक वस्तु किसी R त्रिज्या वाले अर्द्धगोलीय प्याला के धरातल पर इसके किनारे से नीचे की तरफ सरकती है । प्याला की तली पर पहुँचाने पर वस्तु का वेग है -
View Solutionएक दिशा में चलाती हुई एक वस्तु जिसका रैखिक संवेग p है । रैखिक संवेग p समय के अनुसार बदलता है । इसके बदलने का समीकरण है `p=a+bt^(2)` जहाँ a तथा b धनात्मक नियतांक हैं । वस्तु पर लगाने वाला प्रभावी बल है -
View Solutionसरल रेखा में गति करते हुए एक पिंड का संवेग यदि `50 %` बढ़ जाता है तो उसकी गतिज ऊर्जा में प्रतिशत वृद्धि होगी -
View Solutionयदि किसी पिंड की गतिज ऊर्जा में `0.1 %` की वृद्धि होती है, तो उसके संवेग में प्रतिशत वृद्धि होगी -
View SolutionM द्रव्यमान का एक चिकना गोला u वेग से एक दूसरे स्थिर तथा m द्रव्यमान के गोले से सीधी प्रत्यास्थ टक्कर करता है । टक्कर के बाद उनके अंतिम वेग क्रमशः V तथा v हैं , v का मान है -
View Solutionकिसी स्प्रिंग का बल नियतांक K है । उसके प्रसार में `l_(1)` से `l_(2)` तक की वृद्धि करने में किया गया कार्य होगा -
View Solutionएक पिंड जिसकी संहति m तथा प्रारंभिक वेग v है , दूसरे पिंड जो कि स्थिर रखा है तथा जिसकी संहति M है, से सम्मुख टक्कर करता है । यदि टक्कर के पश्चात m संहति वाला पिंड स्थिर हो जाये और केवल M संहित वाला पिंड गति करे तो यह तभी होगा जबकि -
View Solutionअचर शक्ति देने वाली एक मशीन द्वारा एक पिंड को विराम अवस्था से सीधी रेखा में चलाते हैं । समय t में पिंड द्वारा चली दूरी अनुक्रमानुपाती होती है ।-
View SolutionV वेग से चलता हुआ m द्रव्यमान का एक गोला एक रेत के लटके बोरे में घुसकर रुक जाता है । यदि बोरे का द्रव्यमान M है और वह h ऊँचाई तक उठाया गया है तो गोले का वेग था -
View SolutionL लंबाई की एक रस्सी को F बल से खींचा जाता है । यदि जिस सिरे पर बल लगा है उससे x दूरी पर रस्सी में तनाव T है । तो T का मान है -
View Solutionयदि एक हल्के पिंड ( द्रव्यमान `M_(1)`, तथा वेग `V_(1)` ) तथा एक भारी पिंड ( द्रव्यमान `M_(2)`, तथा वेग `V_(2)` , ) दोनों की गतिज ऊर्जाएँ समान हों, तो-
View Solutionद्रव्यमान m का एक कण , वेग `vecV` से चलते हुए एक उसी द्रव्यमान के स्थिर कण से सीधी प्रत्यास्थ टक्कर करता है । टक्कर के पश्चात पहले कण का वेग होगा -
View Solution'm' द्रव्यमान की एक कार बाह्य रोधक बल 'R' के विरुद्ध त्वरण 'a' से एक सरल समतल सड़क पर गतिशील है । जब कार की गति 'V' है तब कार के इंजन की कार्य करने की दर होगी -
View Solution'm' द्रव्यमान वाला कण v वेग से गतिशील है तथा '2m' द्रव्यमान के किसी स्थिर कण से टकराकर उससे चिपक जाता है इस तंत्र का वेग होगा ।-
View Solutionचाल V से पूर्व की ओर चलते हुए द्रव्यमान का एक कण समान द्रव्यमान तथा समान चाल V से उत्तर की ओर चलते हुए एक - दूसरे कण से टकरा जाता है तथा दोनों कण संलयित हो जाते हैं । इस 2m द्रव्यमान के नये कण की चाल होगी-
View Solutionतोप से एक गोला क्षैतिज से कोण `theta` बनाते हुए वेग v मी./से. से छोड़ा जाता है । अपने पथ के उच्चतम बिंदु पर उसमें विस्फोट होकर वह समान द्रव्यमान के दो टुकड़ों में फट जाता है । इनमें से एक टुकड़ा अपना पथ दोहराते हुए तोप पर वापस जा पहुँचता है । विस्फोट के तुरंत बाद दूसरे टुकड़े की चाल मी./से. में होगी -
View Solutionm द्रव्यमान तथा vवेग से गतिमान एक गोली M द्रव्यमान के स्थिर गुटके से टकराकर उसमें धँस जाती है । संयुक्त गुटके की गतिज ऊर्जा होगी -
View Solutionk बल नियतांक वाली एक स्प्रिंग का एक - चौथाई भाग काट कर अलग कर दिया जाता है । शेष स्प्रिंग का बल नियतांक होगा -
View Solutionदो स्प्रिंगों के बल नियतांक क्रमशः `k_(1)` तथा `k_(2)` हैं । इन्हें इतना खींचा जाता है कि दोनों की स्थितिज ऊर्जायें समान हो जायें । इन पर लगाए गये `f_(1)` बलों `f_(2)` तथा का अनुपात होगा-
View Solutionm द्रव्यमान की एक गेंद वेग से चलकर 2v वेग से सामने से आती हुई समान द्रव्यमान की दूसरी गेंद से सम्मुख प्रत्यास्थ टक्कर करती है । वेग की दिशा को धनात्मक मानते हुए टक्कर के बाद गेंदों के वेग होंगे -
View Solutionकेंद्रीय बल के क्षेत्र में क्या नहीं बदलता है -
View Solutionएक बंदूक जिसका द्रव्यमान M है , से एक m द्रव्यमान की गोली निकलती है, तो गोली की गतिज ऊर्जा व बंदूक की गतिज ऊर्जा का अनुपात होगा-
View Solutionm द्रव्यमान की कोई वस्तु समय `t_(1)` में विरामावस्था से `v_(1)` वेग तक एकसमान त्वरित होती है । समय t के फलन के रूप में उस वस्तु को प्रदान की गई तात्क्षणिक शक्ति है -
View Solutionचित्र में दर्शाये अनुसार घर्षण रहित पथ ABCD का अंतिम भाग वृत्ताकार है , जिसकी त्रिज्या R है । यदि बिंदु A की ऊँचाई h = 5 सेमी हो तो वृत्त की अधिकतम त्रिज्या r क्या होगी जिससे बिंदु a से छोड़ा गया एक पिंड फिसलकर गोलाकार पथ का चक्कर लगा ले -
View Solutionदो कण A तथा B क्रमशः स्थिर वेग `vecv_(1)` और `vecv_(2)` से गति कर रहे हैं । प्रारंभिक क्षण में उनके स्थिति सदिश क्रमशः `vecr_(1)` और `vecr_(2)` में हैं, तो कणों के संघट्ट होने के लिए प्रतिबंध हैं -
View Solutionकिसी घर्षण रहित पृष्ठ पर v चाल से चलता हुआ M द्रव्यमान का एक ब्लॉक उसी द्रव्यमान M के विरामावस्था में स्थित एक अन्य ब्लॉक `(v)/(3)` से प्रत्यास्थ संघट्ट करता है । टक्कर के पश्चात पहला ब्लॉक चाल से अपनी प्रारंभिक गति की दिशा से `theta` कोण से चलने लगता है, तो टक्कर के पश्चात दूसरे ब्लॉक की चाल होगी -
View Solution
बहुविकल्पीय प्रश्न questions and complete solutions for chapter कार्य, ऊर्जा और शक्ति of NAVBODH PHYSICS (HINDI) of Class 11
All Exercises from NAVBODH PARIKSHA SAAR Class 11 PHYSICS कार्य, ऊर्जा और शक्ति
- NCERT पाठ्यपुस्तक के प्रश्नोत्तर
- अभ्यासार्थ प्रश्न (अति लघु उत्तरीय प्रश्न/एक शब्द/एक वाक्य )
- अभ्यासार्थ प्रश्न (उचित संबंध जोड़िए - )
- अभ्यासार्थ प्रश्न (दीर्घ उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (मूल्य आधारित प्रश्न )
- अभ्यासार्थ प्रश्न (रिक्त स्थानों की पूर्ति कीजिए - )
- अभ्यासार्थ प्रश्न (लघु उत्तरीय प्रश्न )
- अभ्यासार्थ प्रश्न (वस्तुनिष्ठ प्रश्न ) (बहुविकल्पीय प्रश्न )
- अभ्यासार्थ प्रश्न (सत्य/असत्य लिखिए - )
- आंकिक उदाहरण
- आंकिक उदाहरण प्लस
- आंकिक प्रश्न
- उदाहरण
- तथ्यात्मक प्रश्न
- बहुविकल्पीय प्रश्न
- बोधात्मक प्रश्न
- बोधात्मक प्रश्न प्लस