Complete Solutions to उदाहरण of chapter सम्मिश्र संख्याएँ और दिघात समीकरण of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | सम्मिश्र संख्याएँ और दिघात समीकरण |
| NCERT EXEMPLAR HINDI | उदाहरण |
| Number Of Questions | 33 |
| Academic Year | 2023-24 |
मान ज्ञात कीजिए : `(1+i)^(6)+(1-i)^(3)`
View Solutionयदि `(x+iy)^(1/3)=a+ib`, जहाँ `y,a,b epsilon R` तो दर्शाइए कि `(x)/(a)-(y)/(b)=-2(a^(2)+b^(2))`
View Solutionसमीकरण `z^(2)=bar(z)` को हल कीजिए, जहाँ `z=x+iy` हैं।
View Solutionयदि `(2z+1)/(iz+1)` का काल्पनिक भाग -2 हैं, तो दर्शाइए कि z को आर्गड तल में निरूपित करने वाले बिंदु का बिंदु पथ एक सरल रेखा हैं।
View Solutionयदि `|z^(2)-1|=|z|^(2)+1` हैं, तो दर्शाइए कि z काल्पनिक अक्ष पर स्थित हैं।
View Solutionमान लीजिए कि `z_(1)` और `z_(2)` दो सम्मिश्र संख्याएँ इस प्रकार हैं कि `bar(z_(1))+ibar(z)_(2)=0` हैं तथा `"arg"(z_(1)z_(2))=pi` , तब `"arg"(z_(1))` ज्ञात कीजिए।
View Solutionमान लीजिए कि `z_(1)` और `z_(2)` दो सम्मिश्र संख्याएँ इस प्रकार हैं कि `|z_(1)+x_(2)|=|z_(1)|+z_(2)|` तब दर्शाइए कि `"arg"(z_(1))-"arg"(z_(2))=0`
View Solutionयदि `z_(1),z_(2),z_(3)` ऐसी सम्मिश्र संख्याएँ हैं कि `|z_(1)|=|z_(2)|=|z_(3)|=|(1)/(z_(1))+(1)/(z_(2))+(1)/(z_(3))|=1` तो `|z_(1)+z_(2)+z_(3)|` का मान ज्ञात कीजिए।
View Solutionयदि एक सम्मिश्र संख्या z त्रिज्या `3` इकाई और केंद्र `(-4,0)` वाले एक वृत्त के अभ्यंतर या उसकी परिसीमा पर स्थित हैं, तो `|z+1|` के अधिकतम और न्यूनतम मान ज्ञात कीजिए।
View Solutionवे बिंदु निर्धारित कीजिए, जिनके लिए `3lt|z|lt4`
View Solution`2x^(4)+5x^(3)+7x^(2)-x+41` का मान ज्ञात कीजिए, जब `x=-2-sqrt(3)i`
View SolutionP का वह मान ज्ञात कीजिए जिसके लिए समीकरण `x^(2)-Px+8=0` के मूलों का अंतर `2` हो।
View Solutiona का वह मान ज्ञात कीजिए जिसके लिए समीकरण `x^(2)-(a-2)x-(a+1)=0` के मूलों के वर्गों का योग न्यूनतम है।
View Solutionयदि सम्मिश्र संख्याओं `z(1)` और `z_(2)` के लिए, `|1-(z(1))z_(2)|^(2)-|z_(1)-z_(2)|^(2)=k(1-|z_(1)|^(2))(1-|z_(2)|^(2))` तो k का मान ज्ञात कीजिए।
View Solutionयदि `z_(1)` और `z_(2)` दोनों `z+bar(z)=2|z-1|` जहाँ `"arg"(z_(1)-z_(2))=(pi)/(4)` को संतुष्ट करते है, तो `Im(z_(1)+z_(2))` ज्ञात कीजिए।
View Solutionनिम्नलिखित में रिक्त स्थानों की पूर्ति कीजिए :
(i) किन्हीं दो सम्मिश्र संख्याओं `z_(1),z_(2)` और किन्हीं वास्तविक संख्याओं a,b, के लिए, `|az_(1)-bz_(2)|^(2)+|bz_(1)+az_(2)|^(2)=.....`
(ii) `sqrt(-25)xxsqrt(-9)` का मान ….हैं।
(iii) संख्या `((1-i)^(3))/(1-i^(3))....` के बराबर हैं
(iv) श्रेणी `i+i^(2)+i^(3)+....` का `1000` पदों तक का योग ...... हैं।
(v) `1+i` का गुणनात्मक प्रतिलोम ..... हैं।
(vi) यदि `z_(1)` और `z_(2)` ऐसी सम्मिश्र संख्याएँ हैं कि `z_(1)+z_(2)` एक वास्तविक संख्या हैं, तो `z_(2)=....`
(vii) `"arg"(z)+"arg"bar(z)(bar(z) ne 0)....` हैं।
(viii) यदि `|z+4|le 3` तो `|z+1|` के अधिकतम और न्यूनतम मान .... एवं .... हैं।
(ix) यदि `|(z-2)/(z+2)|=(pi)/(6)` हैं, तो z का बिंदु पथ .... हैं।
(x) यदि `|z|=4` और `"arg"(z)=(5pi)/(6)`, तो z=.........
View Solutionबताइए कि निम्नलिखित में से कौन सा कथन सत्य है और कौन सा असत्य है।
(i) एक शून्येतर सम्मिश्र संख्या को i से गुणा करने पर, वह उसे वामावर्त दिशा में एक समकोण पर घुमा देता है।
(ii) सम्मिश्र संख्या `cos theta +i sin theta, theta` के किसी मान के लिए शून्य हो सकती है।
(iii) यदि कोई सम्मिश्र संख्या अपने संयुग्मी के साथ संपाती है, तो वह संख्या अवश्य ही काल्पनिक अक्ष पर स्थित होना चाहिए।
(iv) सम्मिश्र संख्याएं `z=(1+isqrt(3))(1+i)(cos theta+i sin theta)` का कोणांक `(7pi)/(12)+theta` है।
(v) सम्मिश्र संख्या z, जिसके लिए `|z+1|lt|z-1|` है, को निरूपित करने वाले बिंदु एक वृत्त के अभ्यंतर में स्थित होते है।
(vi) यदि तीन सम्मिश्र संख्याएँ `z_(1),z_(2)` और `z_(3)` एक समांतर श्रेणी (A.P) में हैं तो वे सम्मिश्र तल में एक वृत्त पर स्थित होते हैं।
(vii) यदि n एक धनात्मक पूर्णांक हैं, तो `i^(n)+(i)^(n+1)+(i)^(n+2)+(i)^(n+3)` का मान शून्य हैं।
View Solutionनिम्नलिखित स्तंभ A को स्तंभ B से मिलाये
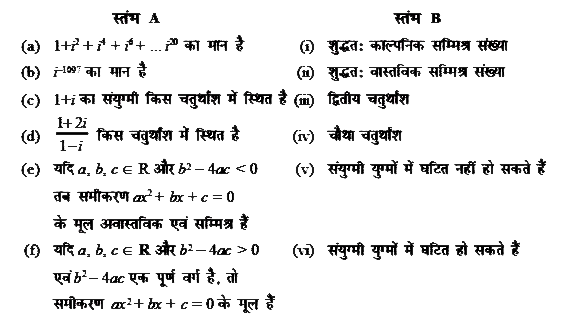
View Solution`(i^(4n+1)-i^(4n-1))/(2)` का क्या मान है ?
View Solutionवह कौन-सा न्यूनतम धनात्मक पूर्णांक n है, जिसके लिए `(1+i)^(2n)=(1-i)^(2n)?`
View Solution`3+sqrt(7)i` का व्युत्क्रम क्या है ?
View Solutionयदि `z_(1)=sqrt(3)+isqrt(3)` और `z_(2)=sqrt(3)+i` तो ज्ञात कीजिए कि `((z_(1))/(z_(2)))` किस चतुर्थांश में स्थित है।
View Solution`(sqrt(5+12i)+sqrt(5-12i))/(sqrt(5+12i)-sqrt(5-12i))` का संयुग्मी क्या है ?
View Solution`1-i` के कोणांक का मुख्य मान क्या है ?
View Solutionसम्मिश्र संख्या `(i^(25))^(3)` का ध्रुवीय रूप क्या है ?
View Solutionz का बिंदु पथ क्या होगा, यदि `z-2-3i` का कोणांक `(pi)/(4)` है ?
View Solutionयदि `1-i` समीकरण `x^(2)+ax+b=0` का एक मूल है, जहाँ `a, b epsilon R`, तब a और b के मान ज्ञात कीजिए।
View Solution`1+i^(2)+i^(4)+i^(6)+…+i^(2n)` है :
View Solutionयदि सम्मिश्र संख्या `z=x+iy` प्रतिबंध `|z+1|=1` को संतुष्ट करती है, तो z स्थित है :
View Solutionसम्मिश्र संख्याओं `z,-iz` और `z+iz` द्वारा सम्मिश्र तल में बनाये गये त्रिभुज का क्षेत्रफल है।
View Solutionसमीकरण `|z+1-i|=|z-1+i|` निरूपित करता है एक
View Solutionसमीकरण `z^(2)+|z|^(2)=0, z ne 0` के हलों की संख्या है
View Solution`sin.(pi)/(5)+i(1-cos.(pi)/(5))` का कोणांक है
View Solution
उदाहरण questions and complete solutions for chapter सम्मिश्र संख्याएँ और दिघात समीकरण of NCERT MATHS (HINDI) of Class 11