Complete Solutions to उदाहरण of chapter शंकु परिच्छेद of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | शंकु परिच्छेद |
| NCERT EXEMPLAR HINDI | उदाहरण |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
वृत्त `x^(2)+y^(2)-2x+4y=8` की त्रिज्या एवं केंद्र ज्ञात कीजिए।
View Solutionयदि `x^(2)=-8y` किसी परवलय का समीकरण है तो नाभि के निर्देशांक, नियता का समीकरण और नाभिलंब जीवा की लम्बाई ज्ञात कीजिए।
View Solutionयदि एक दीर्घवृत्त का समीकरण `9x^(2)+25y^(2)=225`, है तो दीर्घ अक्ष, लघु अक्ष, उत्केंद्रता, नाभियां एवं शीर्ष ज्ञात कीजिए।
View Solutionएक ऐसे दीर्घवृत्त का समीकरण ज्ञात कीजिए जिसकी नाभियां `(+-5,0)` पर है ओर एक नियता का समीकरण `x=36/5` है।
View Solutionअतिपरवलय `9x^(2)-16y^(2)=144` के लिए शीर्ष, नाभियां एवं उत्केंद्रता ज्ञात कीजिए।
View Solutionएक ऐसे अतिपरवलय का समीकरण ज्ञात कीजिए जिसके शीर्ष `(0,+-6)` पर हैं एवं `e=5/3`
View Solutionबिंदुओं `(20,3),(19,8)` और `(2,-9)` से गुजरने वाले वृत्त का समीकरण ज्ञात कीजिए। वृत्त का केंद्र एवं त्रिज्या भी ज्ञात कीजिए।
View Solutionपरवलय `y^(2)=4ax` के अंतर्गत एक समबाहु त्रिभुज इस प्रकार बनाया जाता है कि त्रिभुज का एक शीर्ष, परवलय के शीर्ष पर हैं त्रिभुज की भुजा की लम्बाई ज्ञात कीजिए।
View Solutionएक ऐसे दीर्घवृत्त का समीकरण ज्ञात कीजिए जो बिंदु `(-3,1)` से जाता है एवं उसकी उत्केंद्रता `sqrt(2/5)` है। दीर्घ अक्ष x- अक्ष पर है और केंद्र मूल बिंदु पर है।
View Solutionएक ऐसे अतिपरवलय का समीकरण ज्ञात कीजिए जिसके शीर्ष `(+-6,0)` पर है और किसी एक नियता का समीकरण `x=4` है।
View Solutionमूल बिंदु से 1 इकाई की दूरी पर प्रत्येक निर्देशांक अक्ष का स्पर्श करने वाले वृत्त का प्रथम चतुर्थांश में समीकरण है
View Solutionरेखाओं `3x+y=14` एवं `2x+5y=18` के प्रतिच्छेद बिंदु से जाने वाले उस वृत्त का समीकरण जिसका केंद्र (1,-2) है।
View Solutionपरवलय `x^(2)+12y` के शीर्ष को नाभिलंब जीवा के अंत्य बिंदुओं से मिलाने पर बने त्रिभुज का क्षेत्रफल है।
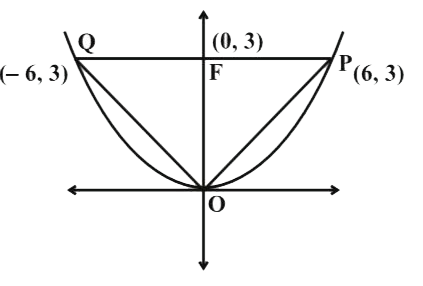
View Solutionपरवलय `y^(2)=6x` के शीर्ष को इसके ऐसे बिंदुओं, जिनका भुज (x- निर्देशांक)24 है से मिलाने पर, प्राप्त रेखाओं के समीकरण है
View Solutionएक दीर्घ वृत्त का केंद्र मूल बिंदु है एवं दीर्घ अक्ष, x- अक्ष पर है यह बिंदुओं (-3,1) एवं (2,-2) से जाता है । उस दीर्घवृत्त का समीकरण है
View Solutionएक अतिपरवलय का केंद्र मूल बिंदु पर है एवं इसके अनुप्रस्थ अक्ष जो x- अक्ष के अनुदिश है की लम्बाई 7 है। यह अतिपरवलय बिंदु (5,-2) से जाता है। अतिपरवलय का समीकरण है:
View Solutionएक वृत्त पर किसी भी बिंदु के निर्देशांक `(2+4 cos theta, -1+4sin theta)` है जहां `theta` प्राचल हैं उस वृत्त का समीकरण `(x-2)^(2)+(y+1)^(2)=16` है
View Solutionदी हुई लम्बाई की एक छड़ इस प्रकार घूमती है कि इसके अंतिम छोर, परस्पर लंब दो निश्चित सरल रेखाओं पर ही रहते हैं। छड़ पर लिया हुआ कोई भी बिंदु दीर्घवृत्त को दर्शाता है।
View Solutionबिंदु (2,2) पर केंद्र एवं बिंदु (4,5) से जाने वाले वृत्त का समीकरण__________ है।
View Solutionएक वृत्त की त्रिज्या 3 इकाई है और इसका केंद्र रेखा `y=x-1` पर स्थित है। यदि यह वृत्त बिंदु (7,3) से जाता है तो इसका समीकरण----------------- है।
View Solutionएक दीर्घवृत्त का अक्ष x- अक्ष के अनुदिश है और इसका केंद्र मूल बिंदु पर है। इसके नाभिलंब जीवा की लम्बाई 10 इकाई है। यदि नाभियों के बीच की दूरी –लघु अक्ष की लम्बाई, तो दीर्घवृत्त का समीकरण-------------- है।
View Solutionएक परवलय की नाभि, बिंदु (2,3) है एवं रेखा `x-4y+3=0` उसकी नियता है उस परवलय का समीकरण---------- है।
View Solutionबिंदुओं (3,0) एवं `(3sqrt(2),2)` से जाने वाले अतिपरवलय `(x^(2))/(a^(2))-(y^(2))/(b^(2))=1` की उत्केंद्रता---------------- है।
View Solution
उदाहरण questions and complete solutions for chapter शंकु परिच्छेद of NCERT MATHS (HINDI) of Class 11