Complete Solutions to बहुविकल्प प्रश्न पिटारा - प्रक्षेप्य गति of chapter समतल में गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | समतल में गति |
| NCERT FINGERTIPS HINDI | बहुविकल्प प्रश्न पिटारा - प्रक्षेप्य गति |
| Number Of Questions | 29 |
| Academic Year | 2023-24 |
एक क्रिकेट खिलाड़ी गेंद को अधिकतम `100` m की क्षैतिज दूरी तक फेंक सकता है। वही खिलाड़ी उसी गेंद को समान चाल से मैदान से कितनी ऊँचाई तक फेंक सकता है ?
View Solutionकिसी कण को हवा में उस तल से `beta` कोण पर प्रक्षेपित किया जाता है जो स्वय ही क्षैतिज से `alpha` कोण पर झुका हुआ है। तब L दूरी बराबर होती है -

View Solutionएक पर्वतारोही किसी पहाड़ी पर मैदान से `490` m की ऊँचाई पर खड़ा होकर एक पत्थर को `15` m/s की चाल से क्षैतिज दिशा में फेंकता है। पत्थर को मैदान पर पहुँचने में लगने वाला समय है -
View Solutionप्रश्न क्रमांक `47` में पत्थर, के मैदान से टकराने की चाल है -
View Solutionकिसी फुलबॉल को हवा में ऊर्ध्वाधर दिशा में u वेग से फेंका जाता है। फुटबॉल का उच्चतम बिन्दु पर वेग होता है -
View Solutionक्षैतिज रूप से उड़ रहे एक वायुयान से एक गोले (Bomb) को गिराया जाता है। गोले के मार्ग का आकार होगा
View Solutionकिसी प्रक्षेप्य गति के प्रकरण में, उच्चतम बिन्दु पर वेग तथा त्वरण के बीच का कोण क्या होता है ?
View Solutionएक क्रिकेट खिलाड़ी गेंद को `100` m की अधिकतम क्षैतिज दूरी से फेंक सकता है। वही खिलाड़ी उसी गेंद को मैदान से कितनी ऊँचाई तक फेंक सकेगा।
View Solutionक्रिकेट की एक गेंद को `30^(@)` के कोण से क्षैतिज से `u=30` m/s, ऊपर की ओर फेंका जाता है। गेंद को वापस समान स्तर पर आने में लगा समय होगा ( `g= 10m//s^(2)` लेने पर )
View Solutionप्रश्न संख्या `53` में, फेंकने वाले से उस बिन्दु की दूरी जहाँ पर गेंद समान स्तर पर वापस होती है, है -
View Solutionप्रक्षेप्य गति के बारे में निम्न में से कौन- सा सही है ?
View Solutionएक `360` km/h की चाल से क्षैतिज में उड़ने वाला वायुयान `490` m की ऊँचाई से मैदान पर गोला (Bomb) गिराता है। यदि `g=9.8m//s^(2)` तब यह मैदान पर कितनी दूर पर टकराएगा ?
View Solutionकिसी प्रक्षेप्य की गति के समीकरण `x=36` t m तथा `2y=96t-9.8t^(2)` m द्वारा दिये गये है। तो प्रक्षेपण का कोण है -
View Solutionगैलीलियो लिखते हैं कि `(45^(@)+theta)` तथा `(45^(@)-theta)` कोणों पर प्रक्षेपित प्रक्षेप्य के क्षैतिज परासों का अनुपात होगा (यदि `thetage45^(@)`)
View Solutionकिसी हॉल की छत `40` m ऊँची हैं। अधिकतम क्षैतिज दूरी के लिए, वह कोण कितना होगा जिस पर `56` m/s की चाल से फेंकी गई कोई गेंद छत से टकराए बिना गुजर जाये ?
View Solutionप्रश्न संख्या `59` में अधिकतम क्षैतिज दूरी होगी -
View Solutionदो प्रक्षेप्यों के समान बिन्दु से समान चाल से क्रमश: `60^(@)` व `30^(@)` के प्रक्षेप्य कोणों से फेंका जाता हैं। निम्न में से कौन-सा सही हैं ?
View Solutionदो गेंदें समान चाल से क्षैतिज से `theta` और `(90^(@)-theta)` के कोणों पर फेंकी जाती है। उनकी अधिकतम ऊर्ध्वाधर ऊँचाइयों का अनुपात है -
View Solutionयदि R एवं H प्रक्षेप्य की क्षैतिज परास एवं अधिकतम ऊँचाई है, तो क्षैतिज से प्रक्षेपण का कोण होगा -
View Solutionप्रक्षेप्य के उडडयन काल, `T_(f)` एवं अधिकतम ऊँचाई तक पहुँचने का काल, `t_(m)` के बीच सम्बन्ध है -
View Solutionप्रक्षेप्य की गति के संबंध में विचार करते समय जब वायु के प्रतिरोध को ध्यान में रखा जाता है तब प्रक्षेप्य का निम्न में से कौन-सा गुण, बढ़ोत्तरी को दर्शाता है ?
View Solutionदो कणो को समान ऊर्ध्वाधर तल, समान बिन्दु से, दोनों ही को विभिन्न गतियों तथा क्षैतिज से भिन्न कोणों पर एक साथ प्रक्षेपित किया जाता है। दूसरे कण के द्वारा देखा गया पहले कण का पथ होगा -
View Solutionकिसी प्रक्षेप्य की गति का समीकरण `y=ax-bx^(2)` है, जहाँ a एवं b गति के नियतांक है। स्तंभ-I की राशियों को स्तंभ-II के संबंधो से मिलान कीजिए।
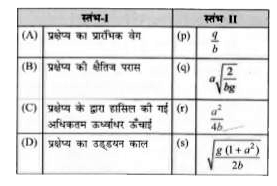
View Solutionदो कणो को क्षैतिज में क्रमश: `theta_(1)` एवं `theta_(2)` (दोनों ही तीक्ष्ण ) के कोण पर u चाल से हवा में प्रक्षेपित किया जाता है। यदि पहले कण के द्वारा हासिल की गई ऊँचाई दूसरे की तुलना में अधिक है, तो निम्न में से कौन-सा सही है ?
जहाँ `T_(1)` व `T_(2)` उडडयन काल है।
View Solutionयदि किसी पिण्ड को क्षैतिज में `theta` कोण से प्रक्षेपित किया जाता है, तो
View Solutionएक गेंद को किसी मीनार के शीर्ष से क्षैतिज से `30^(@)` के कोण पर `10` m/s के आरंभिक वेग से फेंका जाता है। यदि यह मैदान पर मीनार के पीछे से `17.3` की दूरी से टकराती है, तो मीनार की ऊँचाई है -
View Solutionकिसी प्रक्षेप्य की इसकी अधिकतम ऊँचाई पर चाल उसकी आरंभिक चाल की `(sqrt(3))/(2)` गुनी है। यदि प्रक्षेप्य की परास इसके द्वारा तय की गई ऊँचाई की P गुनी है, तो P बराबर है -
View Solutionचार पिण्डों A, B, C एवं D को समान वेगों से क्षैतिज के साथ क्रमश: `15^(@), 30^(@), 45^(@)`, एवं `60^(@)` के कोणों से प्रक्षेपित किया जाता है, तो लघुत्तम परास (Shortest range) वाला पिण्ड होगा -
View Solutionकोई खिलाड़ी किसी गेंद को `20` m/s की चाल से इस प्रकार से मारता है कि वह अधिकतम क्षैतिज परास को पा सके। मारने की दिशा में `24` m दूर एक अन्य खिलाड़ी प्रहार (Hit) के क्षण से ही समान दिशा में दौड़ना आरंभ करता है। यदि उसे गेंद को मैदान पर पहुँचने से ठीक पहले पकड़ना है, तब उसे इस वेग से दौड़ना चाहिए - यहाँ `g=10m//s^(2))`
View Solution
बहुविकल्प प्रश्न पिटारा - प्रक्षेप्य गति questions and complete solutions for chapter समतल में गति of MTG PHYSICS (HINDI) of Class 11
All Exercises from NCERT FINGERTIPS HINDI Class 11 PHYSICS समतल में गति
- अभिकथन एवं तर्क प्रारूप प्रश्न
- एन. सी. ई. आर. टी. प्रश्न प्रदर्शिका
- बहुविकल्प प्रश्न पिटारा - अदिश एवं सदिश
- बहुविकल्प प्रश्न पिटारा - एकसमान वृत्तीय गति
- बहुविकल्प प्रश्न पिटारा - किसी समतल में गति
- बहुविकल्प प्रश्न पिटारा - द्विविमीय गति में आपेक्षिक वेग
- बहुविकल्प प्रश्न पिटारा - नियत त्वरण से किसी समतल में गति
- बहुविकल्प प्रश्न पिटारा - प्रक्षेप्य गति
- बहुविकल्प प्रश्न पिटारा - विविध प्रश्न
- बहुविकल्प प्रश्न पिटारा - सदिशों का योग - विश्लेषणात्मक विधि
- बहुविकल्प प्रश्न पिटारा - सदिशों का योग एवं घटाव : ग्राफीय विधि
- बहुविकल्प प्रश्न पिटारा - सदिशों का वियोजन