Complete Solutions to बहुविकल्प प्रश्न पिटारा of chapter कणों के निकाय घूर्णी गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | कणों के निकाय घूर्णी गति |
| NCERT FINGERTIPS HINDI | बहुविकल्प प्रश्न पिटारा |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
किसी घूमते हुए लटू (Top) का अक्ष, फर्श पर शंकु के रूप में अपने संपर्क बिंदु (Point of contact) में से ऊर्ध्वाधर (Vertical) के चारों ओर घूमता है। ऊर्ध्वाधर के चारों ओर लटू के अक्ष की यह गति कहलाती है-
View Solution1 किग्रा, `(3/2)` किग्रा, एवं 2 किग्रा द्रव्यमानों के तीन कण a भुजा वाले एक समबाहु त्रिभुज के शीर्षों पर रखे गये हैं। द्रव्यमान केन्द्र के X, Y निर्देशांक होंगे-
View Solution1 किग्रा, 2 किग्रा तथा 3 किग्रा द्रव्यमानों के तीन कणों का द्रव्यमान केन्द्र, बिन्दु (1, 2, 3) पर स्थित है तथा 3 किग्रा एवं 2 किग्रा के कणों के अन्य निकाय का द्रव्यमान केन्द्र, बिन्दु (-1, 3, -2) पर स्थित है। 5 किग्रा द्रव्यमान के एक कण को हमें कहा रखना चाहिए ताकि सम्पूर्ण निकाय का द्रव्यमान केन्द्र, पहले निकाय के द्रव्यमान केन्द्र पर स्थित हो?
View Solutionएकसमान द्रव्यमान घनत्व के किसी घन के द्रव्यमान केन्द्र की स्थिति क्या होगी?
View Solutionm एवं 2m द्रव्यमानों वाले दो कणों का अपघटित द्रव्यमान (Reduced mass) होगा-
View Solution3 किग्रा द्रव्यमान के L-आकार के एकसमान पटल के द्रव्यमान केन्द्र के x, y निर्देशांक क्या हैं?
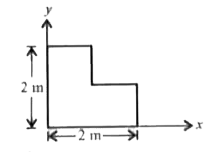
View Solution`m_(1)` व `m_(2)` द्रव्यमानों के दो कणों के किसी निकाय का द्रव्यमान केन्द्र, `m_(1)` से `d_(1)` दूरी पर तथा `m_(2)` से `d_(2)` दूरी पर इस प्रकार से है कि
View Solutionकिसी पिण्ड का द्रव्यमान केन्द्र
View Solution1 किग्रा तथा 3 किग्रा द्रव्यमान के दो कणों के स्थिति सदिश (Position vectors) क्रमशः `2hati +3hatj+4hatk` तथा `-2hati+3hatj-4hatk` हैं। द्रव्यमान केन्द्र का स्थिति सदिश क्या है?
View Solutionयदि गुरुत्व के प्रभाव में किसी परवलयाकार मार्ग में गति करते हुए किसी विस्फोटक पदार्थ का विस्फोट हवा के मध्य होता है, तब उसके टुकड़ों का द्रव्यमान केन्द्र गति करेगा-
View Solutionदो द्रव्यमानों, `m_(1) = 1` किग्रा तथा `m_(2) = 2` किग्रा को एक हल्की अवितान्य (Inextensible) डोरी के द्वारा भारहीन पुली के माध्यम से चित्रानुसार निलंबित किया गया है। यह मानते हुए कि दोनों ही द्रव्यमान विरामावस्था से शुरू होते हैं, दो सेकण्ड में द्रव्यमान केन्द्र के द्वारा तय की गई दूरी होगी-
(g= `10 m//s^2` लीजिए)।
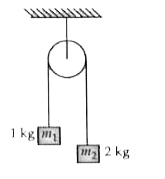
View Solutionबराबर द्रव्यमानों के दो कणों के वेग `vecv_(1)=2hati ` मी / सेकण्ड"तथा `vecv_(2) = 2hatj` मी / "सेकण्ड" हैं। पहले कण का त्वरण `veca_(1)= (3hati +3hatj) `मी/ सेकण्ड है जबकि अन्य कण का त्वरण शून्य है। दोनों कणों का द्रव्यमान केन्द्र किस मार्ग (Path) में गति करता है?
View Solutionएक चिकने क्षैतिज तल पर v चाल से गति कर रही एक लम्बी ट्रॉली के एक सिरे पर एक बच्चा खड़ा है। यदि बच्चा u चाल से ट्रॉली के दूसरे सिरे की ओर दौड़ना प्रारंभ करता है, तो इस निकाय (ट्रॉली + बच्चा) के द्रव्यमान केन्द्र की चाल क्या होगी?
View Solutionकिसी कण के रेखीय वेग `vecv` तथा कोणीय वेग `vecomega` के मध्य निम्न में से कौन-सा सम्बन्ध सही है?
View Solutionकोणीय वेग सदिश की दिशा किसके अनुदिश होती है?
View Solutionनिम्न में से कौन-सा कथन सही है?
View Solutionकोई पिण्ड कोणीय वेग `vecomega= (3hati-4hatj+hatk)` से घूम रहा है। स्थिति सदिश `vecr= (5hati-6hatj +6hatk)` वाले किसी बिन्दु का रेखीय वेग है-
View Solutionकोणीय चाल `omega_(0)` से अपने अक्ष के परितः घूर्णन कर रही किसी चकती को धीरे से (कोई स्थानान्तरण धक्का दिए बिना) किसी पूरी तरह से घर्षण रहित मेज पर रखा जाता है। चकती की त्रिज्या R है।
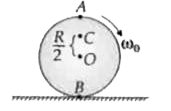
चित्र में दिखाए अनुसार, माना `v_(A), v_(B)` एवं `v_(C)`, चकती पर बिन्दुओं A, B, व C के रेखीय वेगों के परिमाण हैं। तब
View Solutionकिसी ऐसे कण के कोणीय संवेग का z घटक क्या होगा जिसका x, y एव z : घटकों के साथ स्थिति सदिश `vecr` हो तथा `P_(x), P_(y)` एवं `P_(z)` घटकों के साथ रेखीय संवेग `vecp` हो।
View Solutionएक द्रव्यमान M, x-अक्ष के समानान्तर किसी नियत वेग से गति कर रहा है। मूल बिन्दु के सापेक्ष इसका कोणीय संवेग-
View Solutionमूल बिन्दु O के सापेक्ष स्थिति `vecr` पर रेखीय संवेग `vecp` वाले m द्रव्यमान के एक कण पर विचार कीजिए माना कि `vecL` मूल बिन्दु के सापेक्ष कण का कोणीय संवेग है। निम्न में से कौन सा समीकरण सही रूप से `vecr, vecp` एवं `vecL` से संबंधित हैं?
View Solutionकिसी कण पर बल `7hati +3hatj-5hatk` कार्यरत है जिसका स्थिति सदिश `hati-hatj+hatk` है। मूल बिन्दु के परितः दिये गये बल का बल आघूर्ण क्या होगा?
View Solutionएक बलयुग्म उत्पन्न करता है-
View Solutionजब किसी निकाय पर कार्य करने वाला बल आघूर्ण शून्य हो तो निम्न में से क्या नियत होगा?
View Solutionकिसी भारहीन डोरी से छोटे से द्रव्यमान m को बाँध दिया जाता है जिसका दूसरा सिरा चित्रानुसार P पर स्थिर है। द्रव्यमान, केन्द्र O एवं नियत कोणीय गति `omega` के साथ x-y तल मे वृत्तीय गति कर रहा है। यदि निकाय के कोणीय संवेग की O एवं P वे परितः गणना की जाती है तथा क्रमश: `vecL_(O)` व `vecL_(P)` के द्वारा दर्शाया जाता है, तब
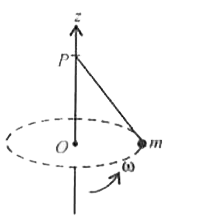
View Solutionनिम्न में से कौन-सा कथन गलत है?
View Solutionकेन्द्रीय बल से घूम रहे किसी कण का कोणीय संवेग किसके कारण नियत होता है?
View Solutionबलयुग्म का आघूर्ण कहलाता है-
View Solutionएक चकती अपने अक्ष के परितः कोणीय वेग `vecomega` से घूम रही है। एक बल `vecF` उस बिन्दु पर कार्यरत है जिसका घूर्णन अक्ष के सापेक्ष स्थिति सदिश `vecr` है। बल के कारण बल आघूर्ण से संबंधित शक्ति को व्यक्त किया जाता है-
View Solutionचित्र, x-y समतल में एक पटल दर्शाता है। दो अक्ष z व z' अपने तल के लम्बवत् गुजरते हैं। दर्शाए गए अनुसार बिन्दु P पर पटल के तल में एक बल F कार्यरत है। निम्न में से कौन-सा कथन गलत है?
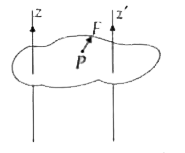
(बिन्दु P, z-अक्ष की अपेक्षा z'- अक्ष के अधिक समीप है)।
View Solutionकिसी कण की स्थिति. `vecr=hati +2hatj-hatk` द्वारा दी गई है तथा इसका रेखीय संवेग, `vecp=3hati +4hatj-2hatk` द्वारा दिया गया है, तो मूल बिन्दु के परितः इसका कोणीय संवेग किसके लम्बवत् होगा?
View Solutionकिसी निकाय के द्रव्यमान केन्द्र का वेग नियत रहता है, यदि निकाय पर कार्यरत कुल बाह्य बल है-
View Solutionयदि `vecF`, स्थिति सदिश `vecr` वाले किसी कण पर कार्यरत बल है तथा `vectau` मूल बिन्दु के परितः इस बल का बल आघूर्ण है, तो
View Solution1 मी लम्बाई तथा 4 किग्रा द्रव्यमान की किसी एकसमान छड़ को 10 सेमी की दूरी पर रखे गए दो चाकुओं के सिरों पर रखा जाता है। एक सिरे से 30 सेमी की दूरी पर 60 N के भार को निलंबित किया जाता है। चाकुओं के सिरों पर प्रतिक्रियाएँ होती हैं-
View Solutionभार W एवं लम्बाई L की एक असमान छड़, चित्र में दिखाए गये अनुसार नगण्य भार की दो डोरियों द्वारा लटकी हुई हैं। ऊर्ध्वाधर से डोरियों द्वारा बनाये गये कोण क्रमश: `theta_(1)` व `theta_(2)` हैं। अपने बायें सिरे से छड़ के गुरुत्वीय केन्द्र की दूरी d है-
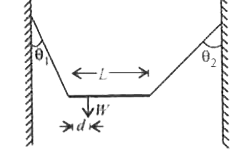
View Solution(1) किसी वस्तु का गुरुत्व केन्द्र वह बिन्दु होता है जिस पर वस्तु का भार कार्य करता है।
(2) द्रव्यमान केन्द्र, गुरुत्वीय केन्द्र के संपाती होगा यदि पृथ्वी की त्रिज्या को अनंत रूप से बड़ा माना जाए।
(3) किसी बाहरी बिन्दु पर किसी पिण्ड के कारण गुरुत्वीय क्षेत्र की तीव्रता का आकलन करने के लिए, पिण्ड के सम्पूर्ण द्रव्यमान को इसके गुरुत्वीय केन्द्र पर संकेंद्रित माना जा सकता है।
(4) किसी अक्ष के परितः घूमने वाले किसी पिण्ड की घूर्णन त्रिज्या, उस पिण्ड के गुरुत्व केन्द्र से अक्ष पर डाले गए लम्ब की लंबाई होती है।
निम्न में से कथनों का कौन-सा युग्म सही है?
View Solutionएक दृढ़ पिण्ड आंशिक साम्य में कहा जाता है, जब वह होता है-
View Solutionएक कार का भार 1800 किग्रा है। इसके सामने तथा पीछे के धुरों के मध्य की दूरी 1.8 मी है। इसका गुरुत्व केन्द्र इसके आगे की धुरी से 1 मी पीछे है। इसके प्रत्येक अगले व पिछले पहिए पर समतल मैदान (Level ground) के द्वारा लगाया गया बल होता है-
(`g= 10` मी सेकण्ड`""^(2)`)
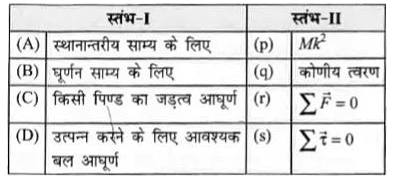
View SolutionM द्रव्यमान तथा a भुजा का एक एकसमान घन घर्षणरहित क्षैतिज पृष्ठ पर रखा गया है। चित्र के अनुसार एक ऊर्ध्वाधर बल किनारे पर आरोपित किया जाता है।
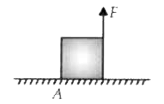
स्तंभ-1 से स्तंभ-II को मिलाएं।
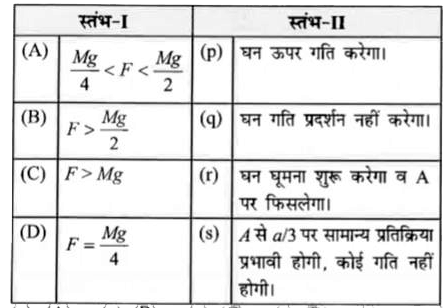
View Solutionनिम्न में से कौन-सा सम्बन्ध सही है?
View Solutionएक मीटर छड़ी को चाकू के सिरे पर इसके केन्द्र पर संतुलित किया गया है। जब दो 5-5 ग्राम वाले सिक्कों में से प्रत्येक को एक के ऊपर एक के रूप में 12 सेमी के चिन्ह पर रखा गया, तो उस छड़ी को 45 सेमी पर संतुलित पाया गया। मीटर-छड़ी का द्रव्यमान है-
View Solutionएक एकसमान 3 मीटर लंबी व 20 किग्रा भार वाली सीढ़ी एक घर्षणरहित दीवार पर झुकी हुई है। इसका निचला भाग खुरदुरे फर्श पर दीवार से 1 मीटर की दूरी पर स्थित है। दीवार एवं फर्श के प्रतिक्रियात्मक बल हैं-
View Solution2L लम्बाई की एक दृढ़ छड़ पर कुछ बल कार्यरत हैं। F नामांकित किए गए सभी बलों का परिमाण समान है। किस प्रकरण में एक अशून्य शुद्ध बल आघूर्ण इसके केन्द्र के परितः छड़ पर कार्यरत है?
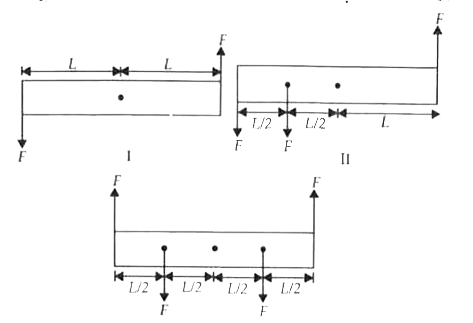
View Solutionघूर्णी गति में द्रव्यमान के सदृश्य है-
View Solutionएक व्यक्ति अपने हाथों में धातु के गोलों के साथ एक घूमती हुई मेज पर खड़ा है। यदि वह अपने हाथों को खींचकर वापस छाती की ओर लाता है, तो उसके कोणीय वेग पर प्रभाव होगा-
View Solutionकिसी पिण्ड का जड़त्व आघूर्ण निर्भर करता है-
View Solutionगोले की स्पर्श रेखा के परितः द्रव्यमान M एवं त्रिज्या R के किसी ठोस गोले का जड़त्व आघूर्ण क्या है?
View SolutionM द्रव्यमान तथा R त्रिज्या का एक ठोस बेलन कोणीय चाल `omega` से अपने अक्ष के परितः घूमता है। इसकी घूर्णी गतिज ऊर्जा क्या है?
View Solutionस्तंभ-I से स्तंभ-II को मिलाइए।
View Solutionभुजा a व b की एक एकसमान आयताकार प्लेट R तथा भुजा c की एक वर्गाकार प्लेट S चित्र में दिखाये गये अनुसार द्रव्यमान व क्षेत्रफल में समान हैं, तो
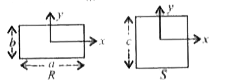
(i) `(I_(xR))/(I_(xS)) lt 1` (ii) `(I_(yR))/(I_(yS)) gt 1`
उपरोक्त कौन-सा सम्बन्ध सही है?
View SolutionM द्रव्यमान वाले दो द्रव्यमानों को L लम्बाई की एक दृढ़-द्रव्यमान हीन छड़ के सिरे से जोड़ा जाता है। तब निकाय का इसके द्रव्यमान केंद्र से गुजरने वाले अक्ष के परितः तथा इसकी लम्बाई के लम्बवत् जड़त्व आघूर्ण होता है-
View Solutionकिसी l लम्बाई की एकसमान छड़ का इसके एक सिरे से गुजरने वाले अक्ष के परितः तथा इसकी लाबाई के लंबवत् घूर्णन त्रिज्या होती है-
View Solutionभुजा a तथा द्रव्यमान m के एक घन के चित्र के संदर्भ से, निम्न में से कौन-सा कथन गलत है?
(O घन का केन्द्र है)
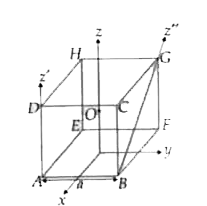
View Solutionकिसी R त्रिज्या तथा 9 M द्रव्यमान की एक वृत्ताकार चकती से, चित्रानुसार, `R // 3` त्रिज्या वाली एक छोटी सी चकती को हटाया जाता है। तब शेष चकती का इसके तल के लम्बवत् तथा O से गुजरने वाले अक्ष के परितः जड़त्व आघूर्ण होता है
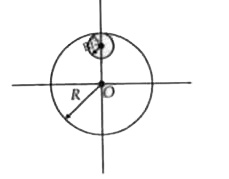
View Solutionनिम्न में से किसका जड़त्व आघूर्ण अधिकतम है जब उनमें से प्रत्येक का द्रव्यमान एवं त्रिज्या समान हो?
View Solution420 rpm की गति से घूमने वाला एक चक्का (Flywheel) `2 rad s^(-2)` की स्थिर दर पर रुक जाता है। इस चक्के को रुकने में लगा समय होता है-
View Solutionएक खिलाड़ी किसी चक्के (Discus) को विराम से `15 rad s^(-1)` के अंतिम कोणीय वेग से 0.270 सेकेण्ड में उसे छोड़ने से पूर्व फेंकता है। त्वरण के दौरान, चक्का 0.810 मीटर त्रिज्या वाले एक वृत्ताकार चाप में गति करता है। चक्के का छूटने से पूर्व त्वरण होता है-
View Solutionएक नगण्य द्रव्यमान की डोरी को 20 किग्रा द्रव्यमान तथा 20 सेंटीमीटर त्रिज्या वाले गतिपालक चक्र पहिए के रिम के चारों ओर लपेटा जाता है। डोरी पर 25 N के स्थायी खिंचाव को लगाया जाता है। खिंचाव के द्वारा किया गया कार्य तब क्या होगा जब 2 मीटर डोरी खोलनी (Unwound) हो?
View Solutionप्रश्न संख्या 58 में, यदि पहिया विरामावस्था से प्रारंभ करता है, पहिया की गतिज ऊर्जा क्या होगी जब 2 मीटर डोरी को खोलना हो?
View Solutionकिसी मोटर के पहिये की कोणीय चाल 16 सेकण्ड में 1200 rpm से 3120 rpm तब बढ़ जाती है। मोटर के पहिए का कोणीय त्वरण
View Solution1800 rpm की गति से घुमाने पर एक ऑटोमोबाइल इंजन 100 kW उत्पन्न करता है। इंजन के द्वारा उत्पन्न बल आघूर्ण होगा-
View Solution3 किग्रा द्रव्यमान एवं 40 सेमी त्रिज्या के किसी खोखले बेलन के चारों ओर एक नगण्य द्रव्यमान की रस्सी लपेटी गई है। यदि रस्सी को 30 N के बल से खींचा जाए तो बेलन में उत्पन्न कोणीय त्वरण क्या होगा?
View Solution3kg द्रव्यमान तथा 40 cm त्रिज्या की किसी खोखले सिलिंडरपर कोई नगण्य द्रव्यमान की रस्सी लपेटी है । यदि रस्सी को 30 N बल से खींचा जाये तो सिलिंडर का कोणीय त्वरण क्या होगा ? रस्सी का रैखिक त्वरण क्या है ? यह मानिये कि इस प्रकरण में फिसलन नहीं है ।
View Solutionकिसी सिल बट्टे (Grindstone) का जड़त्व आघूर्ण `6 kg m^(2)` है। एक नियत बल आघूर्ण को आरोपित करने पर सिल बट्टे को विरामावस्था से शुरू करने के 10 सेकण्ड के बाद 150 rpm की गति मिलती है। बल आघूर्ण होगा-
View Solutionद्रव्यमान M एवं त्रिज्या R वाली एक एकसमान चकती अपने रिम (Rim) पर टेबल पर रखी है। चकती तथा टेबल के मध्य घर्षण गुणांक `mu` है।
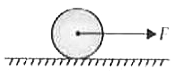
अब डिस्क को चित्र में दर्शाए गए अनुसार बल F से खींचा जाता है। F का वह अधिकतम मान क्या होगा जिसके लिए चकती बिना फिसले घूमती है?
View Solutionकिसी घूर्णक (रोटर) की 100 रेडियन प्रति सेकण्ड एकसमान कोणीय चाल बनाए रखने के लिए एक इंजन द्वारा 100 न्यूटन मीटर का बल आघूर्ण प्रेषित करना आवश्यक होता है। इंजन की शक्ति ज्ञात कीजिए।
View Solutionद्रव्यमान M एवं त्रिज्या R का एक खोखला बेलन अपने सममित अक्ष के परितः घूर्णन कर रहा है तथा समान द्रव्यमान एवं त्रिज्या का एक ठोस गोला इसके केन्द्र से जाने वाली अक्ष के परितः घूर्णन कर रहा है। यदि समान परिमाण का बल आघूर्ण इन पर लगाया जाता है, तो कोणीय त्वरणों का अनुपात क्या होगा?
View Solutionकिसी घूर्णन करते हुए पहिए के किसी बिन्दु पर तात्क्षणिक कोणीय स्थिति को समीकरण `0(t)=2t^(3)-6t^(2)` के द्वारा व्यक्त किया जाता है। पहिए पर बल आघूर्ण इस पर शून्य हो जाएगा-
View Solutionएक वृत्ताकार प्लेटफॉर्म को किसी ऊर्ध्वाधर घर्षणरहित धुरी पर चढ़ाया जाता है। इसकी त्रिज्या r = 2 मी एवं इसका जड़त्व आपूर्ण I = 200 किग्रा `"मी"^(2)` है। यह आरंभ में विराम में रहता है। एक 70 किग्रा भार वाला व्यक्ति प्लेटफॉर्म के सिरे पर खड़ा होता है तथा उसके किनारे के साथ-साथ `v_(0)= 1 "मी से"^(-1)` की चाल से जमीन के सापेक्ष चलना शुरू करता है। प्लेटफॉर्म का कोणीय वेग है-
View Solution20 किग्रा द्रव्यमान एवं 20 सेमी त्रिज्या का कोई ठोस बेलन अपने अक्ष के परितः 100 रेडियन प्रति सेकण्ड की कोणीय चाल से घूर्णन कर रहा है। अपने अक्ष के परितः बेलन का कोणीय सवेग क्या है?
View Solutionजब कोई द्रव्यमान किसी निश्चित बिन्दु के परितः किसी समतल में घूर्णन कर रहा होता है, तब उसका कोणीय संवेग निम्न में से किसके निर्दिष्ट होता है?
View Solution`I_(1)` एवं `I_(2)` जड़त्व आघूर्णों वाली दो चकतियाँ अपने-अपने अक्षों के परितः (चकती के समकोण पर तथा केन्द्र से होकर गुजरते हुए) क्रमश: `omega_(1)` एवं `omega_(2)` कोणीय चालों से घूर्णन कर रही हैं। जब उन्हें उनके घूर्णन-संपातन अक्षों (Axes of rotation coincident) के साथ आमने-सामने लाया जाता है, तो इस प्रक्रिया में निकाय (System) की गतिज ऊर्जा में हास क्या होगा?
View Solutionएक व्यक्ति, एक घूमने वाले स्टूल पर हाथ फैलाकर चक्रण कर रहा है। वह अचानक अपने हाथों को नीचे कर लेता है। निम्न में से उसकी गतिज ऊर्जा K एवं कोणीय संवेग L के बारे में कौन सा कथन सही है?
View Solutionएक लड़का एक घूमने वाले मेज के केन्द्र पर दोनों हाथ फैलाकर इस प्रकार खड़ा है कि वह कोणीय चाल `omega_(0)` से अपने केन्द्रीय अक्ष के परितः घूर्णन कर रहा है। अब, वह लड़का अपने हाथों को पीछे मोड़ लेता है ताकि जड़त्व आघूर्ण प्रारंभिक मान से 3 गुना हो जाए। नई कोणीय चाल क्या होगी?
View Solutionनिम्न में से कौन-से सिद्धांत को सर्कस में करतब दिखाने वाले लोग अपनाते हैं?
View Solutionकिसी दृढ़ पिण्ड का कोणीय संवेग L एवं घूर्णन गतिज ऊर्जा `K_(R)` किस सम्बन्ध द्वारा एक-दूसरे से सम्बन्धित हैं?
(I= जड़त्व आघूर्ण)
View Solutionसामान्यतः चक्के का द्रव्यमान उसकी रिम में केन्द्रित होता है, क्योंकि
View Solutionघूर्णन पिण्ड का कुल कोणीय संवेग नियत रहता है, यदि पिण्ड पर कार्यरत कुल बल आघूर्ण है-
View Solutionदिया गया चित्र दो समरूप कणों 1 व 2 को दर्शाता है, जिनमें से प्रत्येक का द्रव्यमान m है तथा जो समानान्तर रेखाओं के अनुदिश विपरीत दिशाओं में समान गति `vecv` से गति कर रहे हैं।
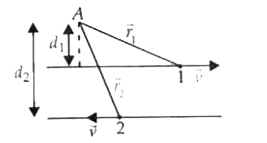
किसी विशेष क्षण पर, `vecr_(1)` एवं `vecr_(2)` बिन्दु A से डाले गए उनके संगत स्थिति सदिश हैं जो समानान्तर रेखाओं के तल में है। निम्न में से कौन-सा कथन सही है?
View Solution`I_(1)` एवं `I_(2)` जड़त्व आघूर्णों वाली दो चकतियाँ अपने संगत अक्षों के परितः क्रमशः `omega_(1)` व `omega_(2)` कोणीय आवृत्तियों के साथ घूम रही हैं। जब उन्हें उनके घूर्णन-संपातन अक्षों के साथ आमने-सामने लाया जाता है, तो संयुक्त चकती (Composite disc) की कोणीय आवृत्ति होगी-
View Solutionएक नाट्य नर्तकी, किसी चिकने फर्श पर अपनी बाहों को पास लाकर ऊर्ध्वाधर अक्ष के परित: `20 rad // s` के कोणीय वेग से चक्रण (Spinning) कर रही है। जब वह अपनी बांहों को पूर्णतया फैला लेती है, तो चक्रण की गति घटकर `10 rad // s` हो जाती है। यदि नर्तकी का आरंभिक जड़त्व आघूर्ण है `I`, तो नया जड़त्व आघूर्ण होगा-
View Solutionएक लड़का अपनी केन्द्रीय अक्ष के परितः घूर्णन कर रहे प्लेटफॉर्म के केन्द्र पर हाथों को मोड़कर खड़ा है। निकाय की गतिज ऊर्जा K है। अब, लड़का अपनी भुजाओं को फैला देता है ताकि निकाय का जड़त्व आघूर्ण दुगुना हो जाए। अब, निकाय की गतिज ऊर्जा क्या होगी?
View Solutionएक व्यक्ति किसी घूमते हुए प्लेटफॉर्म पर अपने प्रत्येक हाथ में 5 किग्रा भार वाले गोलों को पकड़कर बाँहें फैलाकर खड़ा है। प्लेटफॉर्म की कोणीय चाल 1.2 `"परिक्रमण" // "सेकण्ड"^(-1)` है। प्लेटफॉर्म के साथ व्यक्ति के जड़त्व आघूर्ण को नियत तथा 6 किग्रा `"मी"^(2)` के बराबर माना जा सकता है। यदि वह व्यक्ति अक्ष से दोनों भारों की दूरी को 100 सेमी से कम करके 20 सेमी तक लाकर अपनी बाँहों को छाती के पास ले आता है, तो प्लेटफॉर्म की नई कोणीय चाल होगी-
View Solutionदो पिण्डों के जड़त्व आघूर्ण अपनी घूर्णन अक्ष के परि क्रमशः I एवं 2I हैं। यदि उनकी घूर्णन गतिज ऊर्जाएं बराबर हैं, तो उनके कोणीय संवेगों का अनुपात क्या होगा?
View Solutionएक ठोस गोला समान ऊँचाई लेकिन झुकाव के विभिन्न कोणों वाले दो विभिन्न नत समतलों (Inclined planes) से नीचे लुढ़कता है। दोनों ही प्रकरणों में-
View Solution5 किग्रा द्रव्यमान एवं 0.40 मी. त्रिज्या वाला पहिया बिना फिसले सड़क पर कोणीय वेग 10 रेडियन सेकण्ड`""^(-1)` के साथ चल रहा है। घूर्णन अक्ष के परितः पहिए का जड़त्व आघूर्ण 0.65 किग्रा/ मी`""^(2)` है। पहिए की कुल गतिज ऊर्जा में घूर्णन की गतिज ऊर्जा का प्रतिशत है-
View Solutionतीन पिण्ड, वलय, ठोस बेलन एवं ठस गोले को बिना फिसले नत समतल से नीचे लुढ़काया जाता है। ये विरामावस्था से प्रारंभ करते हैं। पिण्डों की त्रिज्याएं समरूप हैं। कौन-सा पिण्ड अधिकतम वेग से नीचे पहुँचता है?
View Solutionएक ठोस बेलन `theta` झुकाव वाले किसी नत समतल पर आरंभिक वेग v के साथ लुढ़कता है। बेलन तल पर कितनी दूरी पर जाता है?
View SolutionR त्रिज्या की वलय क्षैतिज अक्ष के परितः कोणीय चाल `omega_(0)` से घूर्णन कर रही है। इसे खुरदरे क्षैतिज मेज पर रखा जाता है। गतिज घर्षण गुणांक `mu_(k)` है। वह समय क्या होता है जिसके पश्चात् यह लुढ़कना शुरू करती है?
View Solution2 मी त्रिज्या एवं 100 किग्रा भार वाला एक घेरा (Hoop) एक क्षैतिज फर्श के साथ इस प्रकार से लुढ़कता है ताकि इसके द्रव्यमान केन्द्र की गति 20 `"सेमी" // "से"` हो जाए। इसे रोकने के लिए कितना कार्य करना पड़ेगा?
View Solutionठोस बेलन `theta` झुकाव एवं स्थैतिक घर्षण गुणांक `mu_(s)` वाले समतल पर बिना फिसले लुढ़क रहा है। `theta` एवं `mu_(s)` सम्बन्ध है-
View Solutionजब कोई ठोस गोला क्षैतिज के साथ `theta` कोण बनाते हुए किसी नत समतल से बिना फिसले लुढ़कता है, तो इसके द्रव्यमान केन्द्र का त्वरण a है। यदि यही गोला बिना घर्षण के लुढ़कता है, तो इसका त्वरण a' होगा-
View SolutionM द्रव्यमान एवं R त्रिज्या का एक एकसमान गोला किसी खुरदरे क्षैतिज पृष्ठ (चित्र) पर रखा है। गोला तल से h ऊँचाई पर क्षतिज रूप से टकराता है।
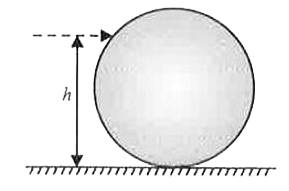
स्तंभ-I से स्तंभ-II को मिलाइए।
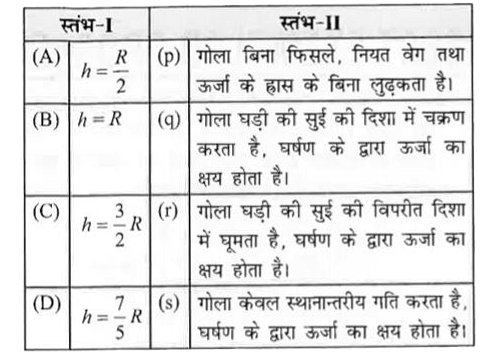
View Solutionनिम्न में से कौन-सा कथन गलत है?
View Solutionएक पिण्ड किसी नत समतल से नीचे की ओर लुढ़क रहा है। यदि घूर्णन को गतिज ऊर्जा, स्थानान्तरीय अवस्था में गतिज ऊर्जा की 40% है, तो पिण्ड होता है-
View SolutionM द्रव्यमान एवं R त्रिज्या का एक ठोस बेलन क्षैतिज से `theta` कोण बनाते हुए नत समतल से नीचे बिना फिसले लुढ़कता है। तो इसका त्वरण क्या होगा?
View Solutionप्रश्न संख्या 96 में, बेलन पर कार्यरत घर्षण बल होता है जब एक ठोस सिलेंडर झुकाव के एक झुकाव वाले विमान को लुढ़कता है θ क्षैतिज के साथ।-
View Solutionएक गेंद बिना फिसले लुढ़कती है। इसके द्रव्यमान केन्द्र से गुजरने वाले अक्ष के परितः गेंद की घूर्णन त्रिज्या k है। यदि गेंद की त्रिज्या R हो, तो कुल ऊर्जा का अंश इसके घूर्णन से संबंधित होगा-
View Solutionदो घूर्णन पिण्ड A एवं B के जड़त्व आघूर्ण `I_(A)` एवं `I_(B)` (`I_(A) gt I_(B)`) हैं। यदि इनके कोणीय संवेग बराबर हों, तो-
View Solutionनिम्न में से कौन-सा कथन सही नहीं है?
View Solution
बहुविकल्प प्रश्न पिटारा questions and complete solutions for chapter कणों के निकाय घूर्णी गति of MTG PHYSICS (HINDI) of Class 11