Complete Solutions to उदाहरण of chapter सरल रेखाएँ of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | सरल रेखाएँ |
| NCERT HINDI | उदाहरण |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
उन रेखाओ के ढाल ज्ञात कीजिए जो
`(3 , -2 )` और `(-1 ,4 )` बिन्दुओ से होकर जाती है ,
View Solutionउन रेखाओ के ढाल ज्ञात कीजिए जो
`(3 ,-2 )` और `(7 ,-2 ) ` बिन्दुओ से होकर जाती है,
View Solutionउन रेखाओ के ढाल ज्ञात कीजिए जो
`(3 ,-2 ) ` और `(3 ,4 )` बिन्दुओ से होकर जाती है ,
View Solutionउन रेखाओ के ढाल ज्ञात कीजिए जो
धन x -अक्ष से `60 ^(@)` का कोण बनाती है।
View Solutionयदि दो रेखाओ के बिच का कोण `pi /4 ` है और एक रेखा की ढाल `1 /2 ` है तो दूसरी रेखा की ढाल ज्ञात कीजिए।
View Solution`(-2 ,6 ) ` और `(4 ,8 )` बिन्दुओ को मिलाने वाली रेखा, `(8 ,12 )` और `(x , 24 )` बिन्दुओ को मिलनेवाली रेखा पर लांब है। x का मान ज्ञात कीजिए।
View Solutionतीन बिंदु `P (h ,K ), Q (x _(y ) y _(1 ))` और `R (x _(2 ) y _(2 ))` एक रेख पर है दिखाइए `(h-x_(1)) (y_(2) -y_(1)) =(k - y _(1)) (x_(2) -x_(1))`
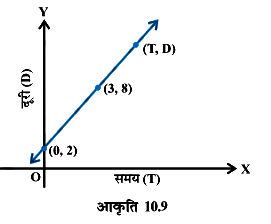
View Solutionआकृति `10 *9 ` में एक रेखिक गति का समय और दुरी का लेखाचित्र दिया है समय और दुरी की दो स्थितियॉं जब `T =0 ,D =2 ` और जब `T =3 ,D =8 ` अंकित की गई है । ढाल की सकल्पना का प्रमेय करके गति का नियम ज्ञात कीजिए अर्थात दुरी, समय पर किस प्रकार आश्रित है।
View Solutionअक्षो के समान्तर और `(-2 ,3 )` से जाने वाली रेखाओ के समीकरण ज्ञात कीजिए।
View Solution`(-2 ,3 )` से जाने वाली ढाल -4 की रेखा का समीकरण ज्ञात कीजिए।
View Solutionबिन्दुओ `(1 ,-1 )` और `(3 ,5 )` से होकर जाने वाली रेखा का समीकरण लिखिए।
View Solutionउन रेखाओ के समीकरण लिखित जनके लिए `tan theta =1 /2 ,` जहां `theta ` रेखा का झुकाव है और (i )y -अंत, खंड `- 3 /2 ` है, (ii ) x -अंत,खंड 4 है ।
View Solutionएक रेखा का समीकरण ज्ञात कीजिए जो x और y -अक्ष क्रमशः -3 और 2 के अंत,खंड बनाती है ।
View Solutionरेखा का समीकरण ज्ञात कीजिए जिसकी मूल बिंदु से लंबिक दुरी 4 इकाई और धन x -अक्ष तथा लंब के बिच कोण `15^(@)` है।
View Solutionफारेनहाइट ताप F और परम तप K एक रैखिक समीकरण को संतुष्ट करते है। दिया है कि `K =273 ` जब `F =32 ` और `K =373 ` जब `F =212 ` तो K को F के पदों में व्यक्त कीजिए और F का मान ज्ञात कीजिए जबकि `K =0 `
View Solutionएक रेखा का समीकरण `3x -4y +10 =0 ` है । इसके (i ) ढाल x -और y -अंत,खंड ज्ञात कीजिए।
View Solutionसमीकरण `sqrt3x+y-8=0` को लंब रूप में रूपांतरित कीजिए और p तथा `omega`के मान ज्ञात कीजिए।
View Solution`y-sqrt3 x-5 =0` और ` sqrt3y-x+6=0` रेखाओ के बिच का कोण ज्ञात कीजिए।
View Solutionदर्शाइए कि दो रेखाएँ `a_(1)x+b_(1)y+c_(1)=0` और `a _(2)x +b_(2)y+c_(2) =0` जहाँ `b _(1)b_(2) ne 0` (i ) समान्तर है यदि `(a_(1))/(b _(1))=(a_(2))/(b_(2))` और (ii ) लंब है यदि `a _(1) a_(2)+ b _(1)b_(2) =0`
View Solutionरेखा `x-2y+3=0` पर लंब और बिंदु `(1,-2)` से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
View Solutionबिंदु `(3,-5)` कि रेखा `3x-4-26=0` से दुरी ज्ञात कीजिए।
View Solutionसमान्तर रेखाओ `3x-4y+7=0` और `3x-4y+5=0` के बिच कि दुरी ज्ञात कीजिए ।
View Solution`2x+y-3=0,5x+ky -3=0` और `3x-y-2=0` संगमि है, तो k का मान ज्ञात कीजिए ।
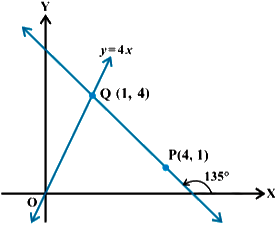
View Solutionबिंदु `P (4 ,1 )` से रेखा `4x -y =0 ` कि दुरी उस रेखा के अनुदिश ज्ञात कीजिए जो धन x -अक्ष से `135 ^(@) ` का कोण बनाती है ।
View Solutionकल्पना करते हुए कि सरल रेखाएँ बिंदु के लिए दर्पण कि तरह कार्य करती है बिंदु (1 ,2 ) का रेखा `x -3y +4 =0 ` में प्रतिबिम्ब ज्ञात कीजिए ।
View Solutionदर्शाइए कि रेखाओ
`y=m_(1) x+c_(1)y=m_(2) x+c_(2)` और `x=0` से बने त्रिभुज का क्षेत्रफल `((c _(1) -c_(2))^(2))/(2।m_(1)-m_(2)।)` है ।
View Solutionएक रेखा इस प्रकार है कि इसका रेखाओ `5x-4+4=0` और `3x+4y-4=0` के बिच का रेखाखण्ड बिंदु `(1 ,5 )` पर समद्विभाजित होता है इनका समीकरण प्राप्त कीजिए।
View Solutionदर्शाइए कि एक गतिमान बिंदु जिनकी दो रेखाओ `3x -2y =5 ` और `3x +2y =5 ` से दूरियां समान है, का पथ-एक रेखा है ।
View Solution
उदाहरण questions and complete solutions for chapter सरल रेखाएँ of NCERT गणित(HINDI) of Class 11