Complete Solutions to SOLVED EXAMPLES of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| Mathematics | SOLVED EXAMPLES |
| Number Of Questions | 22 |
| Academic Year | 2023-24 |
2 Let N be the set of natural numbers. Define a real valued function f : N-> N by f (x) = 2x + 1. Using this definition, complete the table given below.

View SolutionExamine each of the following relations given below and state in each case, giving reasons whether it is a function or not?
(i) R = {(2,1),(3,1), (4,2)},
(ii) R = {(2,2),(2,4),(3,3), (4,4)}
(iii) R = {(1,2),(2,3),(3,4), (4,5), (5,6), (6,7)}
View SolutionDefine the function f : R `->`R by y = f(x) = `x^2`, `x in R`. Complete the Table given below by using this definition. What is the domain and range of this function?

View SolutionLet N be the set of natural numbers and the relation R be defined on N such that `R = {(x , y) : y = 2x , x , y in N}`.What is the domain, codomain and range of R? Is this relation a function?
View SolutionLet `f(x)=sqrt(x)`and `g(x) = x`be two functions defined over the set of nonnegative real numbers. Find `(f + g) (x)`, `(f g) (x)`, `(fg) (x)`and `(f/g)(x)`.
View SolutionLet `f(x)=x^2`and `g(x) = 2x + 1`be two real functions. find `(f +g)(x)`, `(f-g)(x)`, `(fg)(x)`, `(f/g)(x)`.
View SolutionDefine the real valued function `f : R {0} ->R`defined by `f(x)=1/x`,`x in R {0}`. Complete the Table given below using this definition. What is the domain and range of this function?`y=1/x`
View SolutionDraw the graph of the function `f : R-> R`defined by `f(x)=x^3`, `x in R`.
View SolutionLet R be a relation from Q to Q defined by `R={(a,b):a,b in Q and a,b in Z}. Show that `{a,a) in R for all a in Q ,`{a,b} in R implies` that `{b,a} in R, {a,b} in R and {b,c} in R implies that {a,c} in R` `
View SolutionLet R be the set of real numbers. Define the real function `f : R ->Rb y f(x) = x + 10`and sketch the graph of this function.
View SolutionIf `(x + 1, y - 2) = (3, -1)`, find the values of x and y.
View SolutionLet `A= {1, 2, 3}`, `B = {3, 4}`and `C = {4, 5, 6}`. Find(i) `A xx(B nnC)` (ii) `(A xxB) nn(A xxC)`(iii) `A xx(B uuC)` (iv) `(A xxB) uu(A xxC)`
View SolutionIf `P = {a , b , c}`and `A xxB = {(p , q), (p , r), (m , q), (m , r)}``Q = {r}`, form the sets `P xxQ a n d Q xxP`.Are these two products equal?
View SolutionIf R is the set of all real numbers, what do the cartesian products `R xxR`and `R xxR xxR`represent?
View SolutionIf `P = {1, 2}`form the set `P xxP xxP`.
View SolutionThe function f is defined by `f(x) ={[1-x \ x<0], [1 \ \ \ \ \ \ \ \ x=0], [x+1 \ x >0]}`. Draw the graph of `f(x)`.
View SolutionFind the domain of the function `f(x) =(x^2-3x+5)/(x^2-5x+4)`.
View SolutionLet `f = {(1, 2), (2, 3), (0, -1), ( -1, -3)}` be a linear function from Z into Z. Find `f(x)`.
View SolutionIf `A xxB = {(p , q), (p , r), (m , q), (m , r)}`, find A and B.
View SolutionLet `A = {1, 2, 3, 4, 5, 6}`. Define a relation R from A to A by `R = {(x , y) : y = x +1}`(i) Depict this relation using an arrow diagram.(ii) Write down the domain, co-domain and range of R.
View SolutionThe Fig 2.6 shows a relation between the sets P and Q. Write this relation
(i) in set- builder form,
(ii) in roster form.What is its domain and range?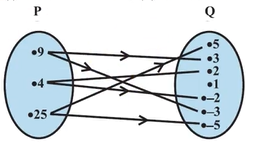
View SolutionLet `A = {1, 2}`and `B = {3, 4}`. Find the number of relations from A to B.
View Solution
SOLVED EXAMPLES questions and complete solutions for chapter RELATIONS AND FUNCTIONS of NCERT MATHEMATICS(HINGLISH) of Class 11