Complete Solutions to Exercise of chapter સુરેખપથ પર ગતિ of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | સુરેખપથ પર ગતિ |
| NCERT | Exercise |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
x-અક્ષને અનુલક્ષીને ગતિ કરતાં એક પદાર્થનું સ્થાન `x = a + bt^(2)` વડે દર્શાવ્યું છે. જ્યાં `a = 8.5 m, b = 2.5 ms^(-2)` અને tનું માપન સેકન્ડમાં કરેલ છે. t = 0 સમયે તેનો વેગ કેટલો હશે ? 2.0 s અને 4.0 s વચ્ચે સરેરાશ વેગ કેટલો હશે ?
View Solutionકલનશાસ્ત્રની રીતનો ઉપયોગ કરીને નિયમિત પ્રવેગી ગતિનાં સમીકરણો મેળવો.
View Solutionએક બહુમાળી મકાનના ટોચ ૫૨થી એક દડાને (Ball) શીરોલંબ ઊર્ધ્વદિશામાં `20 m s^(-1)`ની ઝડપથી ફેંકવામાં આવે છે. દડો જે બિંદુએથી ફેંકવામાં આવે છે તેની જમીન (Ground)થી ઊંચાઈ 25 m છે. દડો કેટલી ઊંચાઈએ પહોંચશે ?
View Solutionએક બહુમાળી મકાનના ટોચ ૫૨થી એક દડાને (Ball) શીરોલંબ ઊર્ધ્વદિશામાં `20 m s^(-1)`ની ઝડપથી ફેંકવામાં આવે છે. દડો જે બિંદુએથી ફેંકવામાં આવે છે તેની જમીન (Ground)થી ઊંચાઈ 25 m છે. દડો જમીનને અથડાય તે પહે લાં કેટલો સમય લાગશે ? `g = 10 m s^(-2)` લો.
View Solutionમુક્તપતન પામતા પદાર્થની ગતિની ચર્ચા કરો. હવાનો અવરોધ અવગણો.
View Solution"સ્થિર સ્થિતિમાંથી મુક્તપતન પામતાં પદાર્થ દ્વારા સમાન સમયગાળામાં કપાયેલ અંતરો એકબીજાના એવા ગુણોત્તરમાં હશે જે ગુણોત્તર 1થી શરૂ થતી એકી સંખ્યા માટે હોય. (એટલે કે 1 : 3 : 5: 7 : .........) તેમ સાબિત કરો.
View Solutionગતિમાન વાહનને બ્રેક લગાડવામાં આવે ત્યારે તે થોભે તે પહેલાં તેણે કાપેલ અંતરને વાહનનું સ્ટોપિંગ ડિસ્ટન્સ કહે છે. રસ્તા પર વાહનોની સલામતી માટે આ એક અગત્યનું પરિબળ છે. Stopping distance વાહનના પ્રારંભિક વેગ, બ્રેકની ક્ષમતા અથવા બ્રેક લગાડવાથી વાહનમાં ઉદ્દ્ભવતા પ્રતિપ્રવેગ (-a) પર આધારિત છે. વાહન `v_0` અને a માટેના પદમાં Stopping distanceનું સૂત્ર મેળવો.
View Solutionબે સમાંતર રેલવે ટ્રેક ઉત્તર દક્ષિણ દિશામાં છે. ટ્રેન A ઉત્તર તરફ `54 km h^(-1)`ની ઝડપે અને ટ્રેન B દક્ષિણ દિશામાં `90 km h^(-1)`ની ઝડપે ગતિ કરે છે. તો, A સાપેક્ષે Bનો વેગ
View Solutionબે સમાંતર રેલવે ટ્રેક ઉત્તર દક્ષિણ દિશામાં છે. ટ્રેન A ઉત્તર તરફ `54 km h^(-1)`ની ઝડપે અને ટ્રેન B દક્ષિણ દિશામાં `90 km h^(-1)`ની ઝડપે ગતિ કરે છે. તો, B સાપેક્ષે જમીનનો વેગ અને.
View Solutionબે સમાંતર રેલવે ટ્રેક ઉત્તર દક્ષિણ દિશામાં છે. ટ્રેન A ઉત્તર તરફ `54 km h^(-1)`ની ઝડપે અને ટ્રેન B દક્ષિણ દિશામાં `90 km h^(-1)`ની ઝડપે ગતિ કરે છે. તો, ટ્રેન Aની છત પર તેની ગતિની વિરુદ્ધ દિશામાં. (ટ્રેન A સાપેક્ષે `18 km h^(-1)`ની ઝડપથી) દોડતાં વાંદરાનો વેગ જમીન પર ઊભી રહેલી વ્યક્તિ સાપેક્ષે શોધો.
View Solutionનીચે આપેલ ગતિનાં ઉદાહરણો પૈકી કયા ઉદાહરણમાં તંત્રને આશરે બિંદુવત પદાર્થ ગણી શકાય ? : બે સ્ટેશન વચ્ચે વગર ઝટકે (jerks) ગતિ કરતી ટ્રેન
View Solutionનીચે આપેલ ગતિનાં ઉદાહરણો પૈકી કયા ઉદાહરણમાં તંત્રને આશરે બિંદુવત પદાર્થ ગણી શકાય ? : સરળતાથી કોઈ વર્તુળમાર્ગ પર સાઇકલ ચલાવતી વ્યક્તિના માથા પર બેઠેલ કોઈ વાંદરો
View Solutionનીચે આપેલ ગતિનાં ઉદાહરણો પૈકી કયા ઉદાહરણમાં તંત્રને આશરે બિંદુવત પદાર્થ ગણી શકાય ? : જમીન પર અથડાઈને તીવ્ર વળાંક લેતો સ્પિન થતો (spining) ક્રિકેટનો દડો
View Solutionનીચે આપેલ ગતિનાં ઉદાહરણો પૈકી કયા ઉદાહરણમાં તંત્રને આશરે બિંદુવત પદાર્થ ગણી શકાય ? : ટેબલની કિનારી પરથી ખસીને પડતું બીકર
View Solutionબે બાળકો A અને B તેમની શાળા Oથી અનુક્રમે તેમના ઘરે P અને Q પરત ફરી રહ્યાં છે. જેનો સ્થાન-સમય (x – t) આલેખ આકૃતિ 3.19માં દર્શાવેલ છે. નીચે કૌંસમાં દર્શાવેલ સાચી નોંધ પસંદ કરો.
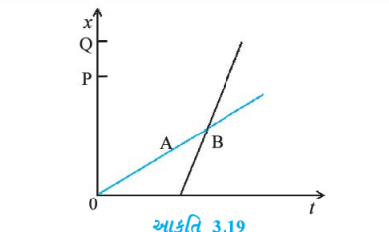 (B/A), (A/B) કરતાં શાળાની નજીક રહે છે.
(B/A), (A/B) કરતાં શાળાની નજીક રહે છે.
View Solutionબે બાળકો A અને B તેમની શાળા Oથી અનુક્રમે તેમના ઘરે P અને Q પરત ફરી રહ્યાં છે. જેનો સ્થાન-સમય (x – t) આલેખ આકૃતિ 3.19માં દર્શાવેલ છે. નીચે કૌંસમાં દર્શાવેલ સાચી નોંધ પસંદ કરો.
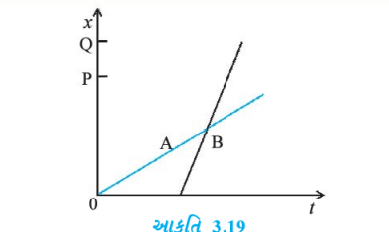 (B/A), (A/B) કરતાં શાળાએથી વહેલી શરૂઆત કરે છે.
(B/A), (A/B) કરતાં શાળાએથી વહેલી શરૂઆત કરે છે.
View Solutionબે બાળકો A અને B તેમની શાળા Oથી અનુક્રમે તેમના ઘરે P અને Q પરત ફરી રહ્યાં છે. જેનો સ્થાન-સમય (x – t) આલેખ આકૃતિ 3.19માં દર્શાવેલ છે. નીચે કૌંસમાં દર્શાવેલ સાચી નોંધ પસંદ કરો.
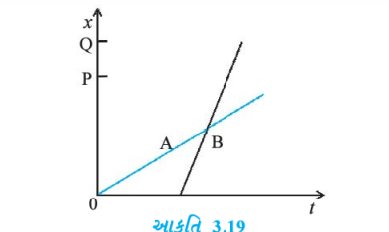 (B/A), (A/B) કરતાં ઝડપથી ચાલે છે.
(B/A), (A/B) કરતાં ઝડપથી ચાલે છે.
View Solutionબે બાળકો A અને B તેમની શાળા Oથી અનુક્રમે તેમના ઘરે P અને Q પરત ફરી રહ્યાં છે. જેનો સ્થાન-સમય (x – t) આલેખ આકૃતિ 3.19માં દર્શાવેલ છે. નીચે કૌંસમાં દર્શાવેલ સાચી નોંધ પસંદ કરો.
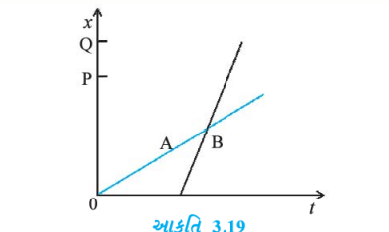 A અને B એક જ જુદા જુદા સમયે ઘરે પહોંચે છે.
A અને B એક જ જુદા જુદા સમયે ઘરે પહોંચે છે.
View Solutionબે બાળકો A અને B તેમની શાળા Oથી અનુક્રમે તેમના ઘરે P અને Q પરત ફરી રહ્યાં છે. જેનો સ્થાન-સમય (x – t) આલેખ આકૃતિ 3.19માં દર્શાવેલ છે. નીચે કૌંસમાં દર્શાવેલ સાચી નોંધ પસંદ કરો.
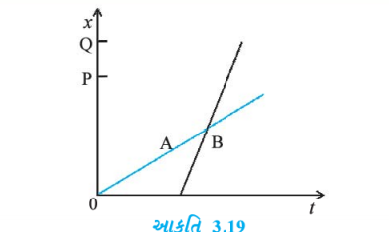 (A/B) રસ્તા પર (B/A)થી (એક વખત/ બે વખત) આગળ નીકળી જાય છે.
(A/B) રસ્તા પર (B/A)થી (એક વખત/ બે વખત) આગળ નીકળી જાય છે.
View Solutionએક જેટ પ્લેન `500 km h^(-1)`ની ઝડપે ઊડી રહ્યું છે, અને તે જેટ પ્લેનની સાપેક્ષે `1500 km h^(-1)`ની ઝડપે દહન-ઉત્પાદનો (વાયુ)ને બહાર કાઢી રહ્યું છે. જમીન પર ઊભેલા કોઈ અવલોકનકારની સાપેક્ષે દહન- ઉત્પાદનોની ઝડપ કેટલી હશે ?
View Solutionસુરેખ રાજમાર્ગ પર `126 km h^(-1)` જેટલા ઝડપે દોડી રહેલી એક કાર 200 m અંતર કાપીને ઊભી રાખવી છે તો કારનો નિયમિત પ્રતિપ્રવેગ કેટલો હોવો જોઈએ ? કારને સ્થિર થવા માટે કેટલો સમય લાગશે ?
View Solution400 m જેટલી સમાન લંબાઈ ધરાવતી બે ટ્રેનો A અને B બે સમાંતર રેલવે ટ્રેક પર `72 km h^(-1)`ની ઝડપે એક જ દિશામાં દોડી રહી છે. ટ્રેન A, ટ્રેન B કરતાં આગળ છે. B ટ્રેનનો ડ્રાઇવર ટ્રેન Aને ઓવરટેક કરવાનું વિચારે છે અને પોતાની ટ્રેનને `1 m s^(-2)` જેટલી પ્રવેગિત કરે છે. જો 50 s બાદ ટ્રેન Bનો ગાર્ડ ટ્રેન Aના ડ્રાઇવરની આગળ થઈ જાય છે, તો તેમની વચ્ચેનું પ્રારંભિક અંતર કેટલું હશે ?
View Solutionએક દ્વિમાર્ગી (two-lane road) રસ્તા પર કાર A `36 km h^(-1)`ની ઝડપે ગતિ કરે છે. એકબીજાની વિરુદ્ધ દિશામાં `54 km h^(-1)` જેટલી સમાન ઝડપથી દોડતી કાર B અને C કાર A સુધી પહોંચવાનોપ્રયત્ન કરે છે. કોઈ એક ક્ષણે AB તથા AC વચ્ચેનું સમાન અંતર 1 km છે. આ ક્ષણે કાર Bનો ડ્રાઇવર, કાર C, કાર Aને ઓવરટેક કરે તે પહેલાં ઓવરટેક કરવાનું વિચારે છે, તો અકસ્માત-નિવારણ માટે કાર Bનો લઘુતમ પ્રવેગ કેટલો હોવો જોઈએ ?
View Solutionકોઈ એક ખેલાડી `29.4 m s^(-1)`ની પ્રારંભિક ઝડપથી એક દડાને ઊર્ધ્વદિશામાં ફેંકે છે. દડાની ઊર્ધ્વદિશાની ગતિ દરમિયાન પ્રવેગની દિશા કઈ હશે ?
View Solutionકોઈ એક ખેલાડી `29.4 m s^(-1)`ની પ્રારંભિક ઝડપથી એક દડાને ઊર્ધ્વદિશામાં ફેંકે છે. તેની ગતિના મહત્તમ ઊંચાઈવાળા બિંદુએ દડાનો વેગ અને પ્રવેગ કેટલા હશે ?
View Solutionકોઈ એક ખેલાડી `29.4 m s^(-1)`ની પ્રારંભિક ઝડપથી એક દડાને ઊર્ધ્વદિશામાં ફેંકે છે. દડાની મહત્તમ ઊંચાઈવાળા બિંદુએ સ્થાન x = 0 m અને t = 0 s તથા શિરોલંબ નીચે તરફની દિશાને x-અક્ષની ધન દિશા તરીકે પસંદ કરો. આ પસંદગીના સંદર્ભે દડાની ઊર્ધ્વદિશાની ગતિ અને અધોદિશાની ગતિ માટે સ્થાન, વેગ અને પ્રવેગનાં ચિહ્નો દર્શાવો.
View Solutionકોઈ એક ખેલાડી `29.4 m s^(-1)`ની પ્રારંભિક ઝડપથી એક દડાને ઊર્ધ્વદિશામાં ફેંકે છે. દડો કેટલી મહત્તમ ઊંચાઈએ પહોંચશે ? અને કેટલા સમય બાદ ખેલાડીના હાથમાં પાછો આવશે ? (`g = 9.8 m s^(-2)` અને વાયુનો અવરોધ અવગણીએ છીએ.)
View Solutionનીચે આપેલ કથનોને ધ્યાનપૂર્વક વાંચી ઉદાહરણ અને કારણ સહિત તે સાચાં છે કે ખોટાં તે દર્શાવો કણની એક પારિમાણિક ગતિમાં, કોઈ એક ક્ષણે તેની ઝડપ શૂન્ય હોવા છતાં તેનો પ્રવેગ અશૂન્ય હોઈ શકે છે.
View Solutionનીચે આપેલ કથનોને ધ્યાનપૂર્વક વાંચી ઉદાહરણ અને કારણ સહિત તે સાચાં છે કે ખોટાં તે દર્શાવો કણની એક પારિમાણિક ગતિમાં,ઝડપ શૂન્ય હોવા છતાં તેનો વેગ અશૂન્ય હોઈ શકે.
View Solutionનીચે આપેલ કથનોને ધ્યાનપૂર્વક વાંચી ઉદાહરણ અને કારણ સહિત તે સાચાં છે કે ખોટાં તે દર્શાવો કણની એક પારિમાણિક ગતિમાં, ઝડપ અચળ હોય, તો પ્રવેગ હંમેશાં શૂન્ય હોય.
View Solutionનીચે આપેલ કથનોને ધ્યાનપૂર્વક વાંચી ઉદાહરણ અને કારણ સહિત તે સાચાં છે કે ખોટાં તે દર્શાવો કણની એક પારિમાણિક ગતિમાં, પ્રવેગના ધન મૂલ્ય માટે ગતિ વધતી હોય છે.
View Solutionઉદાહરણ સહિત બંને તફાવત સ્પષ્ટ કરો. કોઈ એક સમયગાળામાં સ્થાનાંતરનું માન (જેને ઘણી વાર અંતર પણ કહે છે.) અને કોઈ કણ દ્વારા આટલા જ સમયગાળામાં કાપેલ કુલ પથલંબાઈ
View Solutionઉદાહરણ સહિત બંને તફાવત સ્પષ્ટ કરો. કોઈ એક સમયગાળામાં સરેરાશ વેગનું માન અને એટલા જ સમયગાળા માટે સરેરાશ ઝડપ [આપેલ સમયગાળા માટે કણની સરેરાશ ઝડપને કુલ પથલંબાઈ અને સમયગાળાના ગુણોત્તર વડે વ્યાખ્યાયિત કરવામાં આવે છે.] (a) અને (b) બંને માટે દર્શાવો કે બીજી રાશિ પ્રથમ રાશિ કરતાં મોટી કે તેના જેટલી જ છે. સમાનતાનું ચિહ્ન ક્યારે સાચું હશે ? [સરળતા માટે ગતિને એક પારિમાણિક ગતિ લો.]
View Solutionએક વ્યક્તિ સુરેખ માર્ગ `5 km h^(-1)`ની ઝડપે તેના ઘરેથી 2.5 km દૂર આવેલા માર્કેટમાં જાય છે. પરંતુ માર્કેટને બંધ જુએ છે, તે તરત જ `7.5 km h^(-1)`ની ઝડપે ઘરે પાછો ફરે છે તો, સરેરાશ વેગનું માન શોધો
View Solutionએક વ્યક્તિ સુરેખ માર્ગ `5 km h^(-1)`ની ઝડપે તેના ઘરેથી 2.5 km દૂર આવેલા માર્કેટમાં જાય છે. પરંતુ માર્કેટને બંધ જુએ છે, તે તરત જ `7.5 km h^(-1)`ની ઝડપે ઘરે પાછો ફરે છે તો,: સમયગાળા (i) 0 થી 30 min (ii) 0 થી 50 min (iii) 0 થી 40 min માટે વ્યક્તિની સરેરાશ ઝડપ કેટલી હશે ?
View Solutionતાત્ક્ષણિક ઝડપ હંમેશાં તાત્ક્ષણિક વેગના માન જેટલી હોય છે. શા માટે ?
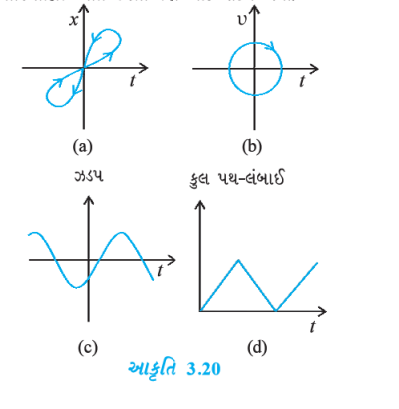
View Solutionઆકૃતિ 3.20માં દર્શાવેલ આલેખો (a) થી (d) ધ્યાનથી જુઓ અને કારણ સહિત જણાવો કે તે પૈકી કયો આલેખ એક પારિમાણિક ગતિ કરતાં કણ માટે શક્ય નથી.
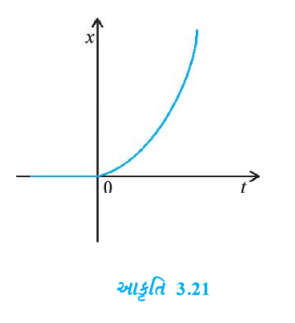
View Solutionઆકૃતિ 3.21માં કણની એક પારિમાણિક ગતિ માટે x - t આલેખ દર્શાવેલ છે. આલેખ પરથી એમ કહેવું સાચું છે કે, t < 0 માટે કણ સુરેખ માર્ગે અને t > 0 માટે પરવલય માર્ગે ગતિ કરે છે ? જો ના, તો આ આલેખ માટે યોગ્ય ભૌતિક સંદર્ભનો અભિપ્રાય આપો.
View Solutionકોઈ એક રાજમાર્ગ પર `30 km h^(-1)`ની ઝડપે દોડતી પોલીસવાનમાંથી, તેની જ દિશામાં `192 km h^(-1)` ઝડપે દોડી રહેલી ચોરની કાર પર ગોળી છોડવામાં આવે છે. જો બંદૂકની નળીમાંથી નીકળતી ગોળીની ઝડપ `150 m s^(-1)` હોય, તો ગોળી ચોરની કારને કઈ ઝડપે અથડાશે ?
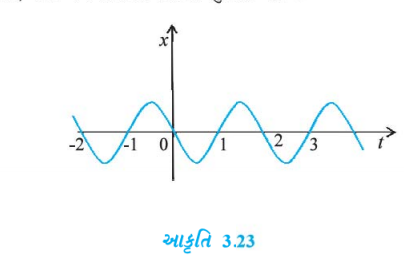
View Solutionઆકૃતિ 3.23માં એક પારિમાણિક સરળ આવર્તગતિ માટેનો x - t આલેખ દર્શાવેલ છે. (આ ગતિ વિશેનો વિગતવાર અભ્યાસ તમે પ્રકરણ 14માં કરશો.) સમય 1 = 0.3 s, 1.2 s, -1.2 s માટે કણનાં સ્થાન, વેગ અને પ્રવેગનાં ચિહ્નો શું હોઈ શકે ?
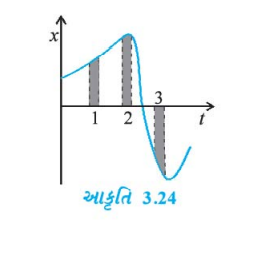
View Solutionઆકૃતિ 3.24માં એક પારિમાણિક ગતિ કરતાં કણ માટેનો x - t આલેખ દર્શાવેલ છે. જેમાં ત્રણ સમાન સમયગાળા દર્શાવેલ છે. કયા સમયગાળા માટે સરેરાશ ઝડપ સૌથી વધુ અને કયા માટે તે સૌથી ઓછી હશે ? દરેક સમયગાળાને અનુરૂપ સરેરાશ વેગનાં ચિહ્ન આપો.
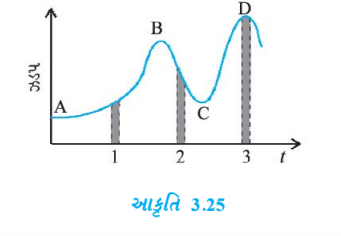
View Solutionઆકૃતિ 3.25માં અચળ દિશામાં ગતિ કરતાં કણ માટે ઝડપ-સમયનો આલેખ દર્શાવેલ છે. જેમાં ત્રણ સમાન સમયગાળા દર્શાવ્યા છે. કયા સમયગાળા માટે સરેરાશ પ્રવેગનું માન સૌથી વધુ હશે ? કયા સમયગાળા માટે સરેરાશ ઝડપ સૌથી વધુ હશે ? પદાર્થની અચળ ગતિની દિશાને ધન દિશા તરીકે પસંદ કરી, ત્રણેય સમયગાળાને અનુરૂપ છે v અને aનાં ચિહ્ન જણાવો. A, B, C અને D. બિંદુ પર પ્રવેગ શું હશે ?
View Solutionસ્થિર લિફ્ટ (ઉપરથી ખુલ્લી હોય તેવી)માં ઊભેલો એક બાળક `49 m s^(-1)` જેટલી મહત્તમ પ્રારંભિક ઝડપે એક દડાને ઊર્ધ્વદિશામાં ફેંકે છે. તો દડાને તેના હાથમાં પાછો આવવા માટે કેટલો સમય લાગશે ? જો લિફ્ટ `5 m s^(-1)` જેટલી નિયમિત ઝડપે ઉપર તરફ ગતિ કરવાની શરૂઆત કરે અને બાળક ફરીથી દડાને ઉપર તરફ તે જ મહત્તમ ઝડપે ફેંકે, તો કેટલા સમય પછી દડો બાળકના હાથમાં પરત આવશે ?
View Solutionઆકૃતિ 3.26માં દર્શાવ્યા મુજબ સમક્ષિતિજ લાંબો પટ્ટો `4 km h^(-1)` ઝડપે ગતિમાં છે. આ પટ્ટા પર એક બાળકનાં માતા-પિતા એકબીજાંથી 50 m દૂર બેઠાં છે અને બાળક પટ્ટાની સાપેક્ષે `9 km h^(-1)` ઝડપે પટ્ટા પર માતા-પિતાની વચ્ચે આગળ-પાછળ દોડે છે. પ્લેટફૉર્મ ઉપર સ્થિર ઊભેલ અવલોકનકાર માટે: પટ્ટાની ગતિની દિશામાં દોડતાં બાળકની ઝડપ શું હશે ?

View Solutionઆકૃતિ 3.26માં દર્શાવ્યા મુજબ સમક્ષિતિજ લાંબો પટ્ટો `4 km h^(-1)` ઝડપે ગતિમાં છે. આ પટ્ટા પર એક બાળકનાં માતા-પિતા એકબીજાંથી 50 m દૂર બેઠાં છે અને બાળક પટ્ટાની સાપેક્ષે `9 km h^(-1)` ઝડપે પટ્ટા પર માતા-પિતાની વચ્ચે આગળ-પાછળ દોડે છે. પ્લેટફૉર્મ ઉપર સ્થિર ઊભેલ અવલોકનકાર માટે : પટ્ટાની ગતિની વિરુદ્ધ દિશામાં દોડતા બાળકની ઝડપ શું હશે ?

View Solutionઆકૃતિ 3.29માં એક પરિમાણમાં ગતિ કરતાં કણ માટે વેગ-સમય આલેખ દર્શાવેલ છે.
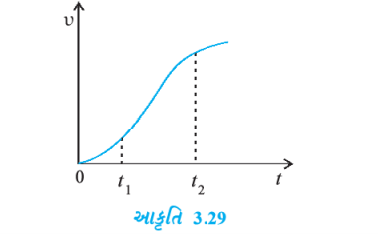 સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `x(t_2)=x(t_1)+v(t_1)(t_2-t_1)+(1//2) a (t_2-t_1)^2`
સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `x(t_2)=x(t_1)+v(t_1)(t_2-t_1)+(1//2) a (t_2-t_1)^2`
View Solutionઆકૃતિ 3.29માં એક પરિમાણમાં ગતિ કરતાં કણ માટે વેગ-સમય આલેખ દર્શાવેલ છે.
 સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `v(t_2)=v(t_1)+a(t_2-t_1)`
સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `v(t_2)=v(t_1)+a(t_2-t_1)`
View Solutionઆકૃતિ 3.29માં એક પરિમાણમાં ગતિ કરતાં કણ માટે વેગ-સમય આલેખ દર્શાવેલ છે.
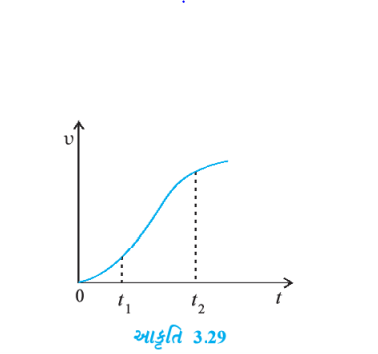 સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `v_("average")=[x(t_2)-x(t_1)]//(t_2-t_1)`
સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `v_("average")=[x(t_2)-x(t_1)]//(t_2-t_1)`
View Solutionઆકૃતિ 3.29માં એક પરિમાણમાં ગતિ કરતાં કણ માટે વેગ-સમય આલેખ દર્શાવેલ છે.
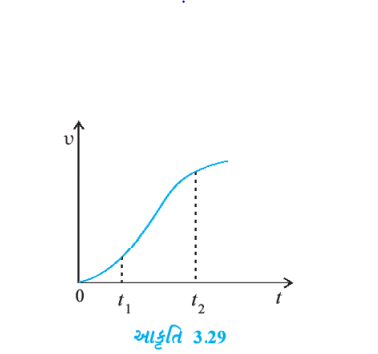 સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `a_("average")=[v(t_2)-v(t_1)]//(t_2-t_1)`
સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે : `a_("average")=[v(t_2)-v(t_1)]//(t_2-t_1)`
View Solutionઆકૃતિ 3.29માં એક પરિમાણમાં ગતિ કરતાં કણ માટે વેગ-સમય આલેખ દર્શાવેલ છે.
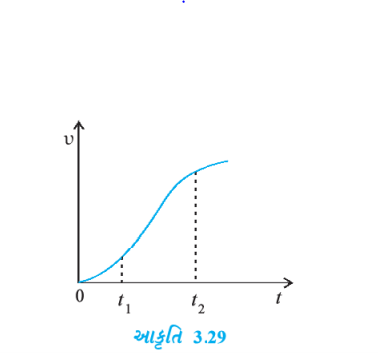 સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે :
(a) `x(t_2)=x(t_1)+v(t_2-t_1)+(1//2)a(t_2-t_1)^2`
(b) `x(t_2)-x(t_1)` = t-અક્ષ અને ત્રુટક રેખા વડે v - t વક્ર નીચે ઘેરાતું ક્ષેત્રફળ.
સમયગાળા `t_1` થી `t_2` માટે નીચેમાંથી કયાં સમીકરણો કણની ગતિને વર્ણવે છે :
(a) `x(t_2)=x(t_1)+v(t_2-t_1)+(1//2)a(t_2-t_1)^2`
(b) `x(t_2)-x(t_1)` = t-અક્ષ અને ત્રુટક રેખા વડે v - t વક્ર નીચે ઘેરાતું ક્ષેત્રફળ.
View Solution
Exercise questions and complete solutions for chapter સુરેખપથ પર ગતિ of NCERT Physics(Gujarati) of Class 11