Complete Solutions to EXAMPLE of chapter COMBINATORICS AND MATHEMATICAL INDUCTION of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | COMBINATORICS AND MATHEMATICAL INDUCTION |
| TAMILNADU GOVT | EXAMPLE |
| Number Of Questions | 90 |
| Academic Year | 2023-24 |
Suppose one girl or one boy has to be selected for a competition from a class comprising 17 boys and 29 girls. In how many different ways can this selection he made?
View SolutionConsider the 3 cities Chennai, Trichy and Triunelveli. In order to reach Tirunelveli from Chennai, one has to pass through Trichy. There are 2 roads connecting Chennai with Trichy and ther are 3 roads connecting with Tirunelveli. What are the total number of ways of travelling from Chennai to Tirunelveli.?
View SolutionA school library has 75 books on Mathematics, 35 books on Physics. A student can chose only book. In how many ways a student can chose a book on Mathematics or physics?
View SolutionIf an electricity consumer has the consumer number say 238:110:29, then describe linking and count the number of house connections upto the 29 the consumer connection linked to the larger capacity tranformer number 238 subject to the condition that each smaller capacity transformer can have a maximal consumer link of say 100.
View SolutionA person wants to buy a car. There are two brands of car available in the market and each brand has 3 variant models and each model comes in five different colours as in figure 4.3 in how many ways she can choose a car to buy?
View SolutionA woman wants to select one silk saree and sungudi saree from a textile shop located at Kancheepuram. In that shop, there are 20 different varieties of silk sarees and 8 different varieties of sungudi sarees. In how many ways she can select her sarres?
View SolutionIn a village out of the total number of people, 80 percentage of the people own coconut groves and 65 percent of the people own Pady fields. What is the minimum percentage of people own both?
View SolutionFind the number of strings of length 4, which can be formed using the letters of the word BIRD, without repetition of the letters.
View SolutionHow many strings of length 5 can be formed out of the letters of the word PRIME taking all the letters at a time without repetition.
View SolutionHow many strings of length 6 can be formed using letters of the world FLOWER if
(i) either starts with F or ends with R?
(ii) neither starts with F nor ends with R?
View SolutionHow many licence plates may be made using either two distinct letters followed by four digits or two digits followed by 4 distinct letters where all digits and letters are distinct?
View SolutionCount the number of positive integers greater than 7000 and less than 8000 which are divisible by 5, provided that no digits are repeated.
View SolutionHow many 4 -digit even numbers can be formed using the digits 0,1,2,3 and 4, if repetition of digits are not permitted?
View SolutionFind the total number of outcomes when 5 coins are tossed once.
View SolutionIn how many ways (i) 5 different balls be distributed among 3 boxes? (ii) 3 different balls be distributed among 5 boxes?
View SolutionThere are 10 bulbs in a room. Each one of them can be operated independently. Find the number of ways in which the room can be illuminated.
View SolutionFind the value of
`5!`
View SolutionFind the value of
`6!-5!`
View SolutionFind the value of
`(8!)/(5!xx2!)`
View SolutionSimplify: `(7!)/(2!)`
View SolutionEvaluate `(n!)/(r!(n-r)!)` when
n=7,r=5
View SolutionEvaluate `(n!)/(r!(n-r)!)` when
n=50,r=47
View SolutionEvaluate `(n!)/(r!(n-r)!)` when
For any n with r=3
View SolutionLet N denote the number of days. If the value of N! is equal to the total number of hours in N days then find the value of N?
View SolutionIf `(6!)/(n!)=6` then find the value of n
View SolutionIf `n!+(n-1)!=30` then find the value of n
View SolutionWhat is the unit digit of the sum `2!+3!+4!+……….+22!`?
View SolutionIf `1/(7!)+1/(8!)=A/(9!)` then fin the value of A.
View SolutionProve that `((2n)!)/(n!)=2^(n)(1.3.5…..(2n-1))`
View SolutionEvaluate:
`""^(4)P_(4)`
View SolutionEvaluate:
`""^(5)P_(3)`
View SolutionEvaluate:
`""^(8)P_(4)`
View SolutionEvaluate:
`""^(6)P_(5)`
View SolutionIf `""^((n+2))P_(r)=42xx""^(n)P_(2)`, find n
View SolutionIf `""^(10)P_(r)=""^(7)P_(r+2)` find r
View SolutionHow many letter strings together can be formed with the letters of the word VOWELS so that
the strings begin with E
View SolutionHow many letter strings together can be formed with the letters of the word VOWELS so that
the strings begin with E and end with W
View SolutionA number of four different digits is formed with the use of digits 1,2,3,4, and 5 in all possible ways. Find the following
How many such numbers can be formed?
View SolutionA number of four different digits is formed with the use of digits 1,2,3,4, and 5 in all possible ways. Find the following
How many of these are even?
View SolutionA number of four different digits is formed with the use of digits 1,2,3,4, and 5 in all possible ways. Find the following
How many of these are exactly divisible by 4?
View SolutionHow many different strings can be formed together using the letters of the word EQUATION so that
the vowels always come together?
View SolutionHow many different strings can be formed together using the letters of the word EQUATION so that
the vowels never come together?
View SolutionThere are 15 candidates for an examination 7 candidats are appearing for mathematics examination while the remaining 8 are appearing for different subjects. In how many ways can they be seated in a row so that no two mathematics candidates are together?
View SolutionIn how many ways 5 boys and 4 girls can be seated in a row so that no two girls are together.
View Solution4 boys and 4 girls form a line with the boys and girls alternating. Find the number of ways of making this line.
View SolutionA has 8 seats. If has two seats in the front with two rows of three seats behind. The van belongs to a family consisting of seven members, `F,M,S_(1),S_(2),S_(3), D_(1),D_(2)`. How many ways can the family sit in the van if
There are no restriction?
View SolutionA has 8 seats. If has two seats in the front with two rows of three seats behind. The van belongs to a family consisting of seven members, `F,M,S_(1),S_(2),S_(3), D_(1),D_(2)`. How many ways can the family sit in the van if
Either F or M drives the van?
View SolutionA has 8 seats. If has two seats in the front with two rows of three seats behind. The van belongs to a family consisting of seven members, `F,M,S_(1),S_(2),S_(3), D_(1),D_(2)`. How many ways can the family sit in the van if
`D_(1),D_(2)` sits next to a window and F is driving?
View SolutionIf the letters of the word TABLE are permuted in all possible ways and the words thus formed are arranged in the dictionary order (alphabetical order), find the ranks of the words
TABLE
View SolutionIf the letters of the word TABLE are permuted in all possible ways and the words thus formed are arranged in the dictionary order (alphabetical order), find the ranks of the words
BLEAT
View SolutionFind the number of ways of arranging the letters of the word BANANA.
View SolutionFind the number of ways of arranging the letters of the word RAMANUJAN so that the relative positions of vowels and consonants are not changed.
View SolutionThree twins pose for a photograph standing in a line. How many arrangements are there (i) when there are no restrictions.
View SolutionThree twins pose for a photograph standing in a line. How many arrangements are there
when each person is standing next to his or her twin?
View SolutionHow many numbers can be formed using the digits 1,2,3,4,2,1 such that even digits occupies even place?
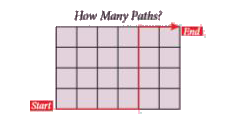
View SolutionHow many paths are there from start to end on a `6xx4` grid as shown in the picture?
View SolutionIf the different permutations of all letters of the word BHAKARA are listed as in a disctionary how many strings are there in this list before the first word starting with B?
View SolutionIf the letters of the word IITJEE are permuted in all possible ways and the strings thus formed are arranged in the lexicographic order, find the rank of the word IITJEE.
View SolutionFind the sum of all 4-digit numbers that can be formed using thedigit 1,2,4,6,8.
View SolutionEvaluate the following
`""^(10)C_(3)`
View SolutionEvaluate the following
`""^(15)C_(13)`
View SolutionEvaluate the following
`""^(100)C_(99)`
View SolutionEvaluate the following
`""^(50)C_(50)`
View SolutionFind the values of `""^(5)C_(2)` and `""^(7)C_(2)` using the property 5
View SolutionIf `""^(n)C_(4)=495` What is n?
View SolutionIf `""^(n)P_(r)=11880` and `""^(n)C_(4)=495` Find n and r
View SolutionProve that `""^(24)C_(4)+sum_(r=0)^(4)""^((28-r))C_(3)=""^(29)C_(4)`
View SolutionProve that `""^(10)C_(2)+2xx""^(10)C_(3)+""^(10)C_(4)=""^(12)C_(4)`
View SolutionIf `""^((n+2))C_(7):""^((n-1))P_(4)=13:24` find n
View SolutionA salad at a certain restaurant consists of 4 of the following fruits. Apple, banana, guava, pomegranate, grapes, papaya and pineapple. Find the total possible number of fruit salads.
View SolutionA matematics club has 15 memebts.In that 8 are girls 6 of the members are to be selected for a competition and half of them should be girls. How many ways of these selections are possible?
View SolutionIn rating 20 brands of cars, a car magazine picks a first, second, third, fourth and fifth bestbrand and then 7 more as acceptable.In how many ways can it be done?
View SolutionFrom a class of 25 students, 10 students are to be chosen for an excursion party. There are 4 students who decise that either all of them will join ornone of them will join. In how many ways can the excursion party be chosen?
View SolutionA box of one dozen apple contais a rotten apple.If we are choosing 3 apples simultaneously, in how many ways one can get only good apples.
View SolutionAn exam paper contains 8 question 4 in part A and 4 in part B. Examiners are required to answer 5 questions. In how many ways can this be done if
There are no restrictions of choosing a number of questions in either parts.
View SolutionAn exam paper contains 8 question 4 in part A and 4 in part B. Examiners are required to answer 5 questions. In how many ways can this be done if
At least two questions from Part A must be answered.
View SolutionOut of 7 consonants and 4 vowels, how many strings of 3 consonants and 2 vowels can be formed?
View SolutionFind the number of strings of 5 letters that can be formed with the letters of the word PROPOSITION
View SolutionIf a set of m parallel lines intersect another set of n parallel lines (not parallel to the lines in the first set), then the find the number of parallelograms formed in this lattice structure.
View SolutionHow many diagonals are there in a polygon with n sides?
View SolutionBy the principle of mathematical induction, prove that for all integers `nge1`,
`1+2+3+…………..+n=(n(n+1))/2`
View SolutionProve that the sum of first n positive odd numbers is `n^(2)`.
View SolutionBy the principle of mathematical induction, prove that for all integers `n ge 1`
`1^(2)+2^(2)+3^(2)+……….+n^(2)=(n(n+1)(2n+1))/6`
View SolutionUsing the Mathematical induction, show that for any natural number n,
`1/1.2+1/2.3+1/3.4+……….+1/(n(n+1))=n/(n+1)`
View SolutionProve that the for any natural number `n,a^(n)-b^(n)` is divisible by a-b where `a gt b`
View SolutionProve that `3^(2n+2)-8n-9` is divisible by 8 for all `n ge 1`
View SolutionUsing the Mathematical induction show that for any integer
`n ge 2, 3n^(2)gt(n+1)^(2)`
View SolutionUsing the Mathematical induction, show that for any integer
`n ge 2, 3^(n)gt n^(2)`
View SolutionBy the principle of mathematical induction prove that for `n in NN`
`cos alpha+cos (alpha+beta)+cos (alpha+2beta)+………+cos (alpha+(n-1)beta)=cos(alpha+((n-1)beta)/2)xx(sin((n beta)/2))/(sin((beta)/2))`
View SolutionUsing the Mathematical induction, show that for any natual number n, with the assumption `i^(2)=-1`
`(r(cos theta +I sin theta))^(n)=r^(n)(cos n theta+I sin n theta)`
View Solution
EXAMPLE questions and complete solutions for chapter COMBINATORICS AND MATHEMATICAL INDUCTION of FULL MARKS MATHEMATICS(TAMIL) of Class 11