Complete Solutions to EXERCISES of chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SYSTEMS OF PARTICLES AND ROTATIONAL MOTION |
| NCERT TAMIL | EXERCISES |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
Given the location of the centre of mass of a (i) sphere, (ii) cylinder, (iii) ring, and (iv) cube, each of uniform mass density. Does the centre of mass of a body necessarily lie on the body ?
View SolutionIn the `HCI` molecule, the separation between the nuclei of the two atoms is about `1.27Å (1Å = 10^(-10)m)`. Find the approximate location of the c.m of the molecule, given that a chlorine atom is about `35.5` times as massive as a hydrogen atom and nearly all the mass of an atom is concentrated in its nucleus ?
View SolutionA child is standing at one end of a long trolley moving with a speed v on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed u, the centre of mass of the system (trolley + child) will move with a speed :
View SolutionShow that the area of the triangle contained between the vectors a and b is one half of the magnitude of `a × b`.
View SolutionShow that `veca.(vecbxxvec c)` is equal in magnitude to the volume of the parallelpiped formed by the vectors `veca,vecb and vec c`
View SolutionFind the components along the `x,y,z` axes of the angular momentum `overset rarr(L)` of a particle, whose position vector is `overset rarr(r )` with components `x,y,z` and momentum is `overset rarr(p)` with components `p_(x), p_(y) and p_(z)`. Show that if the particle moves only in the `x-y` plane, the angular momentum has only a z-component.
View SolutionTwo particles each of mass `m` and speed `v`, travel in opposite direction along parallel lines separated by a distance d. Show that the vector angular momentum of this system of particles is the same about any point taken as origin.
View SolutionFind the value of x in the following figures.
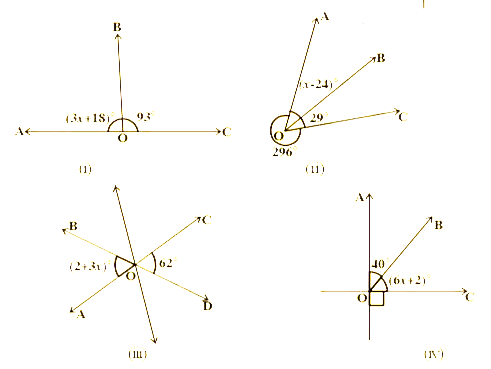
View SolutionA car weighs `1800 kg`. The distance between its front and back axles is `1.8 m`. Its centre of gravity is `1.05 m` behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
View Solution(a) Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be `2 MR^(2)//5, where M` is the mass of the sphere and `R` is the radius of the sphere.
(b) Given the moment of inertia of a disc of mass `M` and radius `R` about any of its diameters to be `(1)/(4)MR^(2)`, find the moment of inertia about an axis normal to the disc passing through a point on its edge.
View SolutionTorques of equal magnitude are applied to hollow cylinder and a solid sphere, both having the same mass and same radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. which of the two will acquire a greater angular speed after a given time ?
View SolutionA solid cylinder of mass `20 kg` rotates about its axis with angular speed `100 s^(-1)`. The radius of the cylinder is `0.25 m`. What is the kinetic energy associated with the rotation of the cylinder ? What is the magnitude of angular momentum of the cylinder about its axis ?
View SolutionA child stands at the centre of a turn table with his two arms outstretched. The turn table is set rotating with an angular speed of `40` rpm. How much is the angular speed of the child, if he folds his hands back reducing the moment of inertia to `(2//5)` time the initial value ? Assume that the turn table rotates without friction.
(b) Show that the child's new `K.E.` of rotation is more than the initial `K.E.` of rotation. How do you account for this increase in `K.E.` ?
View SolutionA rope of negligible mass is wound around a hollow cylinder of mass `3 kg` and radius `40 cm`. What is the angular acceleration of the cylinder, if the rope is pulled with a force of `30 N` ? What is the linear acceleration of the rope ? Assume that there is no slipping.
View SolutionTo maintain a rotor at a uniform angular speed of 100 `rads^(-1)` an engine needs to transmit a torque of 200 Nm. What is the power required by engine ? Assume 100 % efficiency of engine.
View SolutionFrom a uniform disc of radius `R`, a circular section of radius `R//2` is cut out. The centre of the hole is at `R//2` from the centre of the original disc. Locate the centre of mass of the resulting flat body.
View SolutionA metre stick is balanced on a knife edge at its centre. When two coins, each of mass `5 g` are put one on one of the other at the `12 cm` mark, the stick is found to balanced at `45 cm`. The mass of the metre stick is.
View SolutionA solid wooden sphere rolls down two different inclined planes of the same height but of different inclinations. (a) Will it reach the bottom with same speed in each case ?
(b) Will it take longer to roll down one inclined plane than other ? Explain.
View SolutionA hoop of radius 2m, weight 100 kg. It rolls along horizontal floor so that its center of mass has a speed of `20 cm/s`. How much work has to be done to stop it?
View SolutionThe oxygen molecule has a mass of `5.30 xx 10^(-26) kg` and a moment of inertia of `1.94 xx 10^(-46) kg m^(2)` about an axis through its centre perpendicular to the line joining the two atoms. Suppose the mean speed of such a molecule in a gas is `500 m//s` and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
View SolutionA sphere rolls up an inclined plane whose inclination is `30^(@)`. At the bottom of the inclined plane, the center of mass of the sphere has a translational speed of `5ms^(-1)` (a) How far does the sphere travel up the plane? (b) How long does it take to return to the bottom?
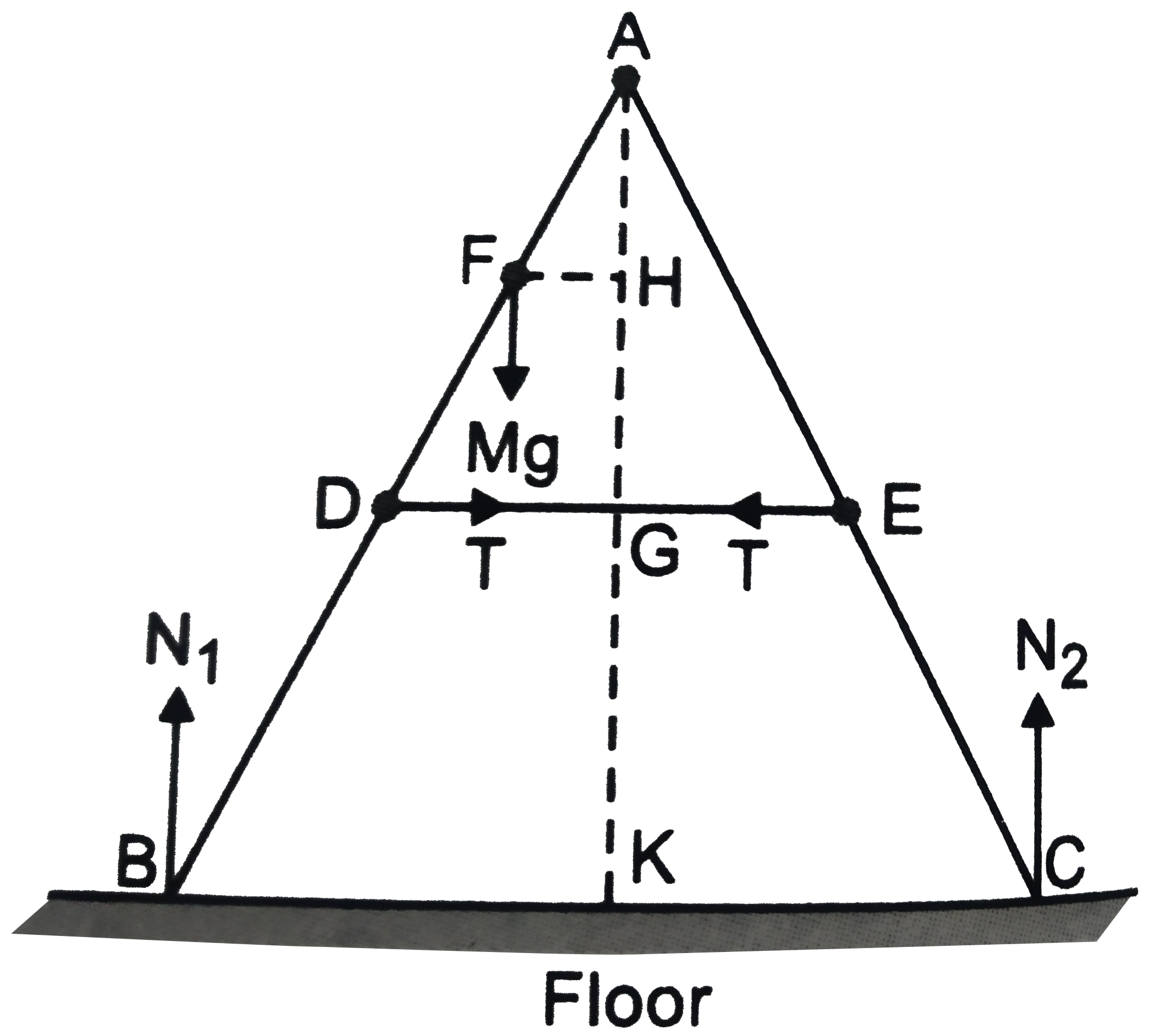
View SolutionAs shown in Fig. the two sides of a step ladder `BA` and `CA` are `1.6 m` long and hinged at `A`. A rope `DE, 0.5 m` is tied half way up. A weight `40 kg` is suspended from a point `F, 1.2 m` from B along the ladder` BA`. Assuming the floor to be fricionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take `g = 9.8 m//s^(2))`
(Hint. Consider the eqilibrium of each side of the ladder separately.)
View SolutionA man stands on a rotating platform, with his arms stretched horizontal holding a `5 kg` weight in each hand. The angular speed of the platform is `30` revolutions per minute. The man then brings his arms close to his body with the distance of each weight from the axis changing from `90 cm` to `20 cm`. moment of inertia of the man together with the platform may be taken to be constant and equal t `7.6 kg m^(2)`. (a) What is the his new angular speed ? (Neglect friction.)
(b) Is kinetic energy conserved in the process ? If not, from where does the change come about ?
View SolutionA bullet of mass `10 g` and speed `500 m//s` is fired into a door and gets embedded exactly at the centre of the door. The door is `1.0 m` wide and weight `12 kg`. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint. The moment of inertia of the door about the vertical axis at one end is `ML^(2)//3)`
View SolutionTwo discs of moments of inertia `I_(1) and I_(2)` about their respective axes (normal to the disc and passing through the centre), and rotating with angular speed `omega_(1) and omega_(2)` are brought into contact face to face with their axes of rotation coincident . What is the angular speed of the two-disc system ?
View Solution(a) Prove the theorem of perpendicular axes.
(Hint : Square of the distance of a point (x, y) in the x-y plane from an axis through the origin and perpendicular to the plane is `(x^(2)+y^(2))`.
(b) Prove the theorem of parallel axes.
(Hint : If the centre of mass of a system of n particles is chosen to be the origin `summ_(i)r_(i)=0`).
View SolutionProve the result that the velocity `v` of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclined plane of a height h is given by `v^(2) = (2gh)/((1 + k^(2)//R^(2))` using dynamical consideration (i.e. by consideration of forces and torque). Note k is the radius of gyration of the body about its symmetry axis, and `R` is the radius of the body. The body starts from rest at the top of the plane.
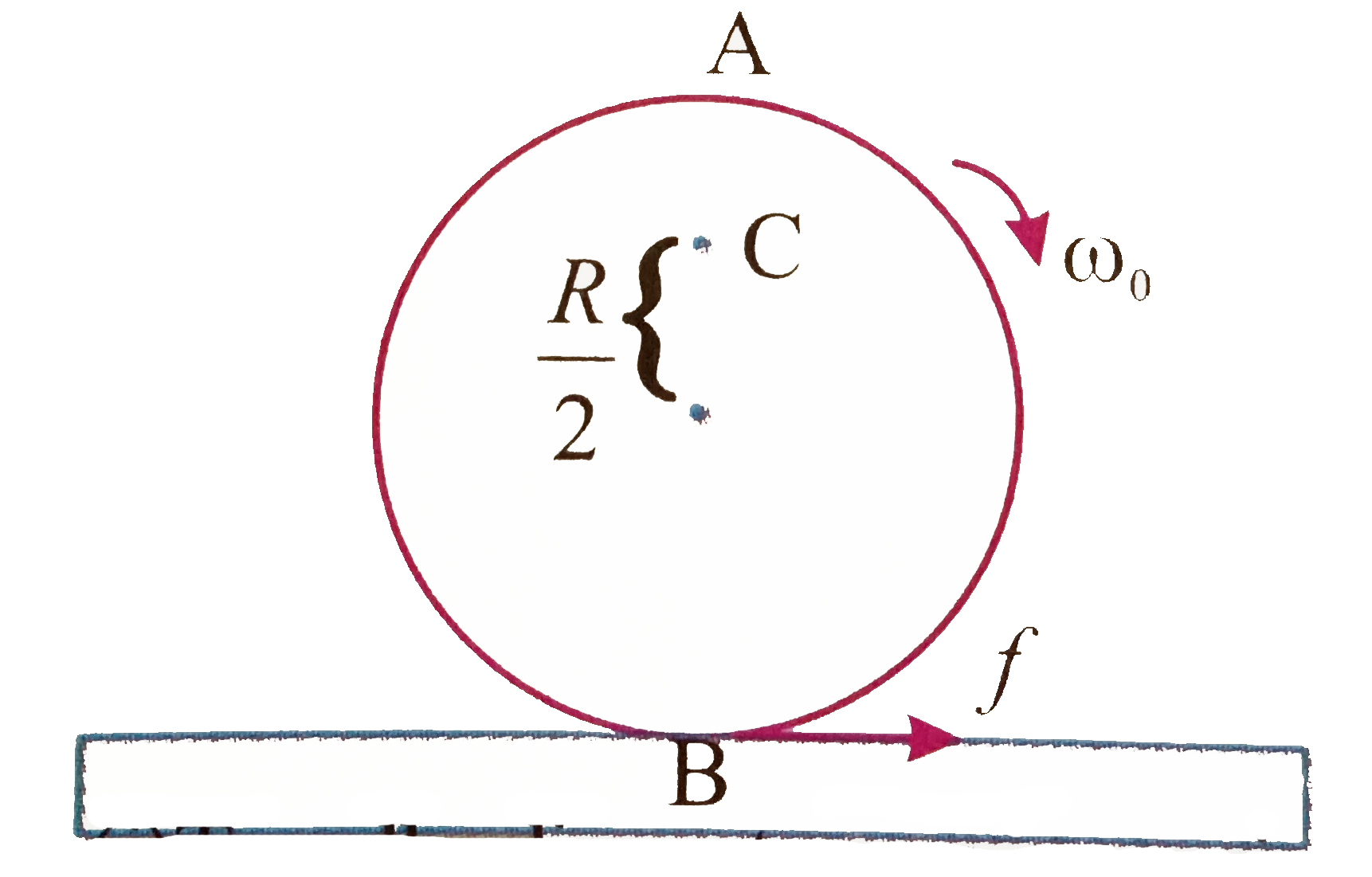
View SolutionA disc rotating about its axis with angular speed `ω_(o)` is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A, B and C on the disc shown in Fig. 7.41? Will the disc roll in the direction indicated ?
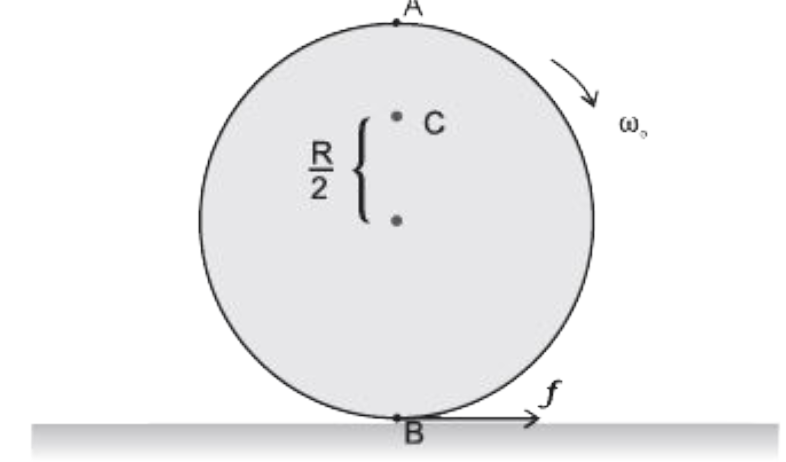
View Solution(i) Explain why friction is necessary to make the disc to roll in the direction indicated. (ii) Give the direction of frictional force at `B`, and the sense of frictional torque, before perfect rolling begins. (iii) What is the force of friction after perfect rolling begins?
View SolutionA solid disc and a ring, both of radius `10 cm` are placed on a horizontal table simultaneously, with initial angular speed equal to `10 pi rad//s`. Which of the two will start to roll earlier ? The coefficient of kinetic friction is `mu_(k) = 0.2`.
View SolutionA cylinder of mass `10 kg` and radius `15 cm` is rolling perfectly on a plane of inclination `30^(@)`. The coefficient of static friction is `mu_(s) = 0.25`.
(a) How much is the force of friction acting on the cylinder ?
(b) What is the work done against friction during rolling ?
(c ) If the inclination `theta` of plane is increased, at what value of `theta` does the cylinder begin to skid and not roll perfectly ?
View SolutionSeparation of Motion of a system of particles into motion of the centre of mass and motion about the centre of mass :
(a) Show `p=p_(i)'+m_(i)V`
where pi is the momentum of the ith particle (of mass `m_(i)`) and `p'_(i)=m_(i)v'_(i)`. Note `v'_(i)` is the velocity of the ith particle relative to the centre of mass.
Also, prove using the definition of the centre of mass `sump'_(i)=O`
(b) Show `K=K'+1//2MV^(2)`
where K is the total kinetic energy of the system of particles, K′ is the total kinetic energy of the system when the particle velocities are taken with respect to the centre of mass and `MV^(2)//2` is the kinetic energy of the translation of the system as a whole (i.e. of the centre of mass motion of the system). The result has been used in Sec. 7.14.
(c ) Show `L=L'+RxxMV`
where `L'=sumr'_(i)xxp'_(i)` is the angular momentum of the system about the centre of mass with velocities taken relative to the centre of mass. Remember – `r'_(i)=r_(i)-R` , rest of the notation is the standard notation used in the chapter. Note ′ L and `MR × V` can be said to be angular momenta, respectively, about and of the centre of mass of the system of particles.
(d) Show `(dL')/(dt)=sumr'_(i)xx(dp')/(dt)`
Further, show that
`(dL')/(dt)=tau'_(ext)`
where `tau'_(ext)` is the sum of all external torques acting on the system about the centre of mass.
View Solution
EXERCISES questions and complete solutions for chapter SYSTEMS OF PARTICLES AND ROTATIONAL MOTION of FULL MARKS PHYSICS(TAMIL) of Class 11