Complete Solutions to EXAMPLES of chapter WORK, ENERGY AND POWER of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WORK, ENERGY AND POWER |
| NCERT TELUGU | EXAMPLES |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
Find the angle between force `F= (3hati+4hatj-5hatk)` unit and displacement `d= (5hati+4hatj+3hatk)` unit. Also find the projection of F and d.
View SolutionIt is well known that a raindrop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop but is otherwise undetermined. Consider a drop of mass `1.00g` falling from a height `1.00km`. It hits the ground with a speed of `50.0 ms^(-1)`.
What is the work done by the gravitational force?
View SolutionIt is well known that a raindrop falls under the influence of the downward gravitational force and the opposing resistive force. The latter is known to be proportional to the speed of the drop but is otherwise undetermined. Consider a drop of mass `1.00g` falling from a height `1.00km`. It hits the ground with a speed of `50.0 ms^(-1)`.
What is the work done by the unknown resistive force?
View SolutionAcyclist comes to a skidding stop in 10m. During this process, the forceon the cycle due to the road is 200 N and is directy opposed to the motion.
How much work does the road do on the cycle?
View SolutionAcyclist comes to a skidding stop in 10m. During this process, the forceon the cycle due to the road is 200 N and is directy opposed to the motion.
How much work does the cycle do on the road?
View SolutionIn a ballistics demonstration a police officer fires a bullet of mass `50.0 g` with speed `200 ms^(-1)` (see Table 6.2) on soft plywood of thickness 2.00 cm. The kinetic energy. What is the emergent speed of the bullet?
View SolutionA woman pushes a trunk on a railway platform which has a rough surface. She applies a force of 100 N over a distance of 10m. Thereafter, she gets progressively tired and her applied force reduces linearly with distance to 50 N. The total distance through which the trunk has been moved is 20m. Plot the force applied by the woman and the frictional force, which is 50 N versus displacement. Calculate the work done by the two forces over 20 m.
View SolutionA block of mass `m= 1 kg`, moving on a horizontal surface with speed `v_(t)= 2 ms^(-1)` enters a rough patch ranging from `x= 0.10m" to "x= 2.01m`. The retarding force `F_(r )` on the block in this range is inversely proportional to x over this range,
`F_(r )= (-k)/(x)" for "0.1 lt x lt 2.01m = 0 " for "x lt 0.1m" and "x gt 2.01m`
where `k= 0.5 J`. What is the final kinetic energy and speed `v_(f)` of the block as it crosses this patch?
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(o)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
`v_(o)`
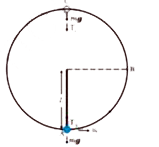
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(o)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
The speeds at points B and C.
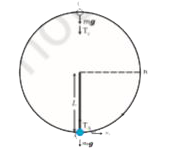
View SolutionA bob of mass m is suspended by a light string of length L. It is imparted a horizontal velocity `v_(o)` at the lowest point A such that it completes a semi-circular trajectory in the vertical plane with the string becoming slack only on reaching the topmost point, C. This is shown in Fig. 6.6. Obtain an expression for
The ratio of the kinetic energies `(K_(B)"/"K_(C ))` at B and C. Comment on the nature of the trajectory of the bob after it reaches the point C.
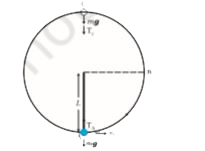
View SolutionTo simulate car accidents, auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000 kg moving with a speed `18.0 km/h` on a smooth road and colliding with a horizontally mounted spring of spring constant `6.25xx10^(3) Nm^(-1)`. What is the maximum compression of the spring?
View SolutionConsider Example 6.8 taking the coefficient of friction, u, to be `0.5` and calculate the maximum compression of the spring.
View SolutionExamine Tables 6.1-6.3 and express
The energy required to break on bond in DNA in eV.
View SolutionExamine Tables 6.1-6.3 and express
The kinetic energy of an air molecule `(10^(-21)J)` in eV.
View SolutionExamine Tables 6.1-6.3 and express
The daily intake of human adult in kilocalories.
View SolutionAn elevator can carry a maximum load of 1800 kg (elevator + passengers) is moving up with a constant speed of `2ms^(-1)`. The frictional force opposing the motion is 4000 N. Determine the minimum power delivered by the motor to the elevator in watts as well as in horse power.
View SolutionIn a nuclear reactor a neutron of high speed (typically `10^(7) ms^(-1)`) must be slowed to `10^(3) ms^(-1)` so that it can have a high probability of interacting with isotope `{:(235),(92):}U` and causing it to fission. Show that a neutron can lose most of its kinetic energy in an elastic collision with a light nuclet like deuterium or carbon which has a mass of only a few times the neutron mass. The material making up the light nuclet, usually heavy water `(D_(2)O)` or graphite, is called a moderator.
View SolutionConsider the collision depicted in Fig. 6.10. to be between two billiard balls with equal masses `m_(1)= m_(2)`. The first ball is called the cue while the second ball is called the target. The billiard player wants to 'sink' the target ball in a corner pocket, which is at an angle `theta_(2)= 37^(@)`. Assume that the collision is elastic and that friction and rotational motion are not important. Obtain `theta_(1)`.
View Solution
EXAMPLES questions and complete solutions for chapter WORK, ENERGY AND POWER of NCERT PHYSICS(TELUGU) of Class 11