Complete Solutions to All Questions of chapter FIRST LAW OF THERMODYNAMICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FIRST LAW OF THERMODYNAMICS |
| NN GHOSH | All Questions |
| Number Of Questions | 39 |
| Academic Year | 2023-24 |
A waterfall whose vertical height is `100m` discharges water into a pool below the fall. Calculate the rise in temperature of water assuming that all the heat remains in the water. (Specific heat capacity of water `=4200J kg^(-1)K^(-1)`)
View SolutionA bullet of mass `20xx10^(-3)kg` enters into a fixed block of wood with a velocity of `100ms^(-1)` and is brought to rest in the wood. Calclate the rise in temperature of te bullet if two -third of the heat produced is absorbed by the bullet. (Specific heat capacity of lead `=32calkg^(-1)K^-1)` and `J=4.2J//"callorie"`)
View SolutionHow much work in joule is done in producing heat necessary to convert 10g of ice at `-5^(@)C` into steam at `100^(@)C`? Given specificheat of ice `=0.5 cal g^(-1).^(@)C^(-1)`, latent heat of steam `= 540 cal g^(-1)`.
View SolutionA meteorite of mass `10^(4)kg` enters into atmosphere with a velocity of `10^(3) ms^(-1)`. How many calories of theat is produced when it is stopped due to frictioin with atmospheric ariL? `(J=4.2` joules per calorie)
View SolutionIn the determination of `J` buy Joule's experiment, the weights of mass `1kg` each were allowed to fall through `1m`. When the fell 80 times the temperature of the water in the calorimeter increased by `3^(@)C`. Calculate `J` if the time taken for each fall was 1 second and the water equivalent of the calorimeter and its contents `100xx10^(-3)` kg. Sp. heat capacity of water `=1000 cal kg^(-1)K^(-1)`.
View SolutionAn immersion type electric heater of `250` watts is immersed in `5 kg ` of water contained in a bucket. In how much time will the temperature water rise by `10^(@)C`? Sp heat capacity of water `1000cal kg^(-1)K^(-1)` and `J=4.1J cal ^(-1)`. Neglect heat capacity of bucket.
View SolutionA cyclic process for an ideal monatomic gas `(C_(v)=12.5Jmol^(-1)K^(-1)`) is represented in the figure. The temperature at 1, 2 and 3 are `300K, 600K` and `455K`, respectively. Compute the values of `DeltaQ, DeltaU` and `DeltaW` for each of the process. The process from 2 to 3 is adiabatic.
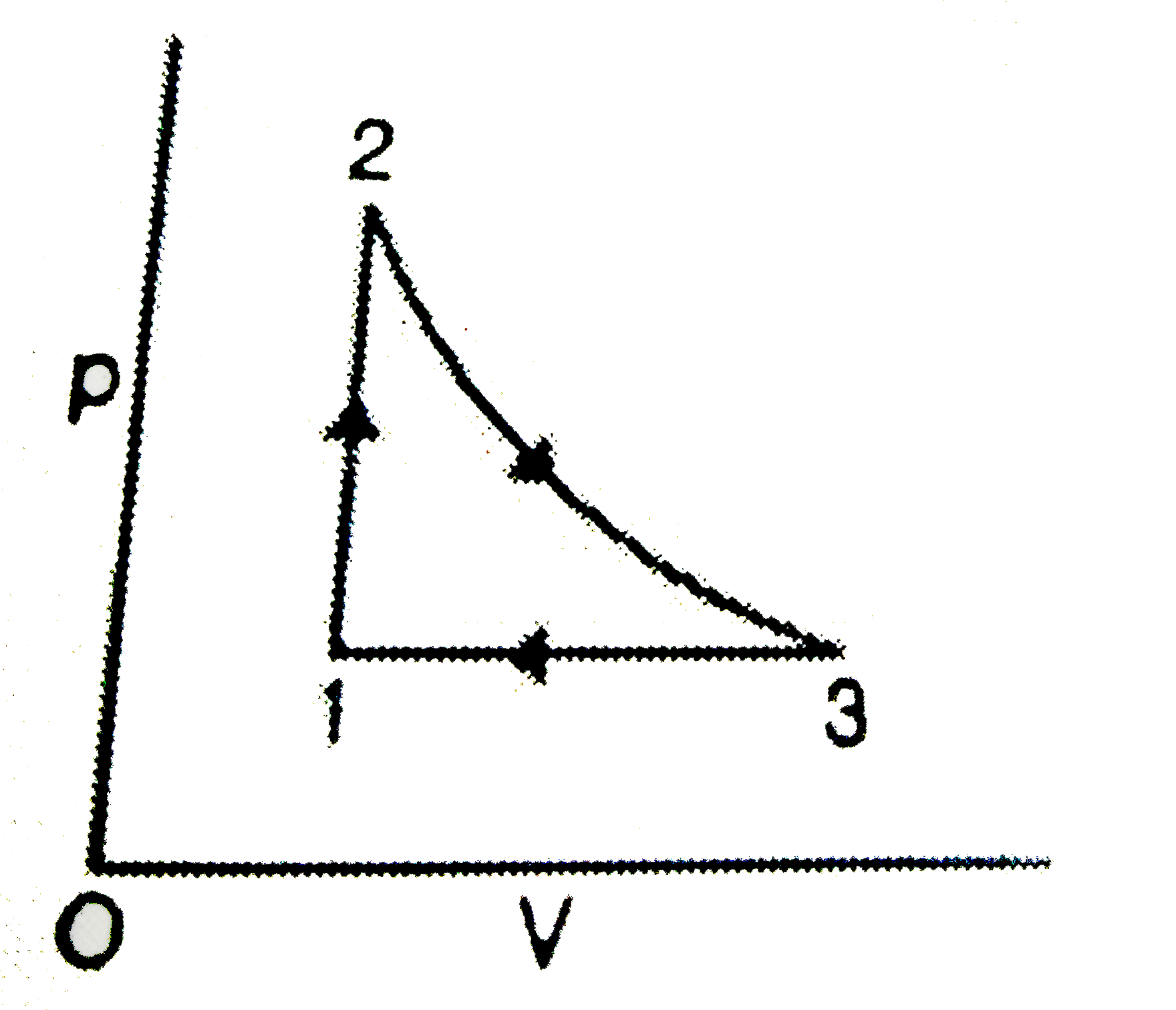
View SolutionFind the internal energy of air in a room of volume `40m^(3)` at 1 standard atmospheric pressure.
View SolutionA saturated water vaporu `(M=18)` is contained in a vessel fitted with a piston at a temeprature `t=100^(@)C`. As a result of slow introduction of the piston a small fractioin of the vapour `Deltam=1g` gets condensed. What amount of work is done over the gas?
View SolutionWater of mass `m=1kg` and `M` (mol mass) `=18` turns completely into saturated vapour at standard atmospheric pressure. Assuming the saturated vapour to be an ideal gas find increment of internal energy of the system. Specific latent heat of steam is `L=2550kJ//kg`
View SolutionThe height of the Niagara Falls is `50m`.Calculate the difference between the temperature of water at the top and the botom of the falls. (Specific heat capcity of water `=1000` calories per kg and `J=4.2` joules per calorie).
View SolutionIf a slice of bread can supply 100 kilocalorie of heat to a man, how many metres can a man weighting `60kg` climb by using this energy? (Efficiency of working of the human body `=30% J =4.2` joules per calorie and `g=9.8ms^(-2)`)
View SolutionHow much work is needed to convert `5g` of ice at `-3^(@)C` to steam at `100^(@)C`? (Sp. Heat capacity of ice `=500 cal kg^(-1)K^(-1)` sp. Latent heat of fusion of ice `=80xx10^(3) cal kg^(-1)` sp. Latent heat of vaporization of water `=536xx10^(3)calkg^(-1)`, and `J=4.2` joules per calorie)
View SolutionA tube of length `2m` containing a little mercury and closed at both ends is rapidly inverted 50 times. What is the maximum rise in temperature expected? (Specific heat capacity of mercury `=30calkg^(-1) K^(-1)` and `J=4.2` joules//cal.)
View SolutionHow much work is done agaist uniform pressure when `1g` of water at `100^(@)C` is converted into steam? Express your result in calories `(J=4.2` joules per calorie volume of `1kg` of steam at `100^(@)C=1650xx10^(-3)m^(3)` and 1 atmospheric pressure `=10^(5)Nm^(-2)`)
View SolutionA meteorite weighing `2000kg` enters the earth's atmosphere with a velocity of `1000 km` per second. How many calories of heat will be produced (`J=4.49` joules per calorie).
View SolutionIf a lead bullet be suddenly stopoed and all its energy be used to heat it, with what velocity must the bullet be fired to raise the temperature through `100^(@)C`? (Specific heat capacity of leat `=31.4` calories per kg per kelvin and `J=4.2` joules per calorie.)
View SolutionFrom what height must a block of ice fall to just melt by the impact assuming that half of the heat generated is absorbed by ice? (`J=4.2` joules per calories and `L=80` kilocalories per kg)
View SolutionWith what velocity must a lead bullet at `50^(@)C` strike against an obstacle in order that the heat produced by the arrest of the motion, is sufficient of melt it, assuming that all the heat produced remains within the bullet?
(Specific heat capacity of lead `=31cal kg^(-1)K^(-1)`, melting point of lead `=335^(@)C`, specific latent heat capacity of lead `=5370 cal kg^(-1)K^(-1)` and `J=4.2` joules `cal^(-1)`)
View SolutionA block of ice is dropped into a well of water, both ice and water being at `0^(@)C`. From what height must the ice fall in order that `1//100` of it may melt?
(`L` of ice `=80xx10^(3) calkg^(-1), J=4.2` joules `cal^(-1)` and `g=9.8ms^(-2)`)
View SolutionA hole is drilled into a block of lead of mass `10kg` by a driller. The driller is driven by an electric motor of 30 r.p.m. and the couple exerted by the motor on the driller is `10Nm`. Calculate the rise in temperature of the lead in 10 minutes. `J=4.2` joules `cal^(-1)`. Relative specific heat capacity of lead 0.03 and sp. heat capacity of water `1000 cal kg^(-1)K^(-1)`.
View SolutionA bullet of lead melts when stopped by obstacle. Assuming that 25 per cent of the heat is absorbed by the osbtacle, find the velocity of the bullet if its initial temperature is `27^(@)C`. (Melting point of lead `327^(@)C`, specific heat capacity of lead `=30 cal kg^(-1)K^(-1)` specific latent heat of fusion of lead `=6000 cal kg^(-1)` and `J=4.2` joules `cal^(-1)`)
View SolutionA thermally insulated vessel containing a gas, whose molar mas is equal to `M` and specific heat capacity ratio `gamma`, moves with a velocity `V`. Find the temperature rise when the vessel is stopped suddenly.
View SolutionGaseous hydrogen initially contained under standard conditions in a sealed vessel of volume `5xx10^(-3)m^(-3)` was cooled by `55K`. Find the change in internal energy and amount of heat lost by the gas.
View SolutionTwo lead spheres of masses `10kg` and `30k` approach each other with speeds `10ms^(-1)` and `20ms^(-1)` and collide completely inelastically. What is the heat produced by the collision? What is the rise in temperature if all the heat produced is ratained by the spheres? (Specific heat capacity of lead `=31 cal kg^(-1)K^(-1)` and `J=4.2` joules `cal^(-1)`)
View SolutionA copper calorimeter of mass `0.1kg` is filled with `52g` of kerosene. A resistance wire of resistance 2 ohms is immersed in it and it is observed that there is a `5^(@)C` rise in temperature in 6 minutes when 1 amperes of current is passed through it. Calclate the valule of `J`. Sp. heat capacity of copper `=100 cal kg^(-1)K^(-1)` and sp. heat capacity of kerosene `=500 cal kg^(-1) K^(-1)`.
View SolutionThe anode of a diode valve ils bmbarded by a stream of electrons each of mass `9xx10^(-31)kg` moving with velocity `10^(7)ms^(-1)`. If the mass of anode is `0.5g` and its specific heat capacity `100` cals per kg per kelvin `(J=4.2` joules `cal^(-1)`) and `3xx10^(17)` electrons hit it per second, calculate the rate at which its temperature rises.
View SolutionWater oozes out from a porous pot the pressure inside being 20 atmosphere more than that outside. If the temperature of the water inside be `10^(@)C`, what would be the temperature of the water coming out? (`J=4.2` joules `cal^(-1)`, atmospheric pressure `=1.05xx10^(5)Nm^(-2)`)
View SolutionAs a result of heating a mole of an ideal gas at constant pressure by `72^(@)C`, a heat flow by an amount 1600 joules takes place. Find the work performed by the gas, ther increment of its internal energy, and the value of `gamma`.
View SolutionHow much heat must be supplied to nitrogen in a process of heating at constant pressure that the gas may perform 2 joules of work?
View SolutionTwo moles of a certain ideal gas at `300K` were cooled at constant volume so that the pressure was reduced to half t he initial value. Then, as a result of heating at constant pressure, the gas expanded till its temperature got back ot the initial value. Find the total amount of heat absorbed by the gas in the process.
View SolutionCalculate the value of `gamma` for a gaseous mixture consisting `n_(1)` moles of oxygen and `n_(2)` moles of carbon dioxide. The values of `gamma` for oxygen and carbon dioxide are `gamma_(1)` and `gamma_(2)` respectively. Assume the gases to be ideal.
View SolutionFind how much heat is necesssary to do internal work in converting `1g` of water at the normal boiling point into steam at the same temperature. Latent heat capacity of steam `=540xx10^(3)calkg^(-1)`, volume of `1kg` of steam at `100^(@)C=1.65m^(3)`
View SolutionA gas of adiabatic exponent `gamma` is supplied heat at a constant pressure. Show that in such a process `Delta Q:DeltaW=gamma:1:(gamma-1)`.
View SolutionIn an isobaric heating process in which the temperature canges from `0^(@)C` to `100^(@)C`, a mole of an ideal gal absorbs `Q=3.35kJ`. Find: (a) the value of `gamma` (b) the increment `DeltaU` in the internal energy of the gas, (c) the work `A` done by the gas.
View SolutionA mole of an ideal gas initially at a temperature `T_(1)=290K` expands isobarically until its volume increases 2 times. Next the gas is cooled isochorically to its initial temperature `T_(1)`.Find (a) the incement `DeltaU` in the internal energy of the gas, (b) the work `A` done by the gas (c) the amount of the heat `Q` received by the gas.
View SolutionTwo moles of helium gas `(gamma=5/3)` is initially tat temperature `t_(1)=27^(@)C` and occupies a volume of `V_(1)=20` litres. The gas is first expanded at consant pressure until the volume is doubled. Then it undergoes an adiabatic change until the temperature returns to its initial value. (i) Sketch the process on a `p-V` diagram (ii) what is the final volume and pressure of the gas, (iii) What is the work done by the gas?
View SolutionAt `27^@C` two moles of an ideal monoatomic gas occupy a volume V. The gas expands adiabatically to a volume 2V. Calculate (i) the final temperature of the gas, (ii) change in its internal energy, and (iii) the work done by the gas during this process.
View SolutionA system undregoes a change of state during which `100kJ` of heat is transferred to it and it does `50kJ` of work. The system is brought back to its original state through a process during which `120kJ` of heat is transferred to it. Find the work done by the system in the second process.
View Solution
All Questions questions and complete solutions for chapter FIRST LAW OF THERMODYNAMICS of BHARATI BHAWAN PHYSICS (HINGLISH) of Class 11