Complete Solutions to विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न) of chapter मात्रक, मापन तथा त्रुटि विश्लेषण of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | मात्रक, मापन तथा त्रुटि विश्लेषण |
| KUMAR MITTAL | विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न) |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
दो वर्नियर कैलिपर्स इस तरह से हैं कि उनके मुख्य पैमाने का 1 समी, 10 समभागों में विभाजित है। एक कैलिपर `(C_(1))` के वर्नियर पमाने पर 10 बराबर भाग हैं जो कि मुख्य पैमा के 9 भागों के बराबर है। दूसरे कैलिपर `(C_(2))` के वर्नियर पैमाने पर भी 10 बराबर भाग हैं जो कि मुख्य पैमाने के 11 भागों के बराबर हैं। दोनों कैलिपर्स के पठनों को चित्र में दर्शाया गया है। `C_(1)` तथा `C_(2)` द्वारा मापे गए सही मान (सेमी में) क्रमश: हैं :
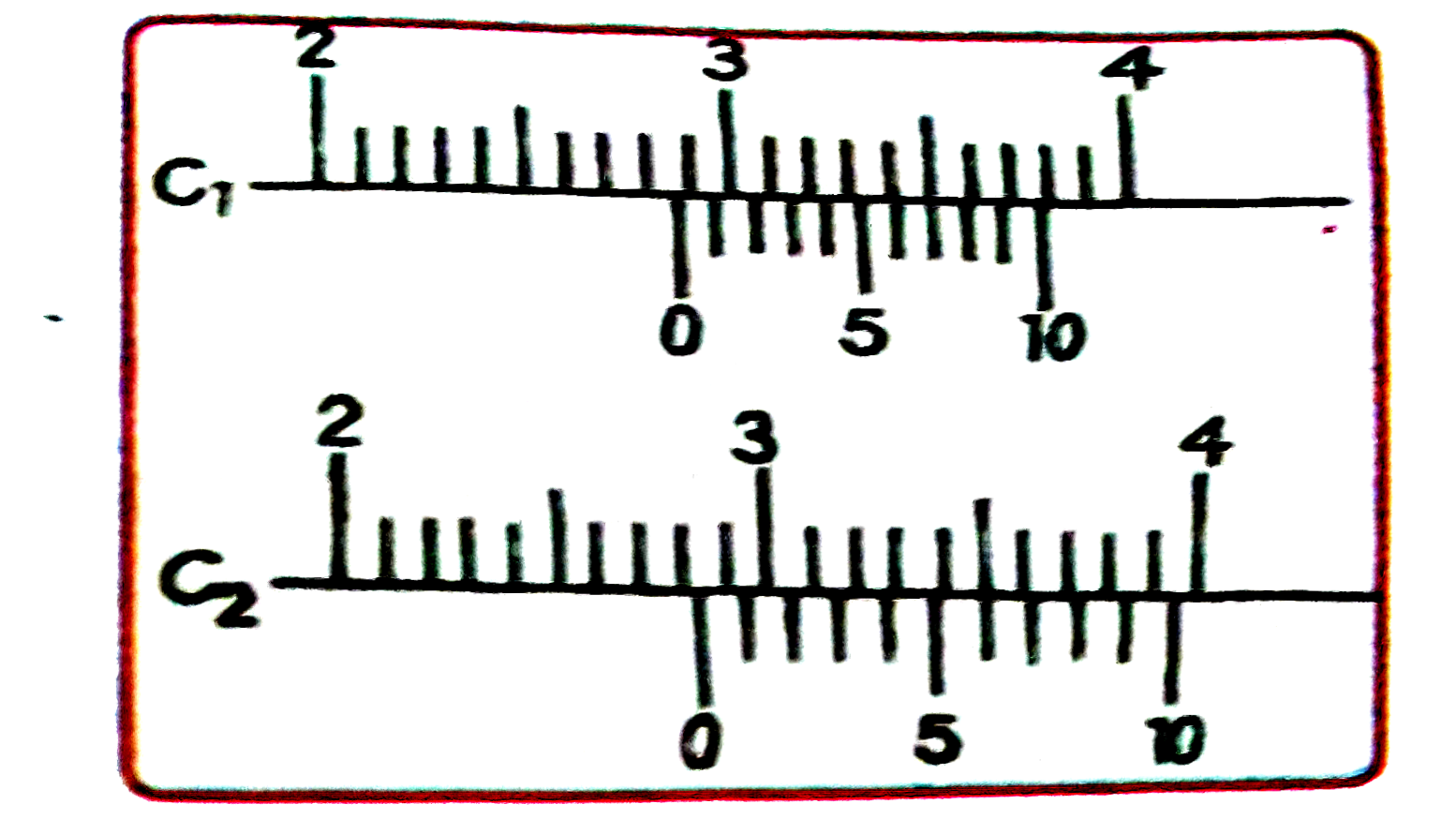
View Solutionएक छात्र एक सरल आवर्त-दोलन के 100 आवृत्तियों का समय चार बार मापता है और उनको 90 s, 91 s, 95 s और 92 s पाता है। प्रयोग की गई घड़ी का न्यूनतम अल्पांश 1 s है। तब मापे गये माध्य समय को उसे लिखना चाहिये :
View Solutionएक प्रसारी गोले (expanding sphere) की तात्क्षणिक (instataneous) त्रिज्या R एवं द्रव्यमान M अचर रहते हैं। प्रसार के दौरान इसका तात्क्षणिक घनत्व `rho` पूरे आयतन में एकसमान रहता है एंव आशिकं घनत्व की दर `((1)/(rho)(rho p)/(dt))` अचर (constant ) है इस प्रसारी आंशिक घनत्व की दर गोले के पृष्ठ पर एक बिन्दु का वेग v निम्न के अनुक्रमानुपाती होगा :
View Solutionएक विद्यार्थी ने एक छड़ की लम्बाई मापकर 3.50 सेमी लिखी। इसको मापने में उसने किस उपकरण का प्रयोग किया?
View Solutionकिसी छात्र ने इस्पात की लघु गेंद के व्यास की माप 0.001 सेमी अल्पतमांक वाले स्क्रूगेज द्वारा की। मुख्य पैमाने की माप 5 मिमी और वृत्तीय पैमाने का शून्य संदर्भ लेवल से 25 माग ऊपर है। यदि स्क्रूगेज में शून्याक त्रुटि -0.004 सेमी है, तो गेद का सही व्यास होगा :
View Solution0.5 mm चूड़ी अन्तराल और वृत्ताकार पैमाने पर 50 भाग वाले एक स्क्रूगेज का प्रयोग एल्यूमीनियम की एक पतली चादर की मोटाई को मापने के लिए किया जाता है। माप शुरू करने से पहले, यह पाया जाता है कि जब स्क्रूगेज के दो जबड़ों को संपर्क में लाया जाता है, तो 45वा भाग मुख्य पैमाने की रेखा के साथ संपाती होता है और मुख्य पैमाने का शून्य काफी मुश्किल से दृश्यमान है। यदि मुख्य पैमाने का पाठ्यांक 0.5 mm और 25वा भाग मुख्य पैमाने की रेखा के साथ संपाती है, तो चादर की मोटाई है:
View Solutionपेंचमापी के वृत्ताकार पैमाने के दो पूर्ण चक्कर मुख्य पैमाने पर 1 मिमी की दूरी चलते हैं। वृत्ताकार पैमाने पर खानों की संख्या कुल 50 है। इसके अतिरिक्त पेंचमापी में शून्यांक त्रुटि -0.03 मिमी पायी जाती है। एक तार का व्यास नापते समय एक विद्यार्थी मुख्य पैमाने पर माप 3 मिमी तथा मुख्य पैमाने की सीधी में वृत्ताकार पेमाने के खानों की संख्या 35 नोट करता है। तार का व्यास है :
View Solutionएक तार का प्रतिरोध इसमें प्रवाहित होने वाली धारा तथा इस पर लगाये विभवान्तर मापन से प्राप्त किया जाता है। यदि धारा तथा विभवान्तर प्रत्येक के मापन में त्रुटि 3% है, तो तार के प्रतिरोध में त्रुटि का मान है।
View Solutionएक प्रिज्म का कोण नापने में प्रयुक्त स्पेक्ट्रोमोटर निम्नलिखित माप देता है। मुख्य पेमाने की माप `= 58.5^@`, वर्नियर की माप = 09 भाग। दिया है मुख्य पेमाने का एक भाग `0.5^@` के बराबर है वर्नियर पर कुल भाग 30 हे और ये मुख्य पैमाने के 29 भागों से मिलते हैं। इन ऑकड़ो से प्रिज्स का कोण है :
View Solutionघन की आकृति वाले किसी पदार्थ का घनत्व, उसकी तीन भुजाओ एवं द्रव्यमान को माप कर, निकाला जाता है। यदि द्रव्यमान एवं लम्बाई को मापने में सापेक्ष त्रुटियां क्रमश: 1.5% तथा 1% हो तो घनत्व को मापने में अधिकतम त्रुटि होगो:
View Solutionत्रिज्या r तथा लम्बाई L के एक तार का द्रव्यमान `M = 0.,3 pm 0.003` ग्राम मापा जाता है। यदि `r= 0.5 pm 0.005` मिमों तथा `L = 6 pm 0.06` सेमी हो, तो इन ऑकड़ों से परिकलित घनत्व में अधिकतम प्रतिशत त्रुटि होगी:
View Solutionकिसी रारल लोलक का आवर्तकाल, `T= 2pi sqrt(T/g)` है L का मापित मान 20.0 सेमी है जिसकी चथार्थंता 1 मिनी है। इस लोलक क 100 दोलनो का समय 90 सेकण्ड है, जिसे 1 सेकण्ड विभेदन का पड़ा से नापा गया है, तो g के निर्धारण में यथार्थता होगी :
View Solutionएक व्यक्ति एक पत्थर को कुएं में गिराते समय और कुएँ की तली में संघट्ट से उत्पन्न ध्वनि के समय अन्तराल का मापन करके कुएँ की गहराई का पता लगाता है। वह समायांतराल के मापन में त्रुटि `deltaT = 0.01` सेकेण्ड एवं कुएँ की गहराई L = 20 m मापता है। गुरुत्वाकर्षण त्वरण `g=10ms^(-2)` एवं ध्वनि गति `300ms^(-1)` दी गई है। `(deltaL)/(L)`के मापन में निकटतम आंशिक त्रुटि (fractional error) है।
View Solutionकेशनली विधि द्वारा पृष्ठ तनाव T ज्ञात करने के प्रयोग में निम्न प्रेक्षण प्राप्त होते हैं -
केशनली का व्यास `D=1.25xx10^(-2)` मीटर, जल का चढ़ाव `h=1.45xx10^(-2)` मीटर तथा `g=9.8` मी/से`.^(2)` । संबंध `T=(rhg)/(2)xx10^(-3)` न्यूटन/मीटर का उपयोग करते हुए पृष्ठ तनाव में संभावित त्रुटि का मान होगा -
View Solutionअनुनाद नलो प्रयोग में, 512 हर्ट्ज आवृत्ति के स्वरित्र द्विभुज के साथ अनुनाद जल के दो उत्तरोत्तर ततों 30.7 सेमी तथा 63.2 सेमी पर प्राप्त होता है। ध्वनि की चाल की गणना करने में अधिकतम। सन्भव त्रुटि है।
View Solutionसलं के प्रयोग में यग प्रत्यास्थिता गुणाक `y=(MLg)/(pi l d^2)` निकालने के लिये एक L= 2 मीटर लम्बे तथा d = 0.5 मिमी व्यास के तार का उपयोग किया गया है। भार M = 2.5 किग्रा लगाने पर तार की लम्बाई में l = 0.25 मिमी की बृद्धि हुई। cd तथा । के नापने के लिये क्रमशः स्क्रूगेज तथा माइक्रोमीटर का उपयोग किया गया। दोनों के पिच 0.5 मिमी एवं दोनों के वृत्ताकार पैमाने पर 100 निशान हैं। Y के ज्ञात करने में अधिकतम प्रसम्भाव्य त्रुटि में :
View Solutionएक बेलन का व्यास एक वर्नियर कैलीपर्स से जिसमें कोई शून्य त्रुटि नहीं है, नापा जाता है। यह पाया जाता है कि वर्नियर पैमाने का शून्य 5.10 सेमी तथा 5.15 सेमी के बीच मुख्य पैमाने पर पाया जाता है। वर्नियर पैमाने के 50 भाग 2.45 सेमी के तुल्य हैं। वर्नियर पैमाने का 24वाँ भाग मुख्य पैमाने के किसी भाग से ठीक संपाती है। बेलन का व्यास है :
View Solutionएक प्रयोग से एक ठोस गेंद का घनत्व निर्धारित करना है। गेंद का व्यास एक स्क्रूगेज द्वारा मापा जाता है, जिसका पिच 0.5 मिमी तथा जिसके वृतीय पैमाने पर 50 भाग हैं। माप में मुख्य पैमाने पर पाठ्याकं 2.5 मिमी तथा वृतीय पैमाने पर 20 भाग हैं। यदि गेंद के मापे गये द्रव्यमान में सापेक्ष त्रुटि 2% है, तब घनत्व में सापेक्ष प्रतिशत त्रुटि है :
View Solutionव्यंजक `2d sin theta = lambda ` . प्रयुक्त करने पर, संगत कोण 0, 0 से 90° के range में नापकर कोई d का मान ज्ञात करता है। तरंगदैर्घ्य 2. सही ज्ञात है तथा 0 में त्रुटि 0 के सभी मानों के लिये नियत है। जैसे ही 0, 0 से बढ़ता है :
View Solution
विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ठ प्रकार प्रश्न) questions and complete solutions for chapter मात्रक, मापन तथा त्रुटि विश्लेषण of NAGEEN PHYSICS (HINDI) of Class 11