Complete Solutions to वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार) of chapter सदिश विश्लेषण एवं प्रक्षेप्य गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | सदिश विश्लेषण एवं प्रक्षेप्य गति |
| KUMAR MITTAL | वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार) |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
तीन वेक्टर `vecP, vecQ` एवं `vecR` चित्र द्वारा दर्शाये गये है | `vecR` वेक्टर पर एक बिंदु S दर्शाया गया है | बिंदु P एवं बिंदु S के बीच विस्थापन `bvecR` है | `vecP, vecQ` एवं `vecS` वेक्टर के बीच सम्बन्ध है :
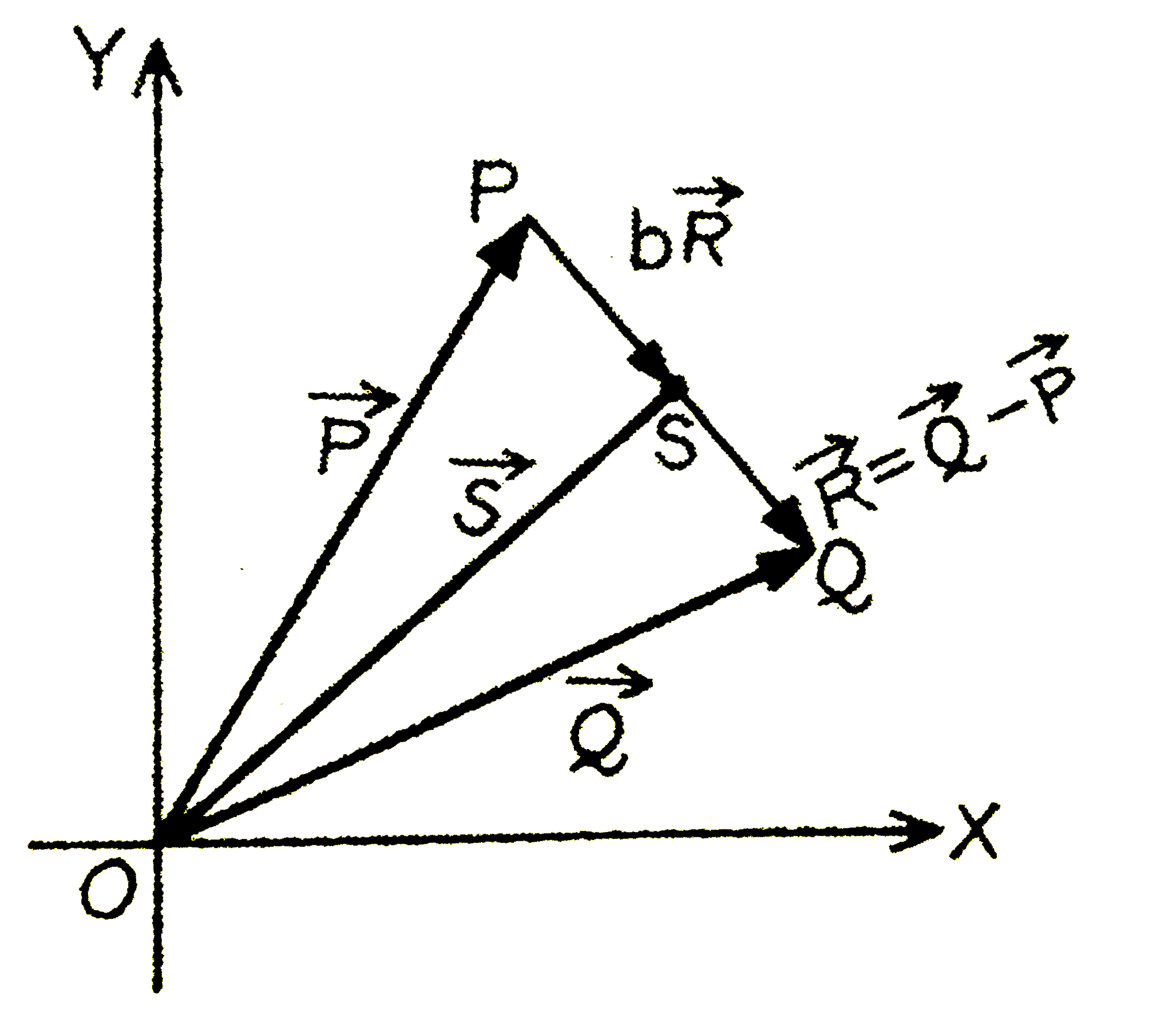
View Solutionसदिश `2hati + 3hatj` तथा Y-अक्ष के बीच कोण है :
View Solution`(1)/(2)(hati + sqrt(3)hatj)` दिशा में चलें वाली प्रकाश की एक किरण एक समतल दर्पण पर आपतित होती है | प्रवर्तन के पश्चात, यह `(1)/(2)(hati -sqrt(3)hatj)` दिशा में चलती है | आपतन कोण है :
View Solutionदो वेक्टर `vecA = hati + 2hatj + 2hatk` तथा `vecB = 3hati + hatj + 2hatk` दिये गये है एक अन्य वेक्टर `vecC` जिसका परिमाण वेक्टर `vecB` के परिमाण के बराबर है तथा दिशा वह है जो `vecA` की है | तब निम्न में जो `vecC` को व्यक्त करता है, वह वेक्टर है :
View Solution1 किग्रा द्रव्यमान का एक पिण्ड किसी कलाश्रित बल `vecF = (2t hati + 3t^(2)hatj)` के आधीन गति आरंभ करता है, तो समय में इस बल द्वारा विकसित शक्ति होगी :
View Solutionयदि दो सदिशों के योग का परिमाण उन दो सदिशों के परिमाण के बराबर है, तो इन सदिशों के बीच कोण है :
View Solutionएक कण इस प्रकार गति करता है कि इसके स्थिति निर्देशांक `(x,y)` निम्न प्रकार है : ltbgt (2 मी, 3 मी) समय t = 0 पर
(6 मी, 7 मी) समय t = 2 सेकण्ड पर (13 मी, 14 मी) समय t = 5 सेकण्ड पर |
तो t = 0 से t = 5 सेकण्ड तक औसत वेग सदिश `(vecc_(av))` होगा :
View SolutionX-Y-तल में गतिमान एक कण पर एक बल `vecF = -k(y hati + x hatj)` (जहाँ k एक धन नियतांक है ) लगता है | मूल-बिंदु से प्रारम्भ करके, कण को धनात्मक X-अक्ष के अनुदिश बिंदु (a,0 ) तक ले जाया जाता है तथा फिर Y-अक्ष के समांतर बिंदु (a, a) तक | कण पर बल `vecF` द्वारा किया गया कुल कार्य है :
View Solutionएक कण X-Y-तल में एक ऐसे बल के प्रभाव में चलता है कि कण का रेखीय संवेग `vecp(t) = A[hati cos( k t ) - hatj ( sin k t )]` है, जहाँ A तथा k अचर है | बल तथा संवेग के बीच का कोण है :
View Solutionयदि वेक्टर `vecA = cos omegat hati + sin omegat hatj` तथा वेक्टर `vecB = cos""(omegat)/(2)hati + sin ""(omegat)/(2)hatj` समय के फलन है तब समय t का वह मान क्या होगा जिस पर ये वेक्टर परस्पर लंबकोणिक (orthogonal) होंगे :
View Solutionकोई कण इस प्रकार गमन करता है कि उसका स्थिति सदिश `vecr = cos omegat hatx + sin omegat haty` द्वारा निरूपित होता है, यहाँ `omega` नियतांक है | निम्न में से कौन-सा कथन सत्य है ?
View Solutionसमय के फलन के रूप में किसी कण का स्थिति सदिश `vecR` दिया गया है :
`vecR = 4 sin (2pit) hati + 4 cos (2 pi t) hatj`
जहाँ, R मीटर से तथा t सेकण्ड में है ओर `hati` तथा `hatj` क्रमशः X-तथा Y-दिशाओं के अनुदिश एकांक सदिश है | इस कण की गति के लिये निम्नांकित में से कौन-सा कथन सही नहीं है |
View Solutionएक गोला एक तोप द्वारा u वेग से क्षैतिज से `theta` कोण पर R दूरी पर एक पहाड़ी की ओर देगा जाता है | पहाड़ी की तली से कितनी ऊँचाई पर गोला टकरायेगा ?
View Solutionm द्रव्यमान का एक क्षैतिज से `alpha` कोण पर प्रारंभिक चल `u_(0)` से जमीन प्रक्षेपित किया जाता है | प्रक्षेप-पथ के उच्चतम बिंदु पर, यह एक अन्य समरूप कण से पूर्णतः अप्रत्यास्थ संघट्ट करता है, जो जमीन से उसी प्रारम्भिक चल `u_(0)` से ऊपर की ओर ऊर्ध्वाधर फेका जाता है | संघट्ट के तुरंत बाद संयुक्त निकाय क्षैतिज से कोण बनता है :
View Solutionएक प्रक्षेप्य को पृथ्वी की सतह से 5 मी/से के वेग से तथा क्षैतिज दिशा से `theta` कोण पर छोड़ा जाता है | किसी अन्य ग्रह से 3 मी/से के वेग तथा इसी कोण `(theta)` पर छोड़े गये एक प्रक्षेप्य पथ, पृथ्वी से छोड़े गये प्रक्षेप्य पथ के सर्वसम ( सर्वथा समान ) है | यदि पृथ्वी पर `g = 9.8` मी/से`""^(2)` है, तो इस ग्रह पर गुरुत्वीय त्वरण का मान मी/से`""^(2)` में होगा :
View Solutionऊँचाई H की एक मीनार से चाल u से एक कण को ऊर्ध्वाधर ऊपर ऊपर की ओर फेंका जाता है कण को पृथ्वी तक गिरने में लगा समय उसके उच्चतम बिन्दु तक पहुँचने के समय का n गुना है H,u एवं n के बीच सम्बन्ध है :
View Solutionएक कण का वेग `vecv = ( yhati + x hatj )` से चल रहा है, जहा k नियतांक है | इसके पथ की सामान्य समीकरण है :
View Solutionएक पिंड को जमीन से `vecv = 9 3hati + 10 hatj)` मी/से वेग से प्रक्षेपित किया जाता है | पिण्ड द्वारा प्राप्त महत्तम ऊँचाई तथा क्षैतिज परास क्रमशः है ( दिया है g = 10 मी/से`""^(2)`)
View Solutionएक प्रक्षेप्य को प्रारंभिक वेग `(hati + 2hatj)` मी/से दिया जाता है, जहाँ `hati` जमीन के अनुदिश है तथा `hatj` ऊर्ध्वाधर के अनुदिश है | यदि g = 10 मी/से`""^(2)` हो, तो प्रक्षेप-पथ की समीकरण है :
View Solutionएक लड़का एक पत्थर को अधिकतम 10 मीटर की ऊँचाई तक फेंक सकता है। उस लड़के द्वारा फेंकी जा सकने वाली अधिकतम क्षैतिज दुरी होगी :
View Solutionएक द्रव्यमानहीन स्प्रिंग की तनावहीन लम्बाई 4.9 सेमी है | इसका एक सिरा बँधा है तथा दूसरे पर एक छोटा गुटका लगा है (चित्र) | यह निकाय एक घर्षणहीन क्षैतिज तल पर रखा है | समय t = 0 पर गुटके को 0.2 मीटर खींचकर स्थिर अवस्था से छोड़ा जाता है, तब यह कोणीय आवृत्ति `omega = (pi)/(3)` रेडियन/सेकण्ड से सरल आवर्त गति
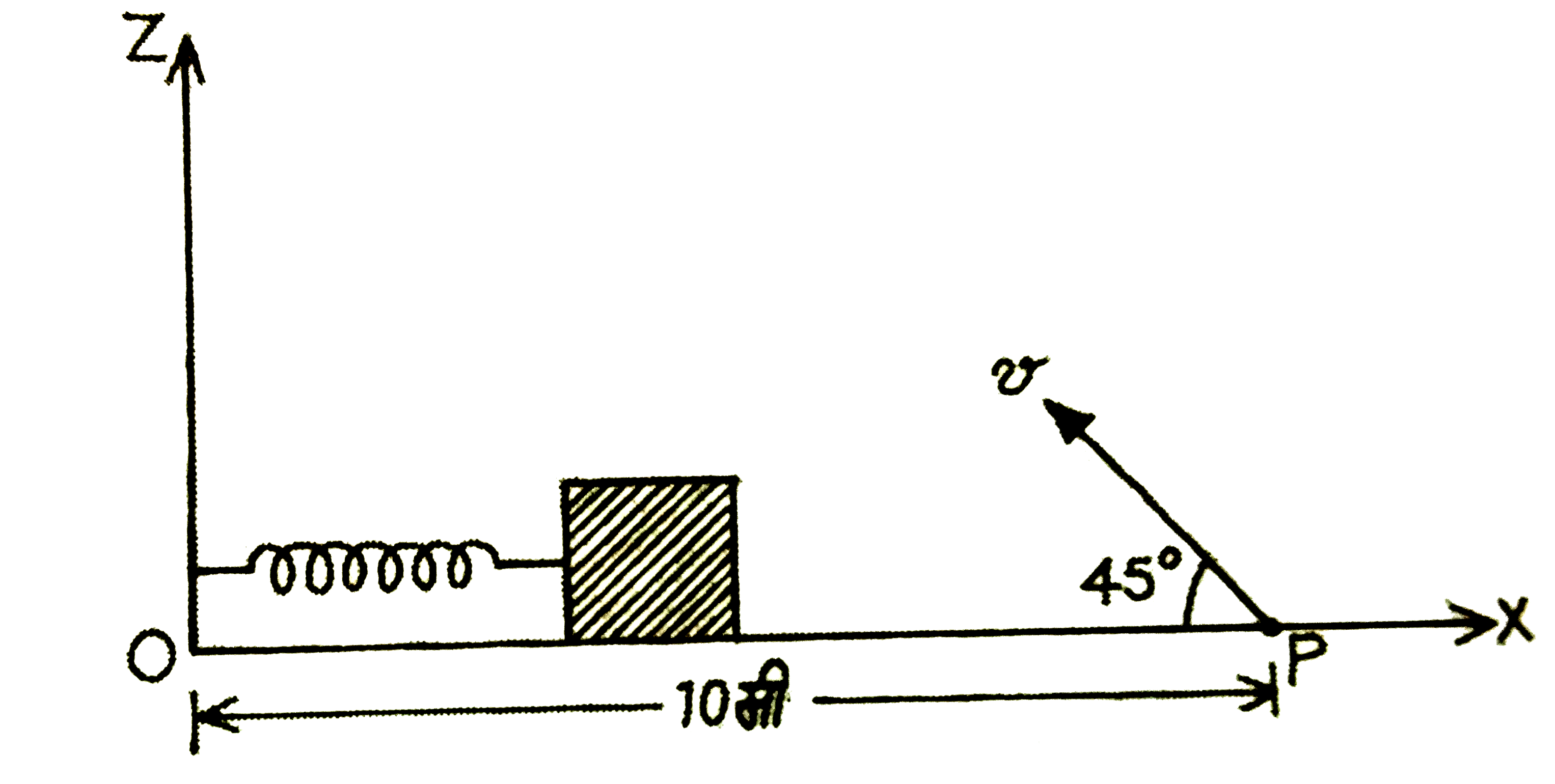
करता है | ठीक उसी समय (t = 0) पर एक छोटा कंकड़ v चाल से बिन्दु P पर क्षैतिज से `45^(@)` के कोण पर प्रक्षपित किया जाता है, बिन्दु P को बिन्दु O से क्षैतिज दूरी 10 मीटर है | यदि t = 1 सेकण्ड पर कंकड़ गुटके पर गिरता है, तथा का मान है ( g = 10 मी/से`""^(2)`)
View Solutionपानी का एक फव्वारा धरती पर अपने चारो ओर पानी छिड़कता है, यदि फव्वारे से निकल रहे पानी की चाल `v` है, तब फव्वारे के चारो ओर गीला होने वाला कुल क्षेत्रफल है :
View Solutionएक जहाज A, 10 किमी/घंटा की चाल से पश्चिम दिशा की ओर गति कर रहा है | एक अन्य जहाज B, इस जहाज A से 100 किमी दक्षिण दिशा में है ओर 10 किमी/घंटा की चाल से उत्तर दिशा की ओर जा रहा है इन दोनों के बीच की दूरी कितने समय पश्चात न्यूनतम हो जायेगी ?
View Solution
वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार) questions and complete solutions for chapter सदिश विश्लेषण एवं प्रक्षेप्य गति of NAGEEN PHYSICS (HINDI) of Class 11