Complete Solutions to विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ट प्रकार के प्रश्न) of chapter दृढ़ पिण्डों की घूर्णन गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | दृढ़ पिण्डों की घूर्णन गति |
| KUMAR MITTAL | विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ट प्रकार के प्रश्न) |
| Number Of Questions | 50 |
| Academic Year | 2023-24 |
एक द्रव्यमान `M` एवं लम्बाई `l` की पतली एवं एकसमान छड़ का एक सिरा धुराग्रस्त है जिससे कि वह एक ऊर्ध्वाधर समतल में घूम सकती है। धुरी का घर्षण नगण्य है। छड़ के दूसरे सिरे को धूरी के ऊपर ऊर्ध्वाधर रखकर छोड़ दिया जाता है । जब छड़ ऊर्ध्व से `theta` कोण बनाती है तो उसका कोणीय त्वरण होगा:

View Solutionएक खोखले सिलिण्डर का द्रव्यमान 3 किग्रा तथा त्रिजया 40 सेमी हैं इस पर एक डोरी लपेट दी गई है। यदि डोकरी को `30N` के बल द्वारा खींचा जाये तो, सिलिण्डर का कोणीय त्वरण कितना होगा?
View Solutionएक त्रिज्या `R` एवं द्रव्यमान `M` का पहिया एक `R` ऊंचाई वाले द़ढ़ सोपान के तल पर रखा है (जैसे की चित्र में दिखाया गया है) । पहिये को सोपान पर चढ़ाने मात्र के लिए एक अचन बल पहिये के पृष्ठ पर सतत कार्यरत है। कागज के पृष्ठ से अभिलम्ब दिशा में बिंदु `Q` से जाने वाली अक्ष के सापेक्ष बल आघूर्ण `tau` मानिये। निम्न में से कौन से प्रकथन सही है?

View Solutionस्पर्श रेखीय बल `F=(20t-5t^(2))` न्यूटन (जहां `t` सेकण्ड में नापा गया है) के कारण 2 मीटर त्रिज्या की एक घिरनी अपनी अक्ष पर घूमती है। यदि घिरनी का अपनी घूर्णन अक्ष के परितः जड़त्व-आघूर्ण 10 `kg-"metre"^(2)` है तब घिरनी की गति की दिशा प्रतिलोमित होने से पहले घिरनी द्वारा लगाये गये चक्करों से संख्या है:
View Solutionत्रिज्या `R` द्रव्यमान `m` के एक एक समान खोखले बेलन के चारो ओर एक द्रव्यमानविहीन डोरी से एक द्रव्यमान `m` अवलंबित है। यदि डोरी बेलन पर फिसलती नहीं है तब छोड़े जाने पर द्रव्यमान किस त्वरण से गिरेगा?
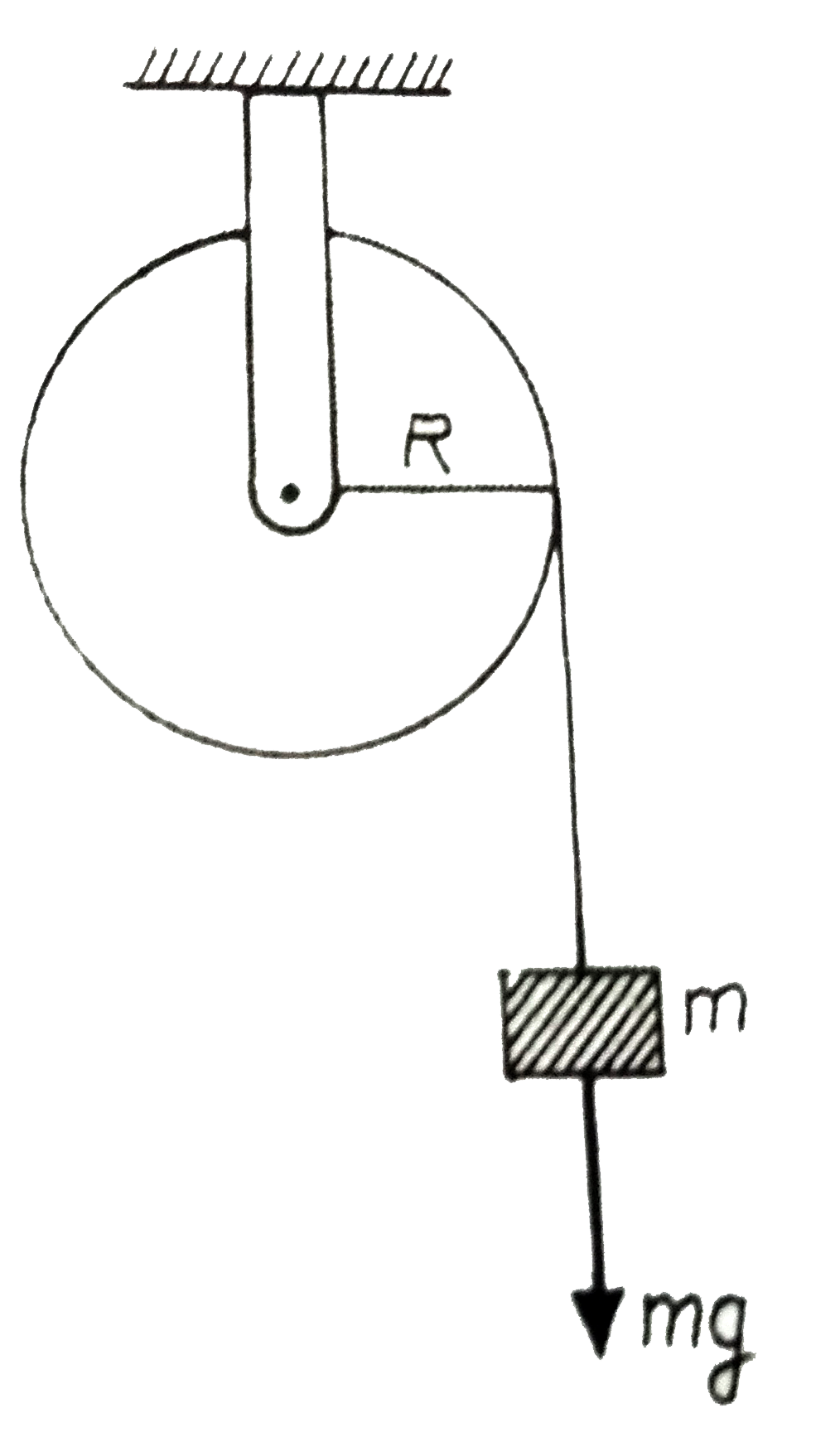
View Solution50 किग्रा द्रव्यमान तथा 0.5 मीटर त्रिज्या का एक ठोस सिलिन्डर (बेलन) अपनी क्षैतिज अक्ष के परितः स्वतंत्र रूप से घूर्णन कर सकता है। इस पर एक भारहीन रस्सी लपेटी गयी हे जिसका एक सिरा एक सिलिन्डर से जुड़ा है और दूसरा सिरा मुक्त रूप से लटक रहा है। रस्सी में कितना तनाव लगाया जाये कि कोणीय त्वरण 2 परिक्रमण `"second"^(-2)` हो?
View Solutionबिंदु `(2,0,-3)` पर कार्यरत बल `vecF=4hati+5hatj-6hatk` का बिंदु (2,-2,-2) के परितः आघूर्ण होगा:
View Solutionएक छड़ का भार `W` है। यदि दो समांतर क्षुरधारों `A` तथा B पर टिकी है तथा क्षैतिज अवस्था में संतुलन में हैं। यदि A तथा B के बीच की दूरी `d` है तथा छड़ का द्रव्यमान केंद्र A से x दूरी पर है तो A पर अभिलम्ब प्रतिक्रिया का मान होगा?
View Solutionविरामावस्था में स्थित 50 सेमी त्रिज्या की एक एकसमान वृत्ताकार डिस्क अपने तल के लम्बवत और केंद्र से गुजरने वाली अक्ष के परितः घूमने के लिए स्वतंत्र हैं। डिस्क पर कोई बल आघूर्ण कार्य करता है जो इसमें 2.0 `"radian"//"second"^(2)` का कोणीय त्वरण उत्पन्न करता है 2.0 सेकण्ड पश्चात `m//s^(2)` में इसमें नैट त्वरण लगभग होगा:
View Solutionतार के बने एक आयताकार फ्रेम जिसका द्रव्यमान नगण्य है तथा भुजाएं `a` तथा `b(agtb)` है के चारों कोनों पर द्रव्यमान `m` के चार छोटे पिण्ड रखे गये हैं। अब यदि तार फ्रेम को `b` लम्बाई की भुजा के अनुदिशा अक्ष के परितः घुमाया जाये, तब निकाय का इस घूर्णन अक्ष के परितः जड़त्व-आघूर्ण होगा:
View Solutionएक हल्की छड़ की लम्बाई `l` है। इसके दो सिरों पर `m_(1)` व `m_(2)` द्रव्यमान के पिण्ड संलग्न है। इस छड़ के लम्बवत इसके संहति केंद्र से गुजरने वाली अक्ष के परितः इस निकाय का जड़त्व आघूर्ण होगा:
View Solutionलम्बाई `l` तथा त्रिज्या `R` के एक ठोस बेलन का अपनी ज्यामितीय अक्ष के परितः जड़त्व-आघूर्ण उतना ही है जितना कि निरक्षीय अक्ष के परितः है। `R` तथा `l` का अनुपात है
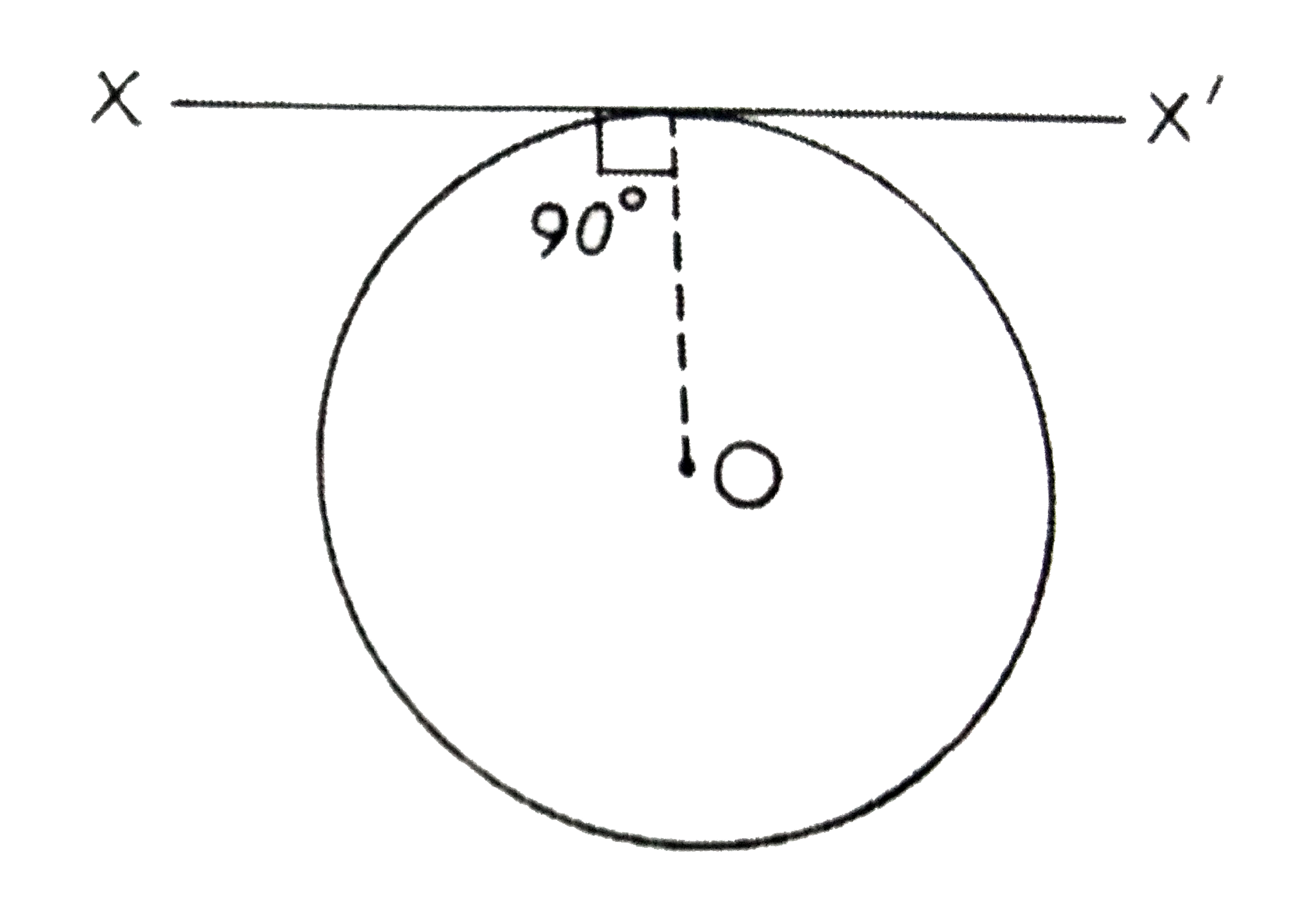
View Solutionतीन सर्वसम गोलीय कोशों में प्रत्येक कोशों में प्रत्येक का द्रव्यमान `m` तथा त्रिज्या `r` है। इन्हें आरेख में दर्शाये गये अनुसार रखा गया है। `XX’` एक अक्ष है। जो दो गोलीय कोशों को स्पर्श करती है तथा तीसरे के व्यास से होकर गुजरती है। `XX’` अक्ष के परितः इन तीन गोलीय कोशों के निकाय का जड़त्व आघूर्ण होगा:

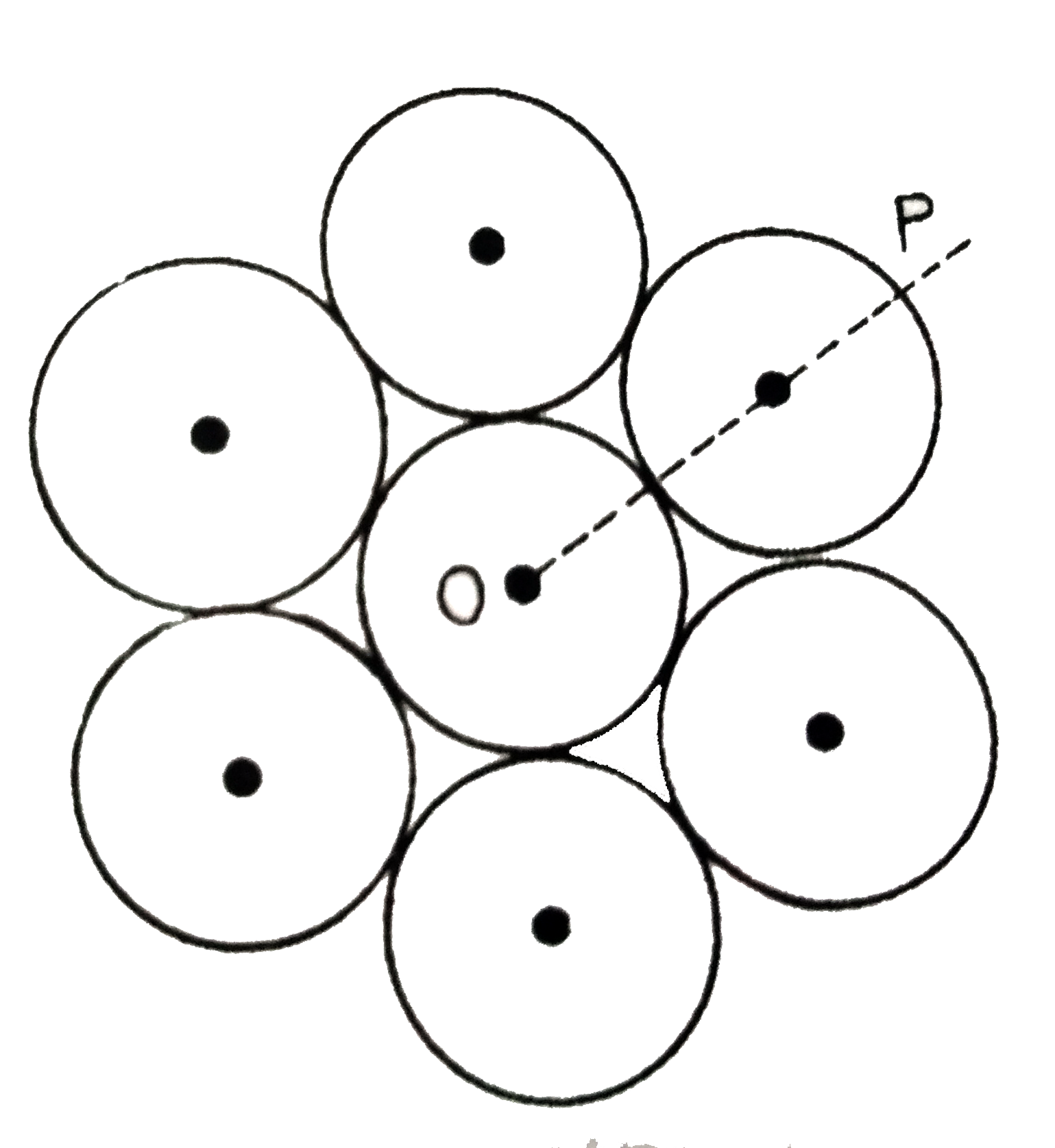
View Solutionचित्रानुसार सात एक जेकसी वृत्ताकार समतल डिस्कों, जिनमें प्रत्येक का द्रव्यमान `M` तथा त्रिज्या `R` है को सममित रूप से जोड़ा जाता है। समतल के लम्बवत तथा `P` से गुजरने वाली अक्ष के सापेक्ष इस संयोजन का जड़त्व आघूर्ण है:
View Solutionत्रिज्या `R` की एक वृत्ताकार डिस्क का एक –चौथाई भाग काटा कर, इस भाग को मूल डिस्क के केंद्र से गुजरने वाली तथा डिस्क के पृष्ठ के लम्बवत अक्ष के परितः घुमाया जाता है। यदि डिस्क के काटे गये भाग का द्रव्यमान `M` हो तब इसका घूर्णन-कक्ष के परितः जड़त्व-आघूर्ण होगा:

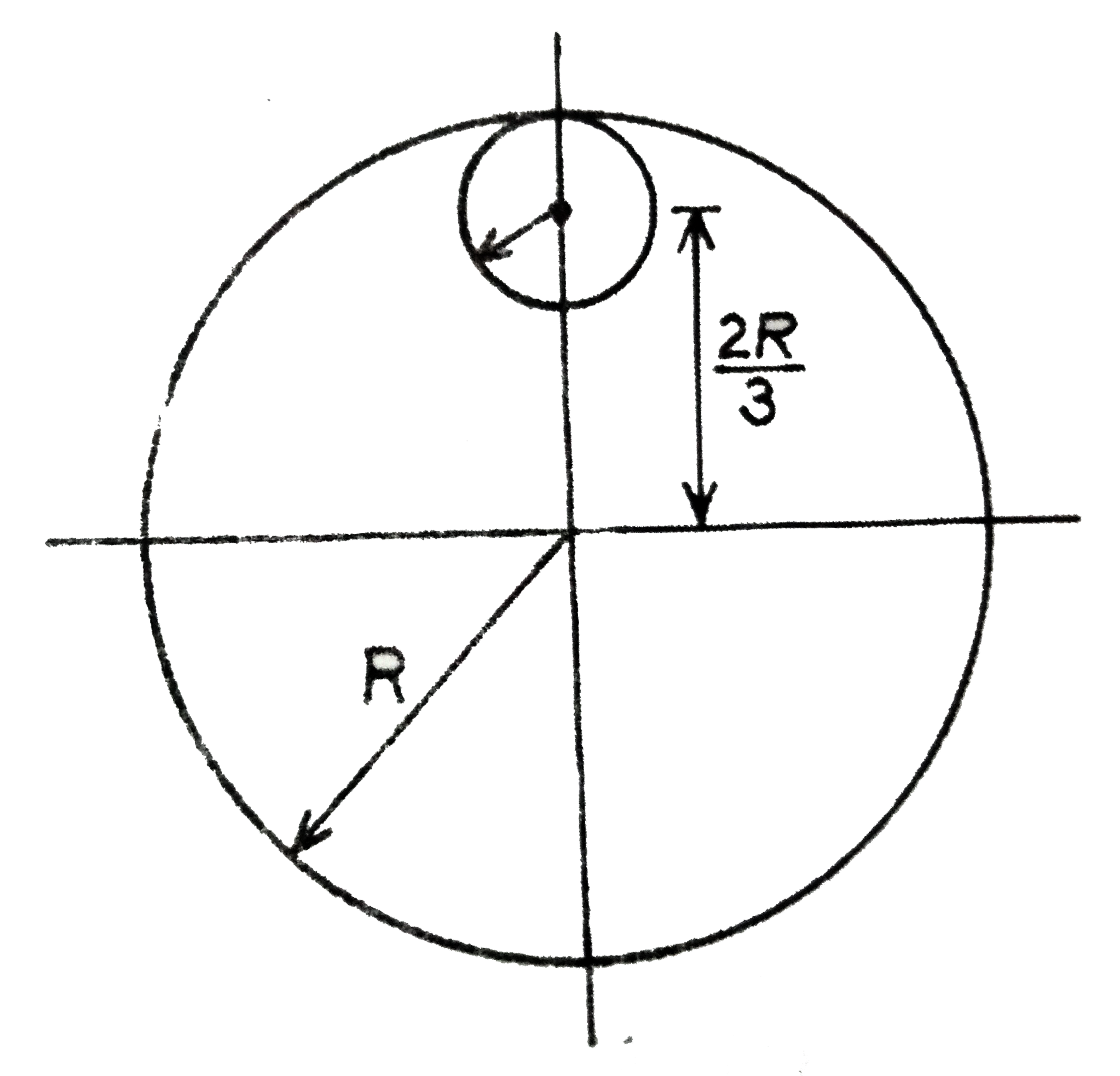
View Solution`R` त्रिज्या तथा `9M` द्रव्यमान के एकचसमान गोलाकार डिस्क से `R//3` त्रिज्या का एक छोटा गोलाकार डिस्क काट कर निकाल लिया जाता है जैसा कि चित्र में दर्शाया गया है। डिस्क के सतह के लम्बवत एवं उसके केंद्र से गुजरने वाले अक्ष के सापेक्ष बची हुई डिस्क का जड़त्व आघूर्ण होगा:
View Solutionद्रव्यमान `M` तथा त्रिज्या `R` की किसी डिस्क से `R` व्यास का कोई वृत्ताकार छिद्र इस प्रकार काटा जाता है कि उसकी रिम डिस्क के केंद्र के गुजरे। डिस्क के शेष भाग का डिस्क के लम्बवत उसके केंद्र से गुजरने वाली अक्ष के परितः जड़त्व आघूर्ण है।
View Solutionकिसी ठोस गोले का द्रव्यमान `M` तथा इसकी त्रिज्या `R` है। इसमें से अधिकतम सम्भव आयतन का एक घन काट लिया जाता है। इस घन का जड़त्व आघूर्ण कितना होगा, इसकी घूर्णन अक्ष, इसके केंद्र से होकर गुजरती है तथा इसके किसी एक फलक के लम्बवत है?
View Solutionलम्बाई `L` तथा एकसमान रेखीय द्रव्यमान घनत्व `m` वाले एक तार को वृत्तीय लूप में चित्रानुसार मोड़ा गया है। लूप का केंद्र `O` है। स्पर्शरेखीय अक्ष `XX’` के परितः लूप का जड़त्व आघूर्ण है
View Solutionएक मीटर की छड़ फर्श पर ऊर्ध्वाधर खड़ी है। इसका एक सिरा फर्श पर टिका है। जब यह गिरती है तो इसके ऊपर के सिरे का चाल फर्श से टकराने पर होगी (यह मानकर कि छड़ का सिरा फर्श पर फिसलता नहीं हैं तथा `g=9.8 "metre"//"second"^(2)`)
View Solutionएक दृढ़ ठोस गोला बिना किसी बाह्य बल-आघूर्ण के किसी अक्ष के परितः चक्रण कर रहा है। ताप –परिवर्तन के कारण इसका आयतन 1 प्रतिशत बढ़ जाता है। इसका कोणीय वेगः
View Solutionएक मोटर वाहन किसी सड़क पर 54 किमी/घण्टा की चाल से चल रहा है। इसके पहियों की त्रिज्या 0.45 मीटर है और घूर्णन अक्ष के परितः पहिये का जड़त्व आघूर्ण 3 किेग्रा `m^(2)` है। यदि ब्रेक लगाने के बाद, वाहन को रूकने में 15 सेकण्ड का समय लगता है तो ब्रेक द्वारा पहिये पर लगा औसत बल आघूर्ण का मान होगा:
View Solutionएक चिकना गोला A घर्षणहीन तल पर कोणीय चाल `omega` से तथा द्रव्यमान-केंद्र वेग `v` से गति कर रहा है। यह विराम अवस्था में स्थित समरूप गोले `B` से प्रतयास्थ रूप से सीधे टकराता है। सभी स्थानों पर घर्षण नगण्य है। टकराने के बाद यदि गोलों की कोणीय चाले क्रमश: `omega_(A)` तथा `omega_(B)` है तब
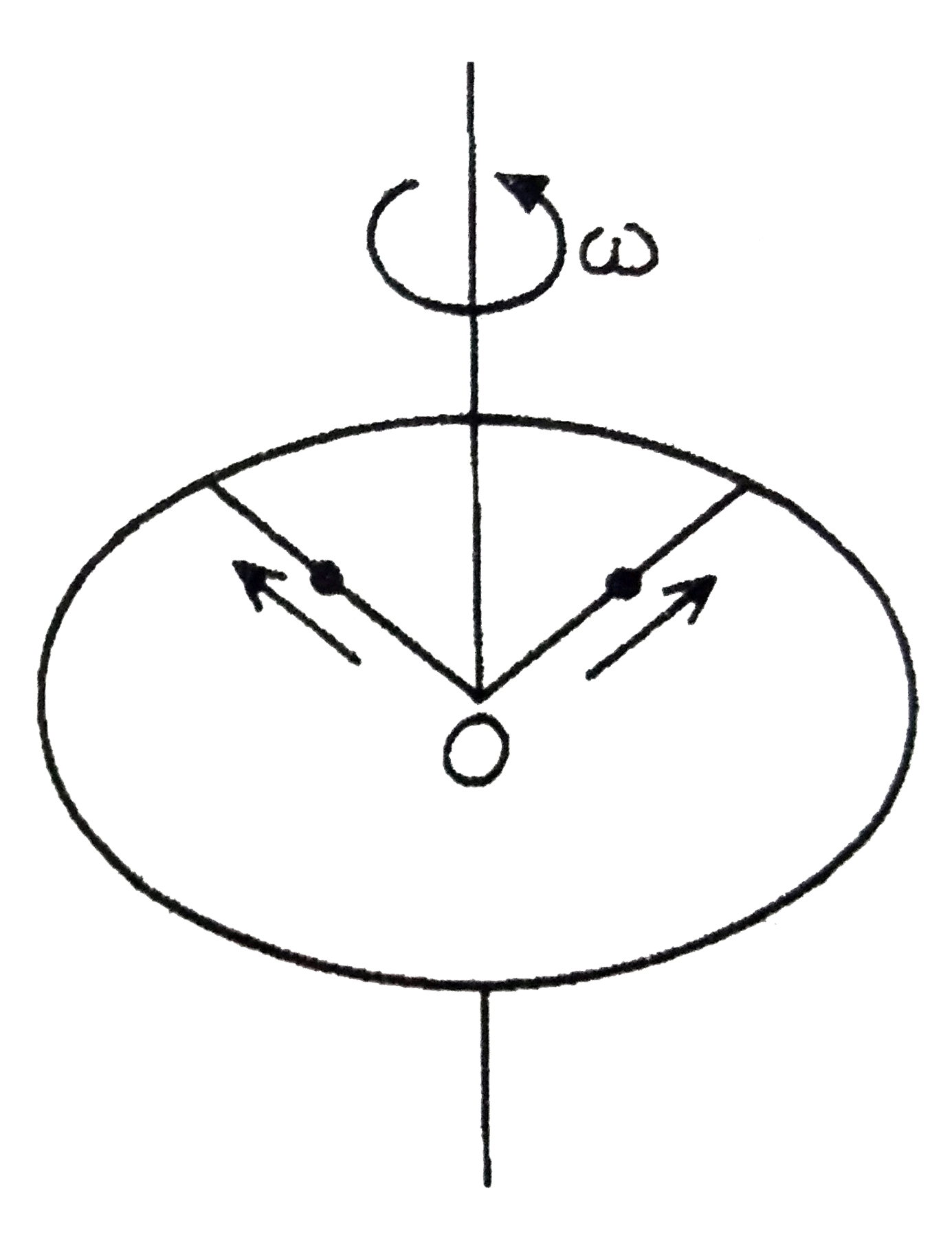
View Solutionद्रव्यमान `M` तथा त्रिज्या `R` की एक पतली वृत्ताकार वलय अपनी अक्ष के परितः नियत कोणीय वेग `omega` से घूर्णन कर रही है। दो वस्तुयें प्रत्येक का द्रव्यमान `m` वलय के व्यास के विपरीत सिरों पर धीरे से रख दी जाती है। अब वलय से घूमने का कोणीय वेग है:
View Solutionएक बच्चा अपने हाथ मोड़कर, केन्द्रीय अक्ष के परितः घूमते एक प्लेटफॉर्म के केंद्र पर खड़ा है। निकाय की गतिज ऊर्जा `K` है। बच्चा अपनी भुजायें फैला देता हैं जिससे कि निकाय का जड़त्व आघूर्ण दोगुना हो जाता है निकाय की गई ऊर्जा है
View Solutionद्रव्यमान `M` तथा त्रिज्या `R` का एक ठोस गोला अपने व्यास के परितः घूर्णन कर रहा है। इसी द्रव्यमान तथा इसी त्रिज्या का एक ठोस बेलन भी अपनी ज्यामितीय अक्ष के परितः घूर्णन कर रहा है। बेलन के घूर्णन की कोणीय चाल गोले से दोगुनी है। इन दोनों की घूर्णन गतिज ऊर्जाओं का अनुपात होगा:
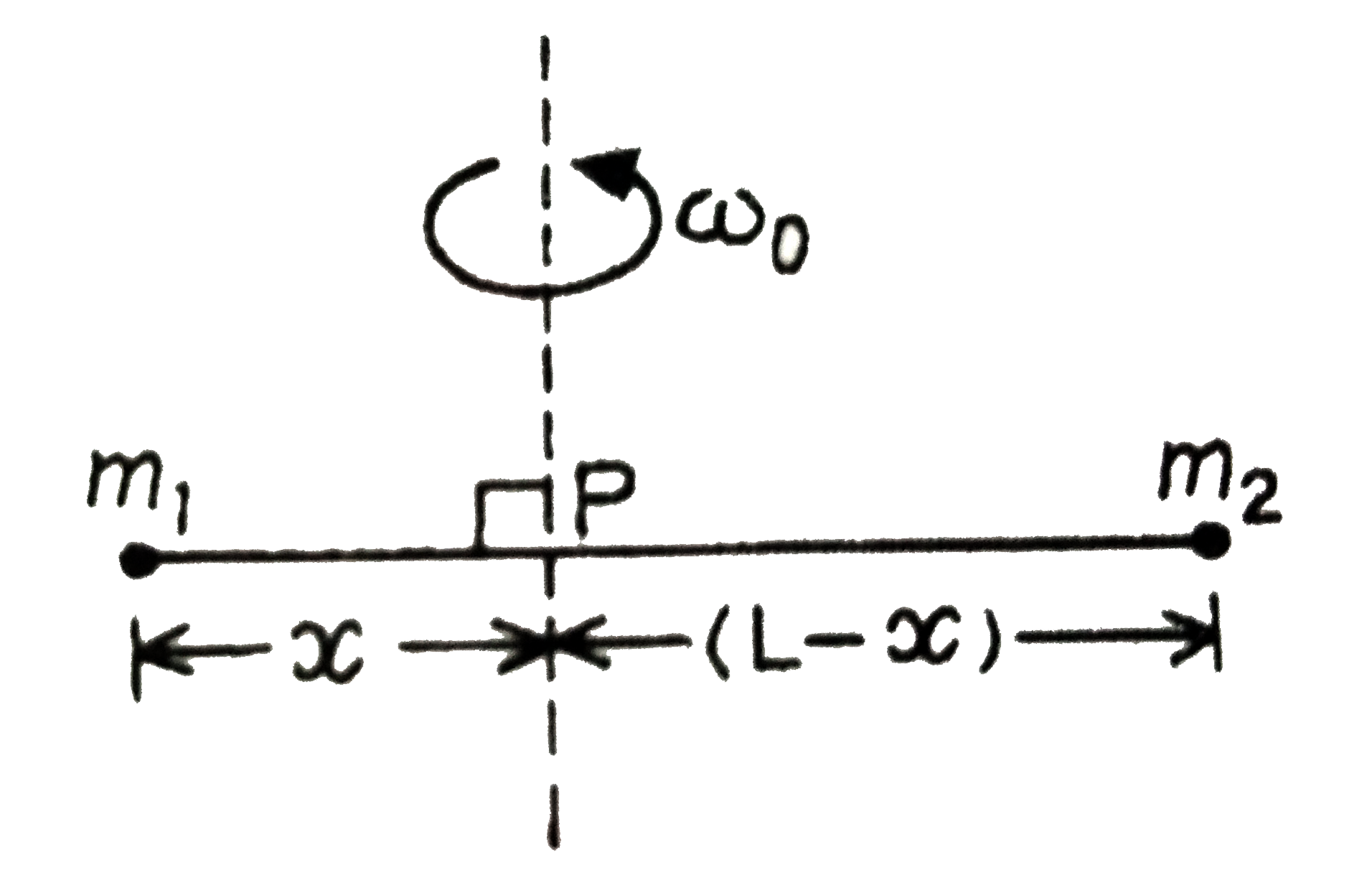
View Solutionकिसी दृढ़ छड़ की लम्बाई `L` है और इसका द्रव्यमान नगण्य है। इसके दो विपरील सिरों पर क्रमशः `m_(1)` तथा `m_(2)` द्रव्यमान के दो बिंदु पिण्ड रखे गये हैं। इस छड़ को उसके स्वयं को लम्बवत अक्ष के परितः घूर्णन कराना है जो छड़ पर स्थित किसी बिंदु `P` से होकर गुजरती है तो बिंदु `P` की वह स्थिति जिसके कलए छड़ को कोणीय वेग `omega_(0)` से घूर्णन कराने के लिए आवश्यक कार्य न्यूनतम होगा है
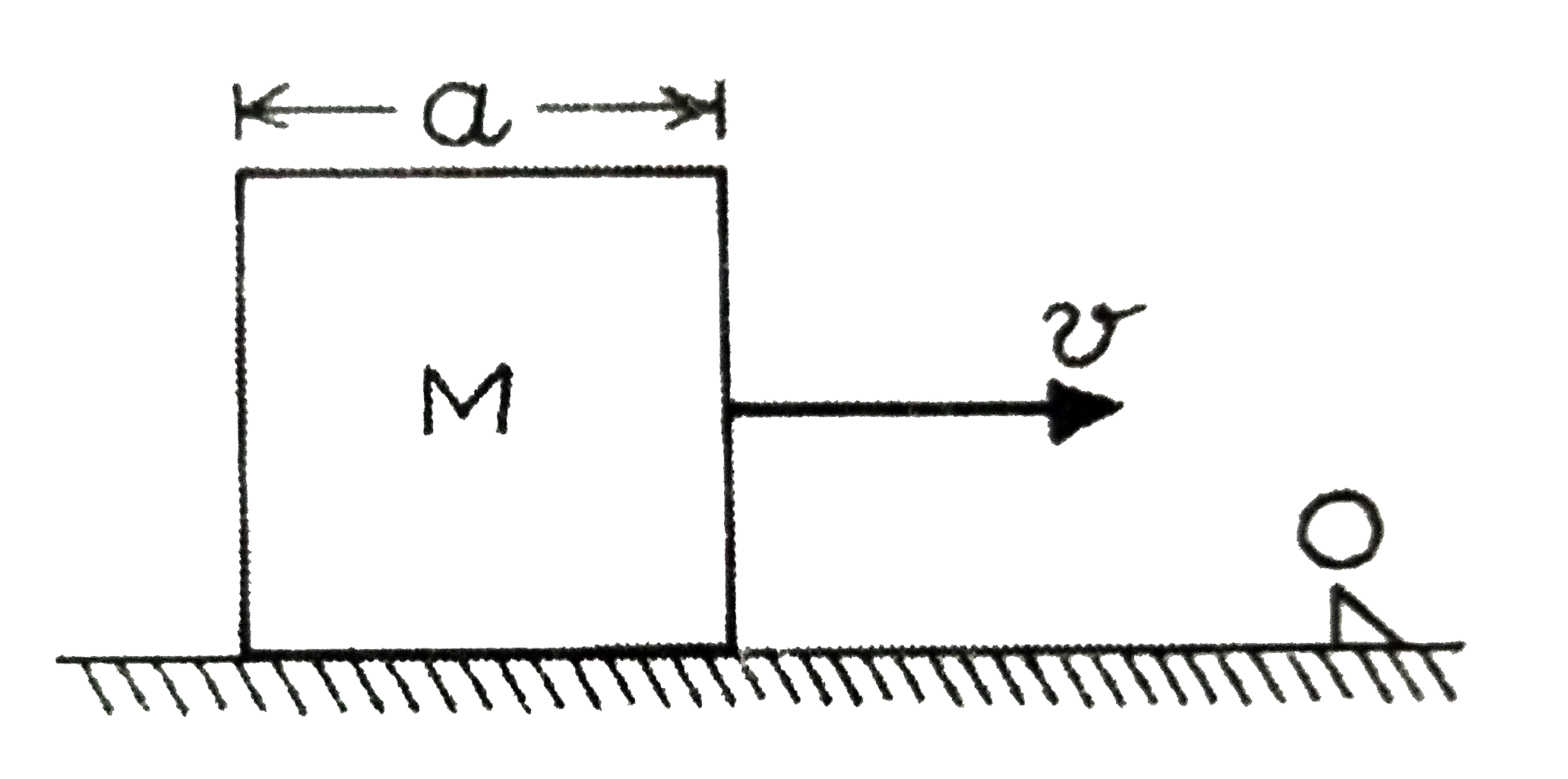
View Solutionभुजा a का एक घनाकार ब्लॉक एक चिकने क्षैतिज तल पर वेग `v` से चल रहा है। बिंदु `O` पर यह एक मेंड से टकराता है। टकराने के पश्चात ब्लॉक की कोणीय चाल है:
View Solutionघूर्णन करते हुए दो पिण्डों A तथा B के द्रव्यमान क्रमश: `m` तथा `2m` और जड़त्व आघूर्ण क्रमशः `I_(A)` तथा `I_(B)(I_(B)gtI_(A))` हैं। इन दोनों की घूर्णन गतिज ऊर्जायें परस्पर बराबर हैं। यदि कोणीय संवेग क्रमशः `J_(A)` और `J_(B)` हो तो
View Solutionकिसी बिंदु `vecr=2hati-6hatj-12hatk` पर एक बल `vecF=alpha hati+3hatj+6hatk` लग रहा है। तो `alpha` के किस मान के लिए मूल बिंदु के परितः कोणीय संवेग संरक्षित रहेगा?
View Solutionएक पतली एकसमान छड़ बिंदु `O` पर कीलकित है तथा क्षैतिज तल में एक समान कोणीय चाल `omega` से घूम रही है। `t=0` पर एक छोटा कीड़ा `O` से चलना प्रारम्भ करके `t=T` समय पर छड़ के अन्तिम सिरे पर पहुंच कर रूक जाता है। कीड़ा छड़ के सापेक्ष एकसमान चाल `v` से चलता है । निकाय की कोणीय चाल पूरे समय `omega` बनी रहती है। `O` के परितः निकाय पर लगने वाले बल आघूर्ण का मान `(tau)` समय के साथा जिस प्रकार बदलता है उसका सर्वोत्तम वर्णन किस ग्राफ में है?
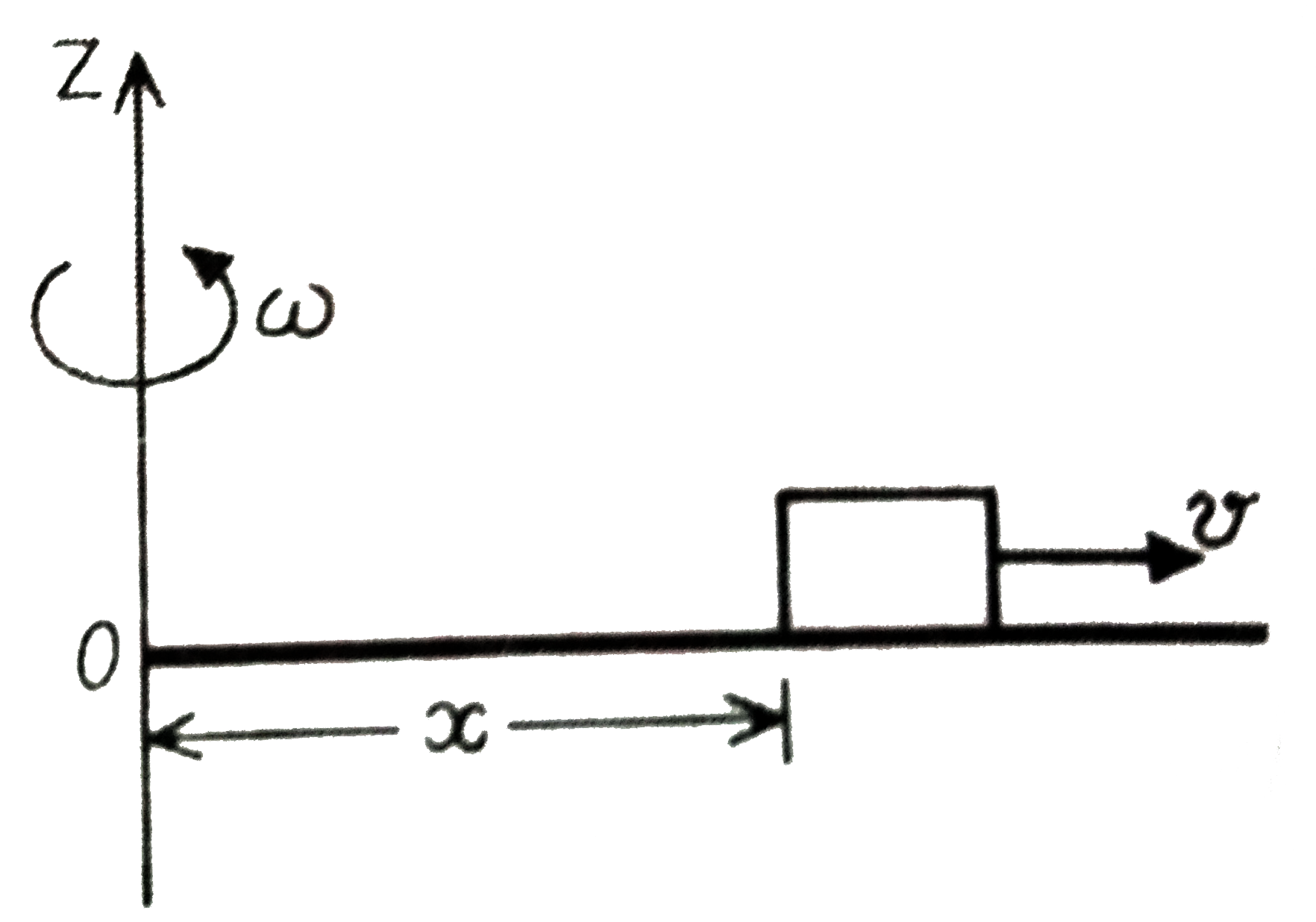
View Solutionलम्बाई `l` की एक अवितान्य डोरी से बंधे द्रव्यमान `m` के एक गोलाकार को एक ऊर्ध्वाधर आधार से लटकाया जाता है। गोलक ऊर्ध्वाधर के परितः कोणीय चाल `omega` रेडियन/सेकण्ड से एक क्षैतिज वृत्त में घूर्णन करता है। निलम्बन बिंदु पर
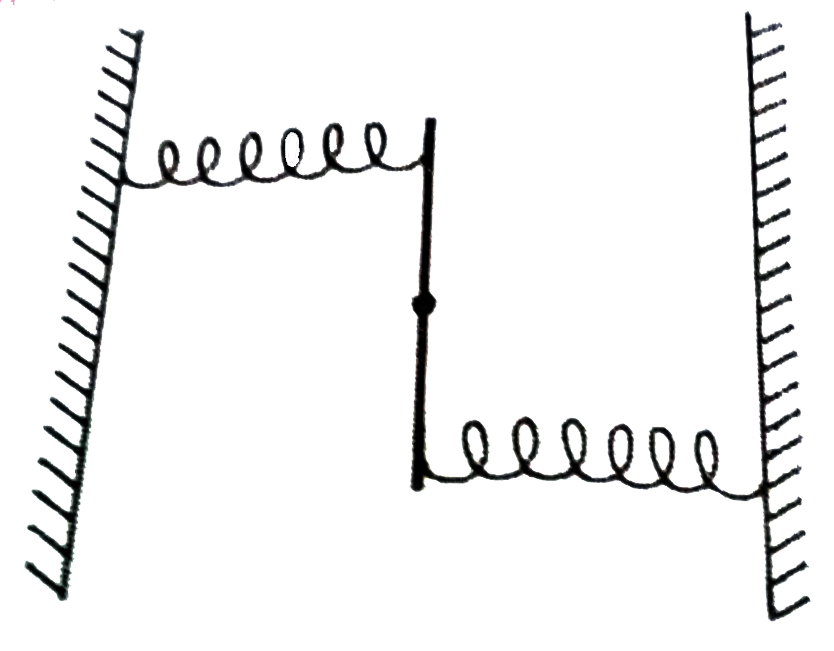
View Solutionलम्बाई `L` तथा द्रव्यमान `M` की एकसमान छड़ अपने केंद्र पर कीलकित है। इसके दोनों सिरों पर समान स्प्रिंग नियतांक `k` की दो स्प्रिंगें चित्रानुसार द़ढ़ आलम्बों से जुड़ी है। छड़ क्षैतिज तल में दोलन करने के लिए स्वतंत्र है। छड़ को एक दिशा में धीरे से अल्प कोण `theta` से धकेलकर छोड़ दिया जाता है। छड़ के दोलन की आवृत्ति है:
View Solutionकणों के एक द्रव्यमान पर लग रहे बाहरी बलों का परिणामी यदि शून्य हो तो किसी जड़त्वीय फ्रेम से यह निश्चित रूप से कहा जा सकता है।
View Solutionएक गेद घटती चाल से वृत्ताकार पथ के अनुदिश चलने के लिए प्रतिबन्धि त है। गेंद के लिए सही कथन चुनिएः
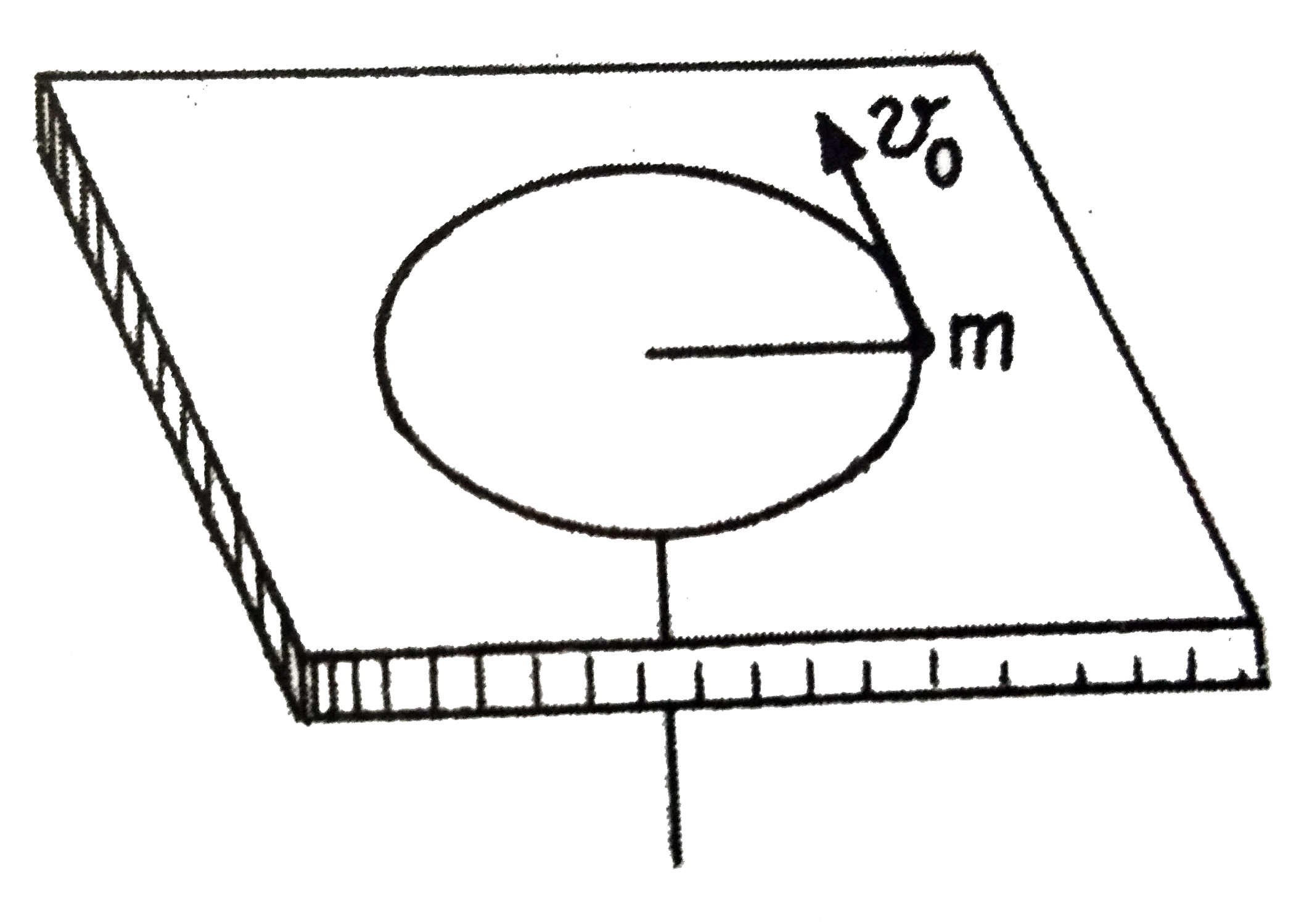
View Solutionv`m` द्रव्यमान का एक पिण्ड `R_(0)` त्रिज्या के पथ में किसी चिकनेक क्षैतिज सतमल पर `v_(0)` वेग से गति कर रहा है। यह पिण्ड एक डोरी से बंधा है यह डोरी समतल पर बने एक चिकने छिद्र से होकर गुजरती है जैसा कि आरेख में दर्शाया गया है। इस डोरी पर तनाव को धीरे-धीरे बढ़ाया जाता है जिससे अंत में यह पिण्ड `m,(R_(0))/2` त्रिज्या के वृत्ताकार पथ पर गति करने लगता है । गतिज ऊर्जा का अन्तिम मान है
View Solutionबर्फ पर चक्रण करती एक नर्तकी जब अपनी भुजायें मोड़ लेती है तो चक्रण की दर बढ़ जाती है । इसका कारण है:
View Solutionद्रव्यमान `M` तथा त्रिज्या `R` की एक डिस्क एक क्षैतिज तल पर कोणीय चाल `omega` से लुढ़क रही है। मूल बिंदु `O` के परितः डिस्क के कोणीय संवेग का परिमाण है:

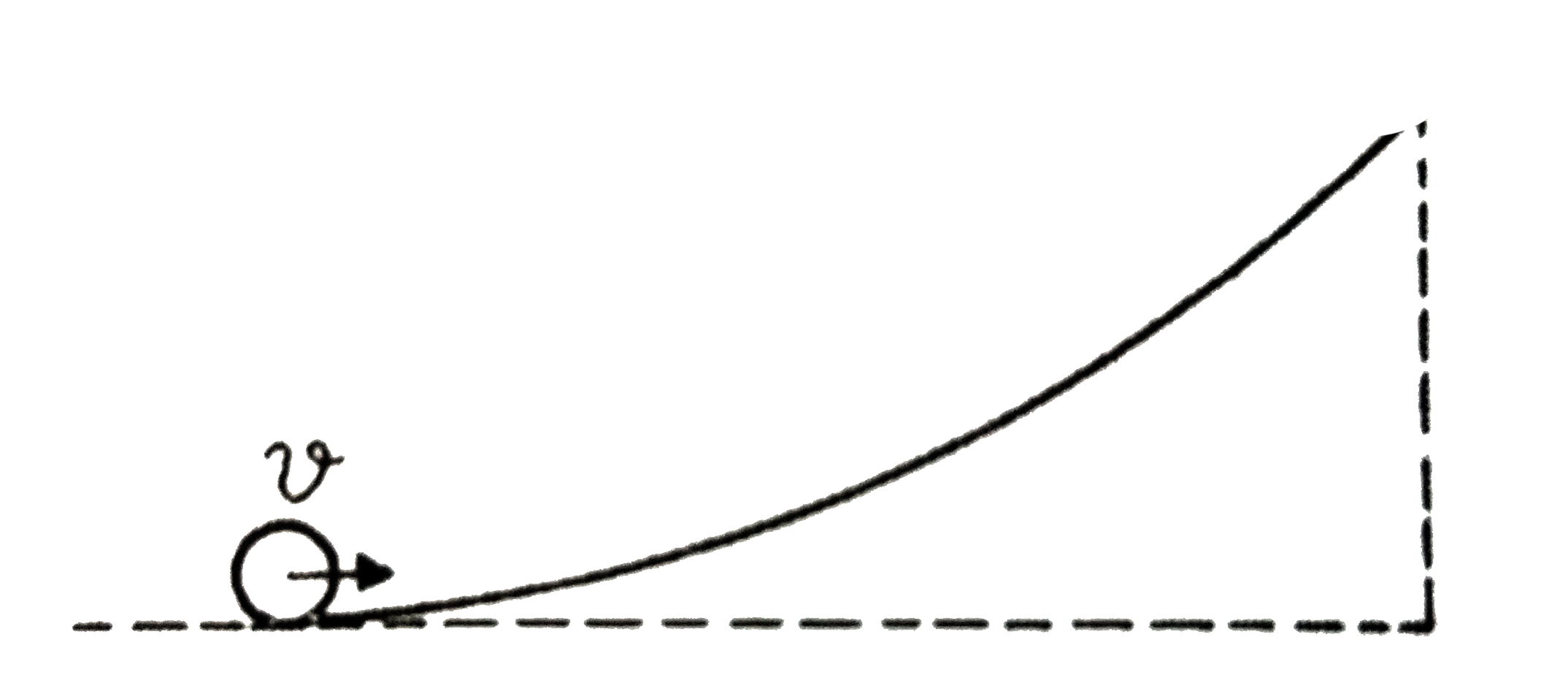
View Solutionत्रिज्या `r` तथा द्रव्यमान `m` का एक छल्ला एक खुरदरे क्षैतिज तल पर कोणीय वेग `omega_(0)` से घूम रहा है छल्ले के केंद्र का प्रारम्भिक वेग शून्य है। छल्ले के केंद्र का वेग क्या होगा जब यह फिसलता बंद हो जाये?`
View Solutionद्रव्यमान `M` तथा त्रिज्या `R` का एक छल्ला अपने केंद्र से होकर जाने वाली स्थिर ऊर्ध्वाधर अक्ष के परितः कोणीय वेग `omega` से घूम रहा है। इस क्षण `M//8` द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केंद्र `O` पर विराम स्थिति में है। वो दर्शाये चित्रानुसार छल्ले पर लगी द्रव्यमानहीन दो छड़ों पर त्रिज्यतः बाहर की ओर गति कर सकतेक हैं किसी क्षण पर निकाय की कोणीय गति `8/9 omega` है तथा बिंदु द्रव्यमान `O` से `3/5R` दूरी पर है। इस क्षण दूसरे बिंदु द्रव्यमान की `O` से दूरी होगी:
View Solutionदो डिस्कों (चक्रिकायों) के जड़त्व आघूर्ण आपस में बराबर हैं। ये अपनी-अवपी नियमित अक्ष जो इनके समतल के लम्बवत है और चक्रिका के केंद्र से होकर गुजरती है के परितः क्रमश: `omega_(1)` तथा `omega_(2)` कोणीय वेग से घूण्रन कर रही है। इनकों एक दूसरे के सम्मुख इस प्रकार सम्पर्क में लाया जाता कि इनकी घूर्णन अक्ष संपाती हो जाती है। तो इस प्रक्रम में ऊर्जा क्षय के लिए व्यंजक होगा:
View Solutionएक ठोस गोला लोटन गति में है। लोटन गति में वस्तु की स्थानान्तरीय गतिज ऊजा (`K_(t)`) के साथ-साथ घूर्णी गतिज ऊर्जा (`K_(r)`) भी होती है गोले के लिए `K_(t):K_(t)+R_(r))` का अनुपात होगा:
View Solutionलम्बाई `l`तथा द्रव्यमान `m` की एक पतली एकसमान छड़ इसके एक सिरे से गुजरने वाली क्षैतिज अक्ष के परितः मुक्त रूप से झूल रही है। इसकी अधिकतम कोणीय चाल `omega` है। इसका द्रव्यमान-केंद्र जिस महत्तम ऊंचाई तक उठता है वह है
View Solutionएक समान घनत्व वाली एक छाटी वस्तु प्रारम्भिक वेग `v` से एक वक्रीय पृष्ठ पर ऊपर की ओर का लुढ़कती है। यह अपनी प्रारम्भिक स्थिति के सापेक्ष `(3v^(2))/(4g)` की अधिकतम ऊँचाई तक पहुँचती है । वस्तु है:
View Solutionएक डिस्क तथा एक गोला जिनकी त्रिज्यायें समान परंतु द्रव्यमान भिन्न हैं समान उन्नतांश तथा लम्बाई के दो आनत तलों पर लुढ़कते है। दोनों पिण्डों में से तली पहले कौन पहुंचेगा?
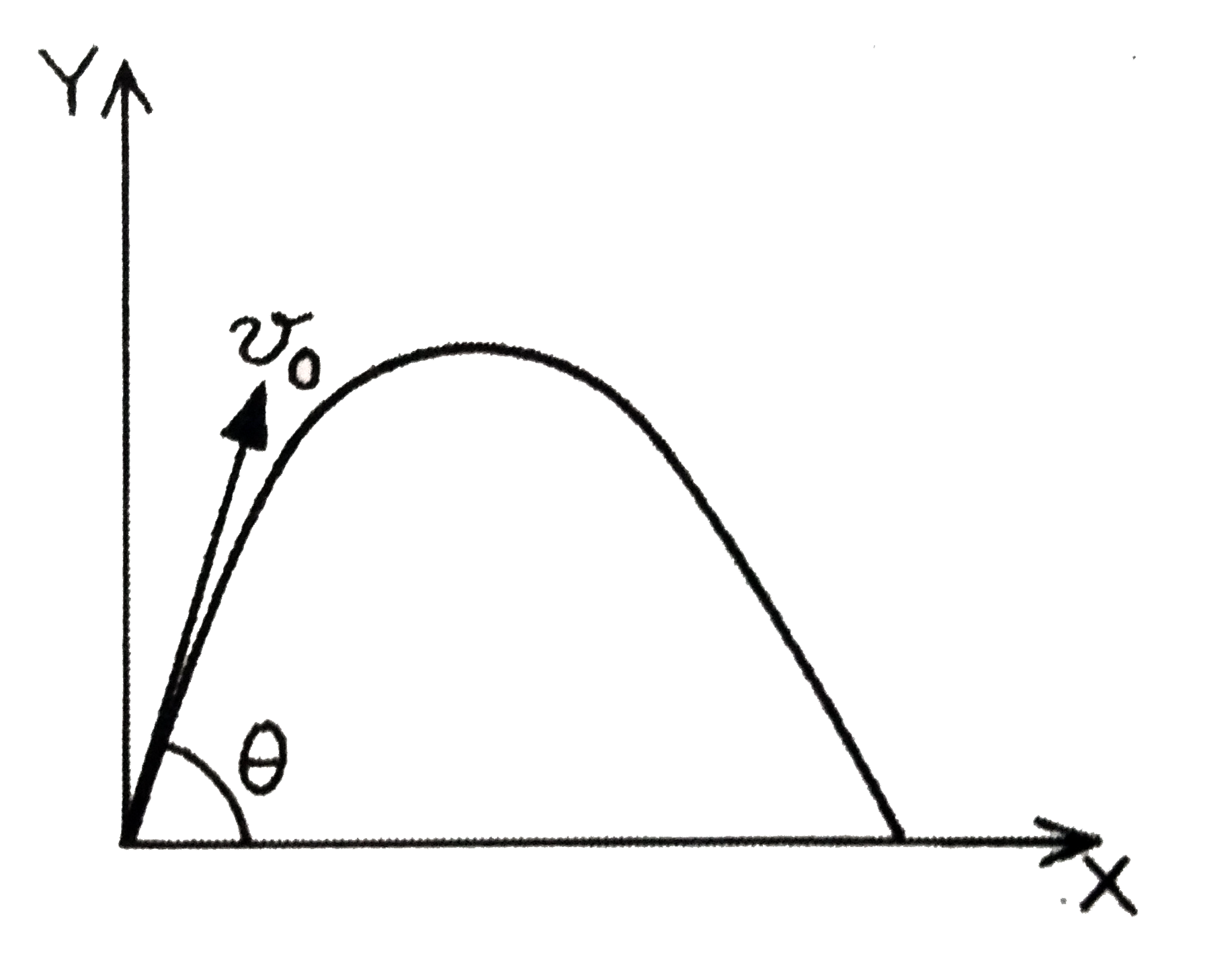
View Solution`m` द्रव्यमान का एक छोटा कण `X`अक्ष से `theta` कोण पर प्रारम्भिक वेग `v_(0)` से x-y तल में चित्रानुसार प्रक्षेपित किया गया है। समय `t lt (v_(0)sin theta)/g` पर कण का कोणीय संवेग है:
जहां `hati, hatj, hatk, x-, y-` तथा z- अक्ष के अनुदिश एकांक सदिश है।
View Solution1.6 किग्रा द्रव्यमान तथा `l` लम्बाई की एकसमान लकड़ी की एक डंडी एक चिकनी खड़ी दीवार, जिसकी ऊंचाई `h(ltl)` है पर आनत तरीके से इस तरह से रखी गयी है कि डंडी का एक छोआ सा भाग दीवार से ऊपर निकला हुआ है। डंडी दीवार के साथ `30^(@)` का कोण बना री है और डंडी का आधार एक घर्षण वाली जमीन पर है। दीवार से ड़डी पर प्रतिक्रिया तथा जमीन से डंडी पर प्रतिक्रिया की मात्रा समान है। `h//l` का अनुपात एवं डंडी के आधार पर घर्षण बल `f` है (`g=10m//sec^(2)`)
View Solutionएक त्रिज्या `R` तथा लम्बाई `l` के एकसमान बेलन का उसके अभिलम्ब द्विभाजक के सापेक्ष जड़त्व आघूर्ण `I` है। जड़त्व आघूर्ण के निम्नतम मान के लिए अनुपात `l//R` क्या होगा?
View Solutionकोई ठोस गोला मुक्त आकाश में अपनी सममिति अक्ष के परितः मुक्त रूप से घूर्णन कर रहा है। इस गोले का द्रव्यमान समान रखते हुए इसकी त्रिज्या में वृद्धि की जाती है। गोले के लिए निम्नलिखित में से कौन-सी भौतिक राशि स्थिर रहेगी?
View Solutionतीन पिण्ड A (एक ठोस गोला) B (एक पतली वृत्ताकार चकती) तथा C (एक वृत्ताकार छल्ला) जिनमें प्रत्येक का द्रव्यमान `M` तथा त्रिज्या `R` है समान कोणीय चाल `omega` से अपनी सममितित अक्षों के परितः चक्रण कर रहे हैं। इन्हें विरामावस्था में लाने के लिए किए जाने वाले आवश्यक कार्यों (`W`) के लिए कौन-सा संबंध सही है:
View Solution
विविध प्रतियोगी परीक्षाओं के लिए (वस्तुनिष्ट प्रकार के प्रश्न) questions and complete solutions for chapter दृढ़ पिण्डों की घूर्णन गति of NAGEEN PHYSICS (HINDI) of Class 11