Complete Solutions to वस्तुनिष्ठ प्रकार प्रश्न of chapter सरल आवर्त गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | सरल आवर्त गति |
| KUMAR MITTAL | वस्तुनिष्ठ प्रकार प्रश्न |
| Number Of Questions | 34 |
| Academic Year | 2023-24 |
एक कण का विस्थापन `x=0.2(cos^2""(pit)/2-sin^2"(pit)/2)` मीटर है कण की गति -
View Solutionदो सरल आवर्त गतियाँ दी गयी है `x_1=asinomegat+acosomegat` तथा `x_2=asinomegat+a/sqrt3cosomegat`, पहली व दूसरी गति के आयामों का अनुपात तथा उनके बीच कलांतर क्रमशः -
View Solutionदो विस्थापनों `y_1a sinomegat " तथा "y_2=bcosomegat ` के अध्यारोपण से परिणामी गति
View Solutionएक कण x=-A तथा x=+A के बीच सरल आवर्त गति कर रहा है यह 0 से `A//2` तक जाने में `T_1` समय लेता है तथा `A//2` से A तक जाने में `T_2` समय लेता है तब ,
View Solutionदो कण X-अक्ष के अनुदिस सामान आयाम A तथा आवर्ती `omega` से सरल आवर्त गति कर रहे है उनकी मध्य अवस्था के बीच दुरी `x_0,(x_0gtA)` है यदि उनके बीच अधिकतम दूरी `(x_0+A)` है तब उनकी गति में कालांतर है
View Solutionएक कण A आयाम से सरल आवर्त गति कर रहा है जब यह अपने मूल स्थान से `2A//3` पर पहुँचता है तब अचानक इसकी गति तिगुनी कर दी जाती है तब इसका नया आयाम है
View Solutionकिसी कण की रेखीय सरल आवर्त गति का आयाम 3 सेमी है जब यह कण अपनी मध्य स्थिति से 2 सेमी दूरी पर होती हैफ़ तो उस समय इसके वेग का परिमाण , इसके त्वरण के बराबर होता है इस कण का आवर्तकाल ( सेकण्ड में ) है
View Solutionएक कण एक सरल रेखा में सरल आवर्त गति से गतिमान है यह विरामवस्था से प्रारम्भ कर प्रथम `tau` सेकण्ड में दूरी a और `tau`सेकण्ड में दूरी 2a उसी दिशा में तय करता है तब
View Solutionसरल आवर्त गति करते हुए किसी कण का x -t आरेख दर्शाया गया है समय `t=4/3` सेकण्ड पर कण का त्वरण है ,
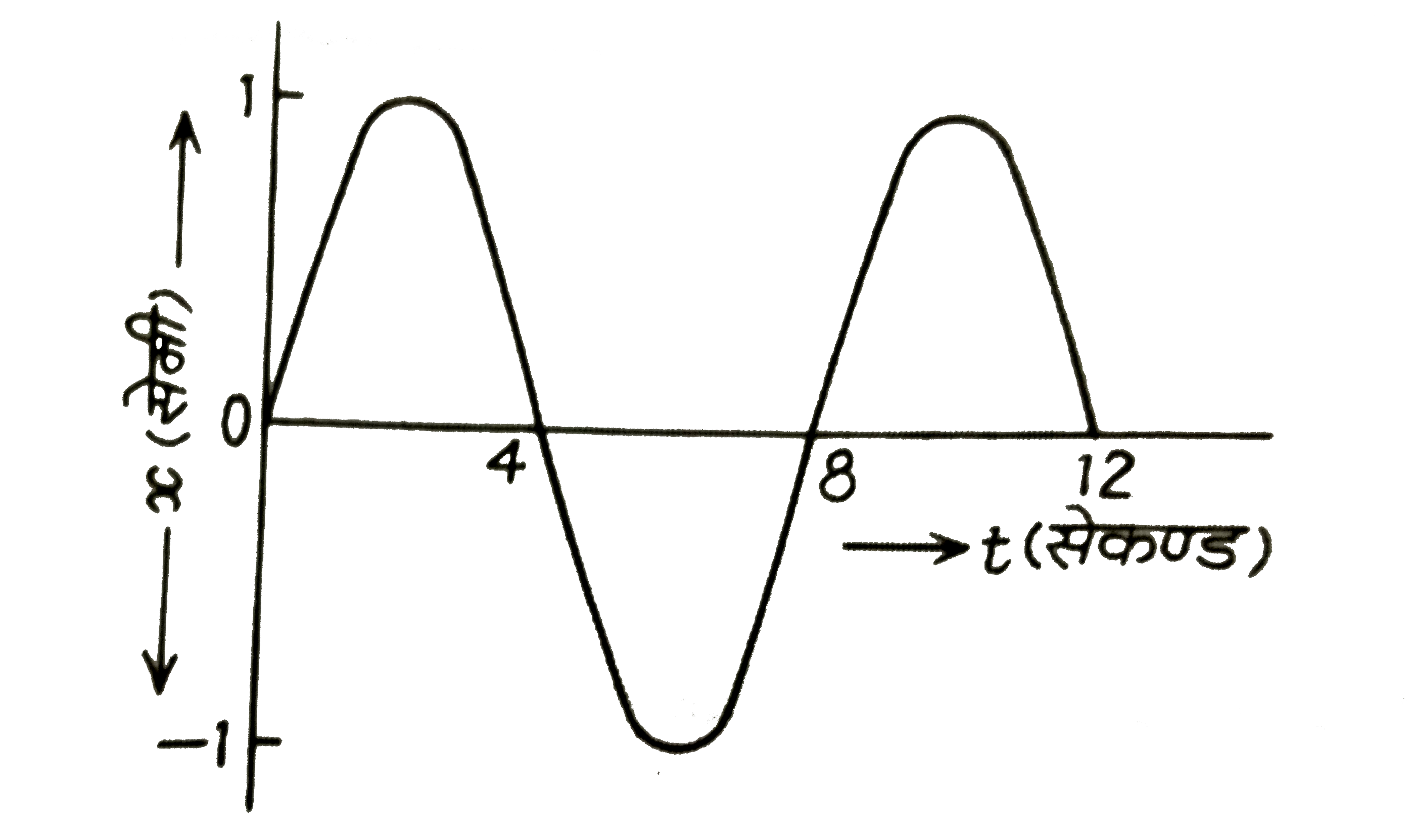
View Solutionसरल आवर्त गति करते हुए किसी कण का अधिकतम त्वरण `alpha` तथा `beta` अधिकतम वेग है तो इसके कम्पन्न का आवर्तकाल होगा
View Solutionकिसी पिण्ड ( वस्तु ) के चिकने क्षैतिज पृष्ठ पर दोलनों के समीकरण को `x=A cos (omegat)` द्वारा निरूपित किआ जाता है जहाँ x=t समय पर विस्थापन, `omega` दोलनों की आवृति तो t के साथ a विचरण ( परिवर्तन ) को कौन-सा ग्राफ सही रूप में दर्शाता है
यहाँ a = समय t पर त्वरण, T=आवर्तकाल
View Solutionकोई लोलक एक काफी ऊँचे भवन की छत से लटका है और सरल आवर्त लोलक की भाँति मुक्त रूप से आगे-पीछे गति कर रहा है। माध्य स्थिति से 5 मीटर की दुरी पर इसके गोलक का त्वरण 20 मीटर / सेकण्ड`""^2` है दोलन का आवर्तकाल है -
View Solutionएक सरल लोलक का आवर्तकाल `T_1` है जब इसके निलंबन-बिंदु को ऊर्ध्वाधर ऊपर की ओर `y=kt^2` के अनुशार चलाया जाता है , जहाँ y ऊर्ध्वाधर चली गई दूरी है तथा k = 1 मीटर/सेकण्ड`"^2` है तब इसका आवर्तकाल हो `T_2` जाता है `T_1^2//T_2^2` का मान है
( g=10 मीटर/सेकण्ड`"^2`)
View Solutionएक आदर्श स्प्रिंग , जिसका स्प्रिंग-नियतांक k है , छत से लटकाई गई है तथा उसके निचले सिरे से द्रव्यमान M के ब्लॉक को बांधा गया है यदि ब्लॉक को स्प्रिंग की अतानित अवस्था से छोड़ा जाये , तो स्प्रिंग में 'अधिकतम' विस्तारण का मान है -
View Solutionदो अतानित स्प्रिन्गे `S_1` तथा `S_2` जिनके स्प्रिंग - नियतांक क्रमशः k तथा 4k है को एक ब्लॉक B से जोड़ा गया है ( चित्र ) स्प्रिंगों के दूसरे सिरों को आधार `M_1` तथा `M_2` से जोड़ा गया है , जो दीवार से नहीं जुड़े है स्प्रिंगों तथा आधारों का द्रव्यमान नगण्य है कहीं भी कोई घर्षण नहीं है ब्लॉक B को दीवार -1 की ओर एक अलप - दूरी x तक विस्थापित करके छोड़ दिए जाता है ब्लॉक वापस आता है तथा दीवार -2 की ओर अधिकतम दूरी y तक जाता है x तथा y को ब्लॉक की साम्यावस्था से मापा जाता है अनुपात `y//x` का मान है
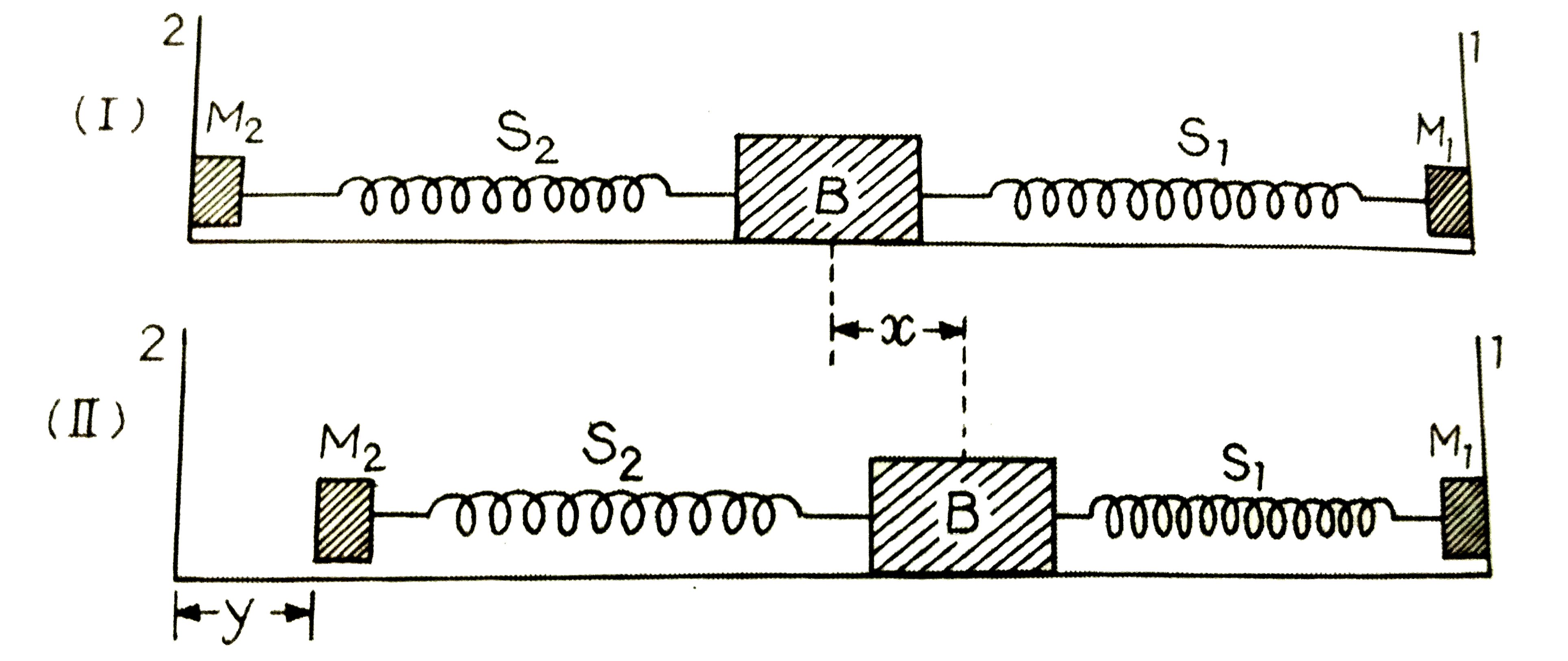
View Solutionयदि किसी सरल रेखा के अनुदिश सरल आवर्त गति करते हुए किसी कण की मूलबिंदु से दूरी `x_1` तथा `x_2` होने पर , उसके वेग क्रमशः `v_1` तथा `v_2` है तो इस कण का आवर्तकाल है
View Solutionm द्रव्यमान का एक गुटका P घर्षणहीन ताल पर रखा गया है उसी द्रव्यमान का एक अन्य गुटका Q , गुटके P पर रखा गया गया है Q को एक द्रव्यमान स्प्रिंग से , जिसका स्प्रिंग-नियतांक k है, एक दीवार से बांधा गया है दोनों गुटको के बीच स्थैतिज घर्षण गुणांक `mu_s` है स्प्रिंग को दूरी A से खींचने के लिए , गुटको P तथा Q को साथ-साथ चलाया जाता है छोड़ने पर , गुटके बिना फिसले दोलन करते है गुटको P व Q के बीच अधिकतम घर्षण-बल है ,

View Solutionचित्र में प्रदर्शित द्रव्यमान m सरल आवर्त गति कर रहा है इसका आयाम A है बिंदु P का आयाम का होगा

View Solutionलकड़ी का के गुटका घर्षणहीन तल पर आवर्ती f से सरल आवर्त गति कर रहा है गुटके के पृष्ठ पर आवेश +Q है अब यदि गुटके पर एकसमान वैधुत क्षेत्र `vecE` लगाया जाये , तो गुटके की सरल आवर्त क्या होगी
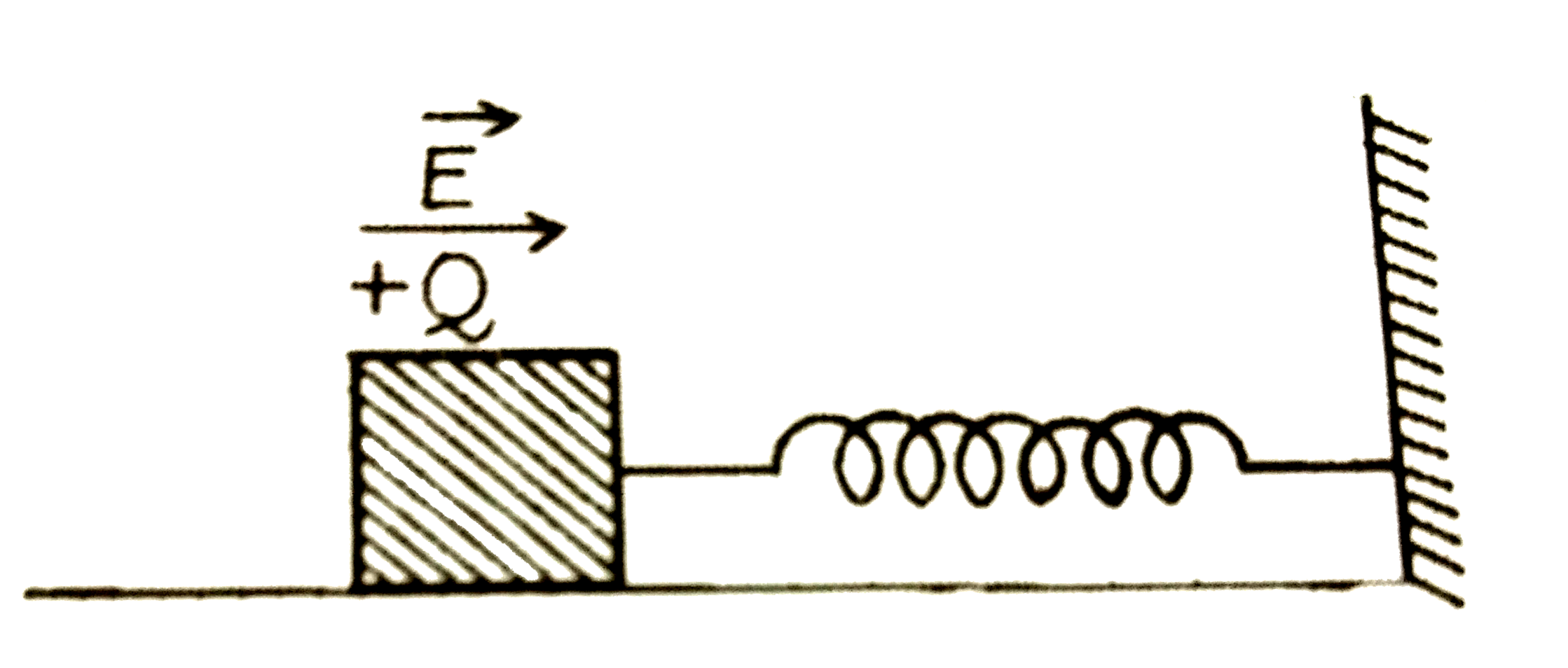
View Solutionकिसी ठोस में चंडी का एक परमाणु `10^(12)//sec` की आवृति से किसी दिशा में सरल आवर्त गति करता है एक परमाणु को दूसरे परमाणु से जोड़ने वाले बन्ध का बल नियतांक कितना होगा ( चांदी का आण्विक भार = 108 और आवोग्रादो संख्या= `6.02 xx 10^(23) "gm mole"^(-1)`)
View Solutionएक स्प्रिंग के निचले सिरे से m द्रव्यमान का पिण्ड लटका है जिसका ऊपरी सिरा स्थिर है स्प्रिंग का अपना द्रव्यमान नगण्य है जब द्रव्यमान m को थोड़ा खींचकर छोड़ देते है तो यह 3 सेकण्ड के आवर्तकाल से दोलन करने लगता है जब द्रव्यमान m के मान को 1 किग्रा बढ़ा दिया जाता है तो दोलनों का आवर्तकाल 5 सेकण्ड हो जाता है m का मान किग्रा में है
View Solutionदो गुटको A तथा B के द्रव्यमान , क्रमशः 3m तथा m है ये आपस में एक द्रव्यमानहीन , अवितान्य डोरी से जुड़े है इस पूरे निकाय को , आरेख में दर्शाये गए एक द्रव्यमानरहित स्प्रिंग द्वारा लटकाया गया है डोरी को काट देने के तुरंत पश्चात A और B के त्वरण के परिणाम होंगे क्रमशः
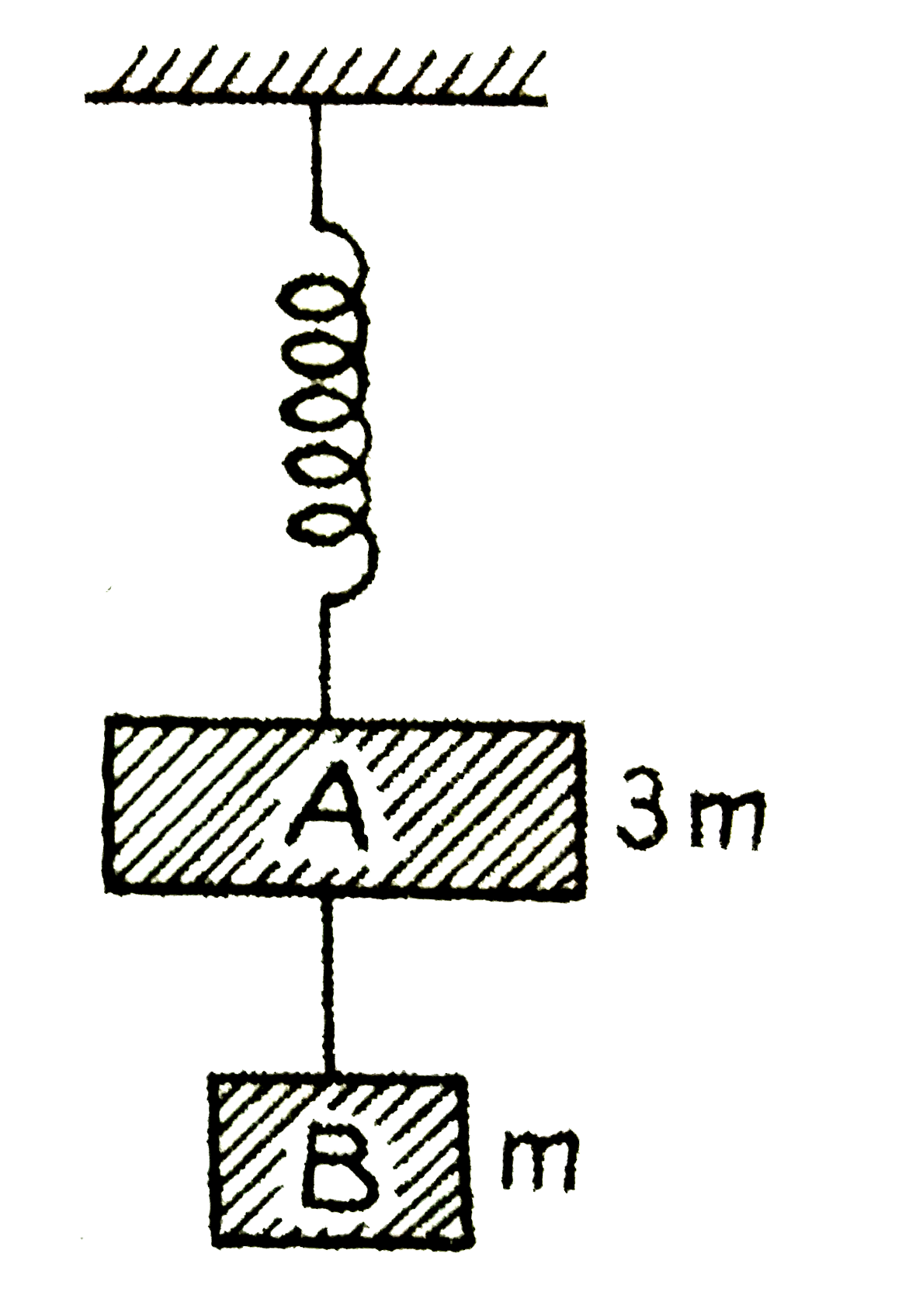
View Solutionबल-नियतांक k के एक स्प्रिंग को दो भागो में इस प्रकार काटा जाता है कि एक भाग की लम्बाई दूसरे से दोगुनी है लम्बे भाग का बल-नियतांक होगा -
View Solutionएक स्प्रिंग का स्प्रिंग नियतांक k है इसको तीन भागो में काट दिए गया है जिनकी लम्बाईयाँ का अनुपात 1:2:3 है इन तीन भागो को श्रेणी क्रम में जोड़ने पर , संयोजन का कमानी स्थिरांक k' तथा समान्तर क्रम में जोड़ने पर k'' है तो अनुपात k' : k'' होगा
View Solutionबराबर द्रव्यमान कि दो पिण्ड M तथा N दो द्रव्यमानहीन स्प्रिंगों से अलग-अलग लटके है स्प्रिंगों कि बल नियतांक क्रमशः `k_1` व `k_2` है यदि दोनों पिण्ड ऊर्ध्वाधर तल में इस प्रकार कम्पन्न करते है कि उनके अधिकतम वेग बराबर है , तब M कि कम्पन्न कि आयाम का N कि साथ अनुपात है
View Solutionएक द्रव्यमान M एक हलकी स्प्रिंग से लटका है एक अतिरिक्त द्रव्यमान m रखने पर स्प्रिंग x दुरी और खींच जाता है स्प्रिंग से लटके संयुक्त द्रव्यमानो का आवर्तकाल T होगा
View Solutionएक एकसमान बेलन जिसकी लम्बाई L , द्रव्यमान M तथा परिच्छेद क्षेत्रफल A है एक द्रव्यमानहीन स्प्रिंग द्वारा एक स्थिर बिंदु से ऊर्ध्वाधर लटका है यह संतुलन स्थिति में घनत्व p के द्रव में आधा डूबा है जब बेलन को थोड़ा नीचे खींच कर छोड़ दिए जाता है तो वह छोटे आयाम के साथ ऊर्ध्वाधर दोलन करने लगता है यदि स्प्रिंग का बल-नियतांक k हो , तो बेलन की आवृति है
View Solutionएक तार के टुकड़े को परवलय `y=kx^2` (Y-अक्ष ऊर्ध्वाधर ) आकर में मोड़ा गया है तार में m द्रव्यमान का एक मनका पड़ा है जो तार पर बिना घर्षण सरक सकता है तार की स्थिर अवस्था में यह मनका परवलय के निम्नतम बिंदु पर रहता है अब तार को एकसमान त्वरण a से X- अक्ष के समान्तर चलाया जाता है मनके की नई साम्यावस्था में , जहाँ वह तार की अपेक्षा स्थिर अवस्था में रह सकता है Y-अक्ष से दूरी होगी
View Solutionकिसी सरल लोलक के लिए , उसके विस्थापन d तथा उसकी गतिज ऊर्जा के बीच और विस्थापन d तथा उसकी स्थितिज ऊर्जा के बीच ग्राफ खींचे गए है निम्नांकित में से कौन-सा ग्राफ ( आलेख ) सही है (यहाँ ग्राफ केवल व्यवस्था आरेख है और स्केल के अनुशार नहीं है )
View Solutionएक कण आवर्तकाल T से सरल आवर्त गति कर रहा है समय t=0 पर वह साम्यावस्था की स्थिति में है अग्रांकित में से कौन सा ग्राफ समय के साथ गतिज ऊर्जा को सही दर्शाता है
View Solutionएक कण आवृति f से सरल आवर्त गति करता है इसकी गतिज ऊर्जा के दोलन की आवृति है
View Solutionm द्रव्यमान का एक कण X-अक्ष पर मूलबिंदु के परितः दोलन कर रहा है इसकी स्थितिज ऊर्जा `U(x)=k|x|^3` है जहाँ K एक धन नियतांक है यदि दोलन का आयाम a है तब इसका आवर्तकाल T :
View Solutionअक्ष के अनुदिस गति करने के लिए स्वतंत्र कण की स्थितिज ऊर्जा सीमाओं `-oolexleoo` के अंतर्गत `U(x)=k[1-e^(-x^2]]` द्वारा दी जाती है जहाँ k उपयुक्त विमाओ वाला धन-नियतांक है तब
View Solutionएक क्षैतिज स्प्रिंग से बंधा एक द्रव्यमान M आयाम `A_1` से सरल आवर्त गति कर रहा है जब द्रव्यमान M अपनी मध्य स्थिति से गुजरता है , तब इसके ऊपर एक छोटा द्रव्यमान m रख दिया जाता है अब दोनों आयाम `A_2` से गति करते है `(A_1//A_2)` का अनुपात है
View Solution
वस्तुनिष्ठ प्रकार प्रश्न questions and complete solutions for chapter सरल आवर्त गति of NAGEEN PHYSICS (HINDI) of Class 11