Complete Solutions to III. Multiple Choice Questions of chapter STATES OF MATTER : GASES AND LIQUIDES of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | STATES OF MATTER : GASES AND LIQUIDES |
| PRADEEP | III. Multiple Choice Questions |
| Number Of Questions | 7 |
| Academic Year | 2023-24 |
Real gases show deviations from ideal behaviour. Consequently, the observed molar volume of a gas is found to be different from theoretically calculated volume from ideal gas equation. The extent of deviation is measured in terms of compressibility factor, Z. It is found that gases which can be liquefied easily show largerdeviation. Further, it is found that higher the speed of the gas molecules, less are the deviations. However, for evergy gas, there is a particular temperature above which they show ideal bahaviour over an appreciable range of pressure. This temperature is called Boyletemperature. The plots of compressibility factor versus pressure for a few gases and for the same gas at different temperatures and for the same gas at different temperatures are given below in Figs (a) and (b) respectively.The ideal gas equation has, therefore, been modified and for real gases, we apply vab der Waals equation, `(P+(a)/(V_(2)))(V-b)=RT` for 1 mole of the gas.
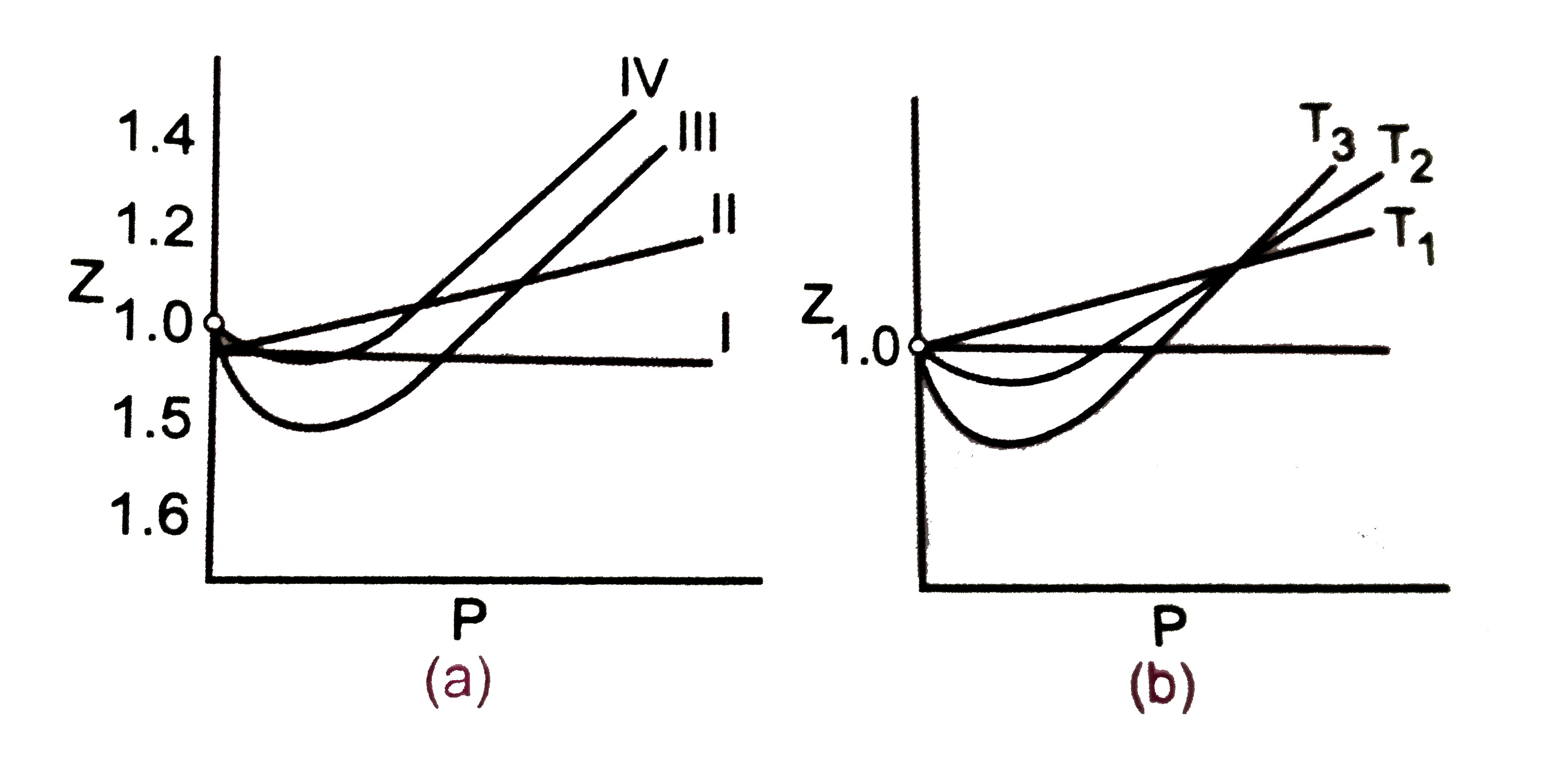
If `V_(0)` is the observed volume of a gas and `V_(i)` is the ideal gas or volume, then the compressibility factor (Z) for the gas is
View SolutionReal gases show deviations from ideal behaviour. Consequently, the observed molar volume of a gas is found to be different from theoretically calculated volume from ideal gas equation. The extent of deviation is measured in terms of compressibility factor, Z. It is found that gases which can be liquefied easily show largerdeviation. Further, it is found that higher the speed of the gas molecules, less are the deviations. However, for evergy gas, there is a particular temperature above which they show ideal bahaviour over an appreciable range of pressure. This temperature is called Boyletemperature. The plots of compressibility factor versus pressure for a few gases and for the same gas at different temperatures and for the same gas at different temperatures are given below in Figs (a) and (b) respectively.The ideal gas equation has, therefore, been modified and for real gases, we apply vab der Waals equation, `(P+(a)/(V_(2)))(V-b)=RT` for 1 mole of the gas.
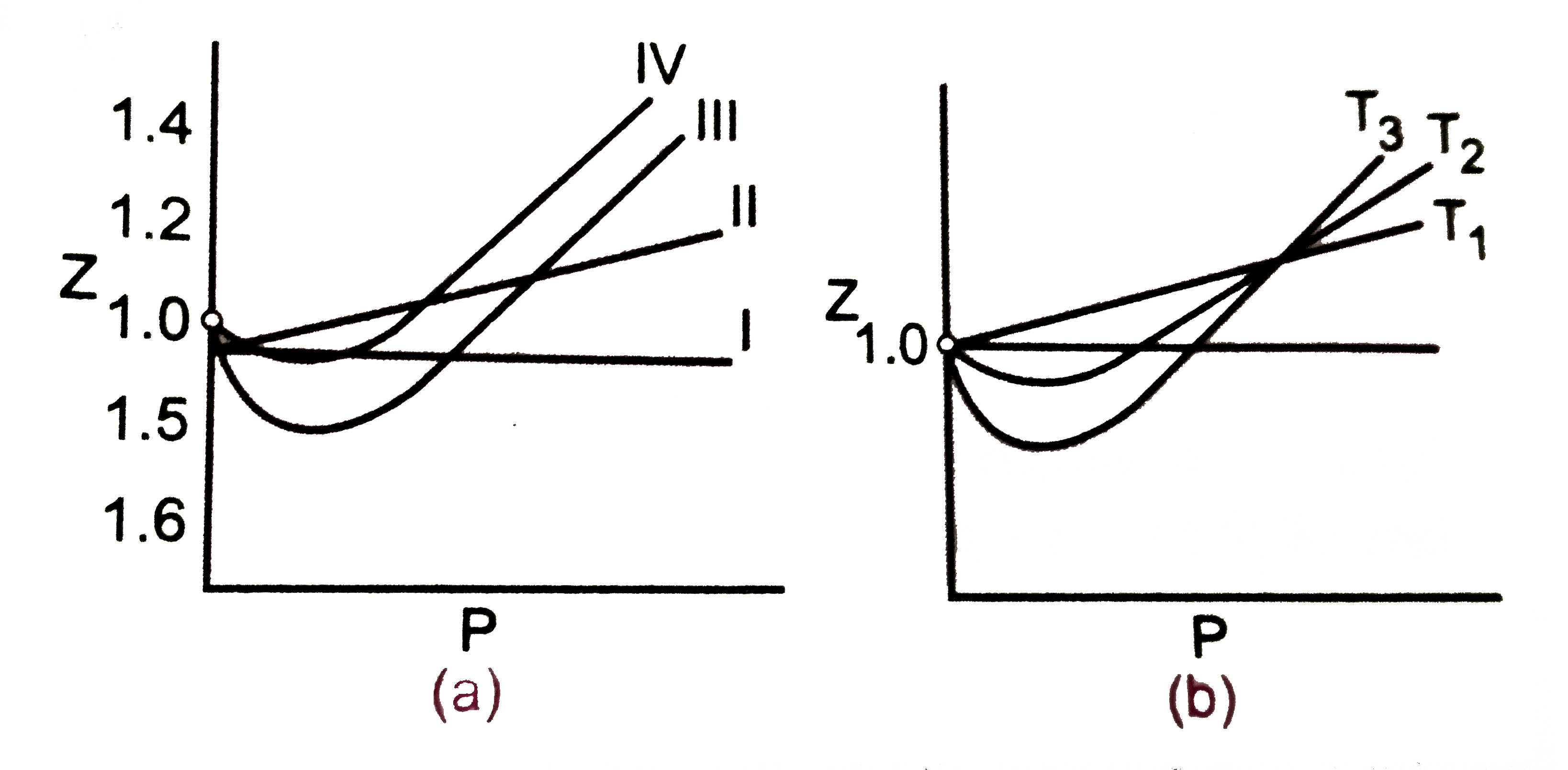
View SolutionReal gases show deviations from ideal behaviour. Consequently, the observed molar volume of a gas is found to be different from theoretically calculated volume from ideal gas equation. The extent of deviation is measured in terms of compressibility factor, Z. It is found that gases which can be liquefied easily show largerdeviation. Further, it is found that higher the speed of the gas molecules, less are the deviations. However, for evergy gas, there is a particular temperature above which they show ideal bahaviour over an appreciable range of pressure. This temperature is called Boyletemperature. The plots of compressibility factor versus pressure for a few gases and for the same gas at different temperatures and for the same gas at different temperatures are given below in Figs (a) and (b) respectively.The ideal gas equation has, therefore, been modified and for real gases, we apply vab der Waals equation, `(P+(a)/(V_(2)))(V-b)=RT` for 1 mole of the gas.
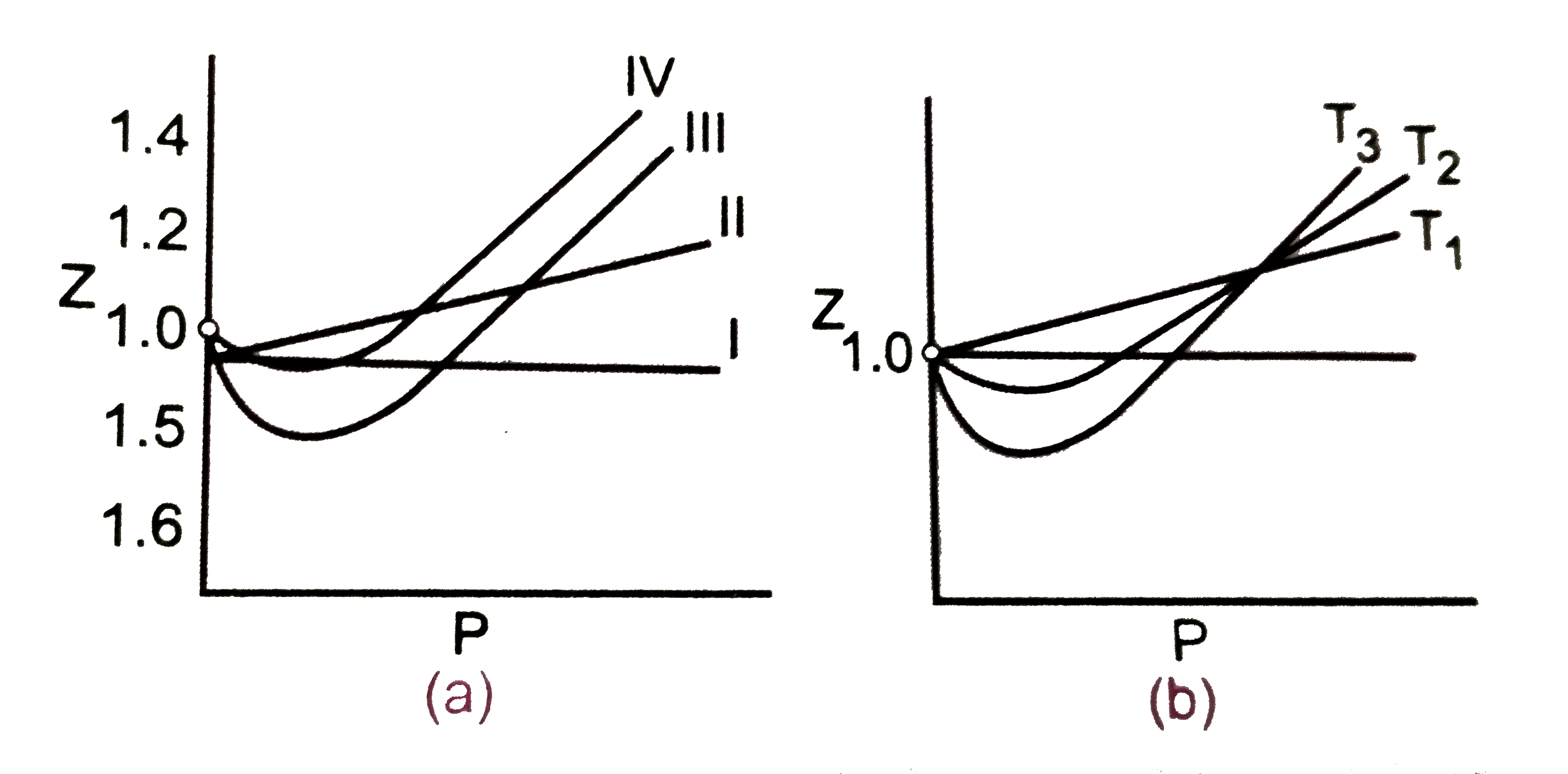
View SolutionReal gases show deviations from ideal behaviour. Consequently, the observed molar volume of a gas is found to be different from theoretically calculated volume from ideal gas equation. The extent of deviation is measured in terms of compressibility factor, Z. It is found that gases which can be liquefied easily show largerdeviation. Further, it is found that higher the speed of the gas molecules, less are the deviations. However, for evergy gas, there is a particular temperature above which they show ideal bahaviour over an appreciable range of pressure. This temperature is called Boyletemperature. The plots of compressibility factor versus pressure for a few gases and for the same gas at different temperatures and for the same gas at different temperatures are given below in Figs (a) and (b) respectively.The ideal gas equation has, therefore, been modified and for real gases, we apply vab der Waals equation, `(P+(a)/(V_(2)))(V-b)=RT` for 1 mole of the gas.
For 1 mole of gas II, the van der Waals equation reduces to the form
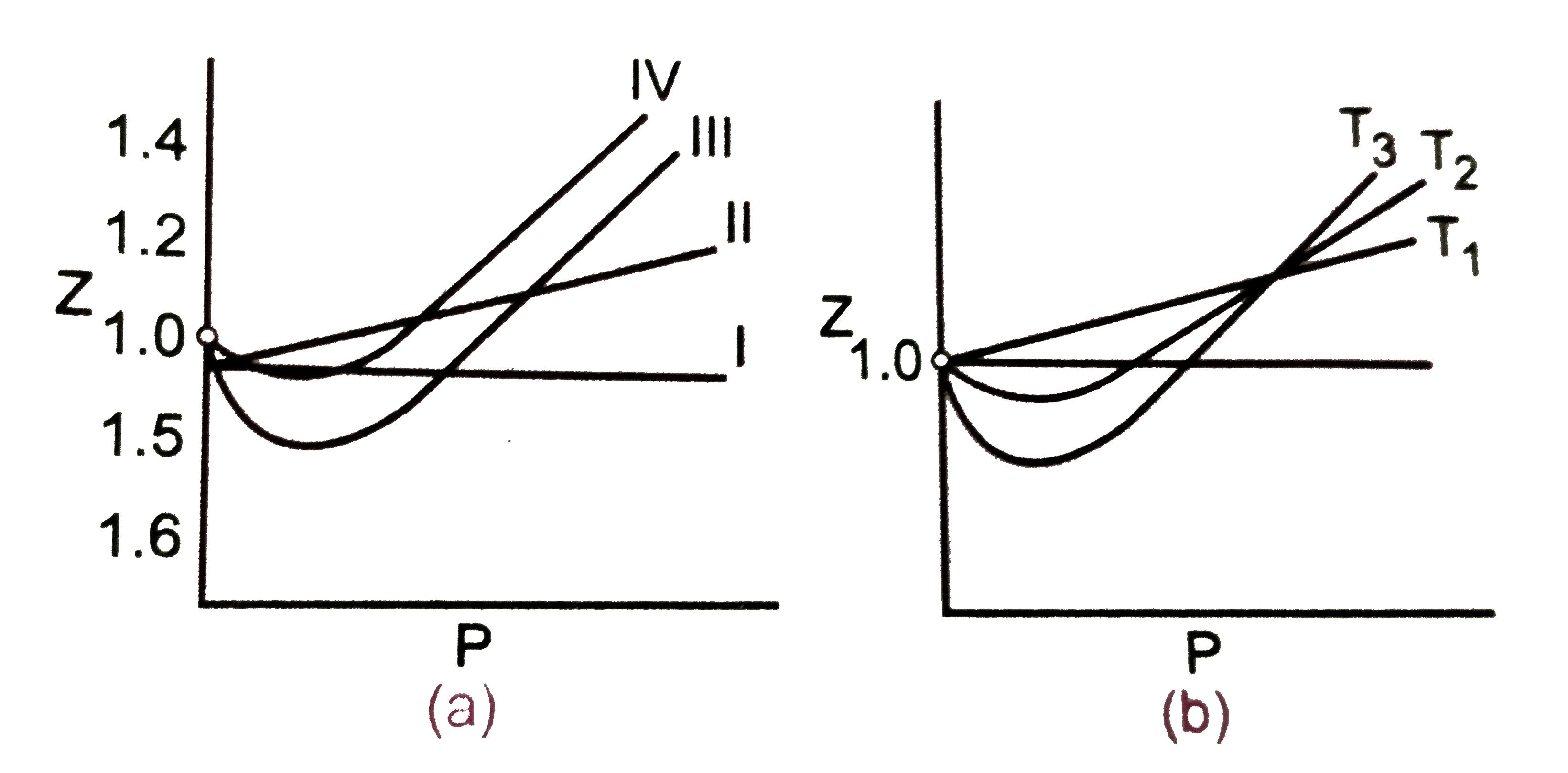
View SolutionReal gases show deviations from ideal behaviour. Consequently, the observed molar volume of a gas is found to be different from theoretically calculated volume from ideal gas equation. The extent of deviation is measured in terms of compressibility factor, Z. It is found that gases which can be liquefied easily show largerdeviation. Further, it is found that higher the speed of the gas molecules, less are the deviations. However, for evergy gas, there is a particular temperature above which they show ideal bahaviour over an appreciable range of pressure. This temperature is called Boyletemperature. The plots of compressibility factor versus pressure for a few gases and for the same gas at different temperatures and for the same gas at different temperatures are given below in Figs (a) and (b) respectively.The ideal gas equation has, therefore, been modified and for real gases, we apply vab der Waals equation, `(P+(a)/(V_(2)))(V-b)=RT` for 1 mole of the gas.
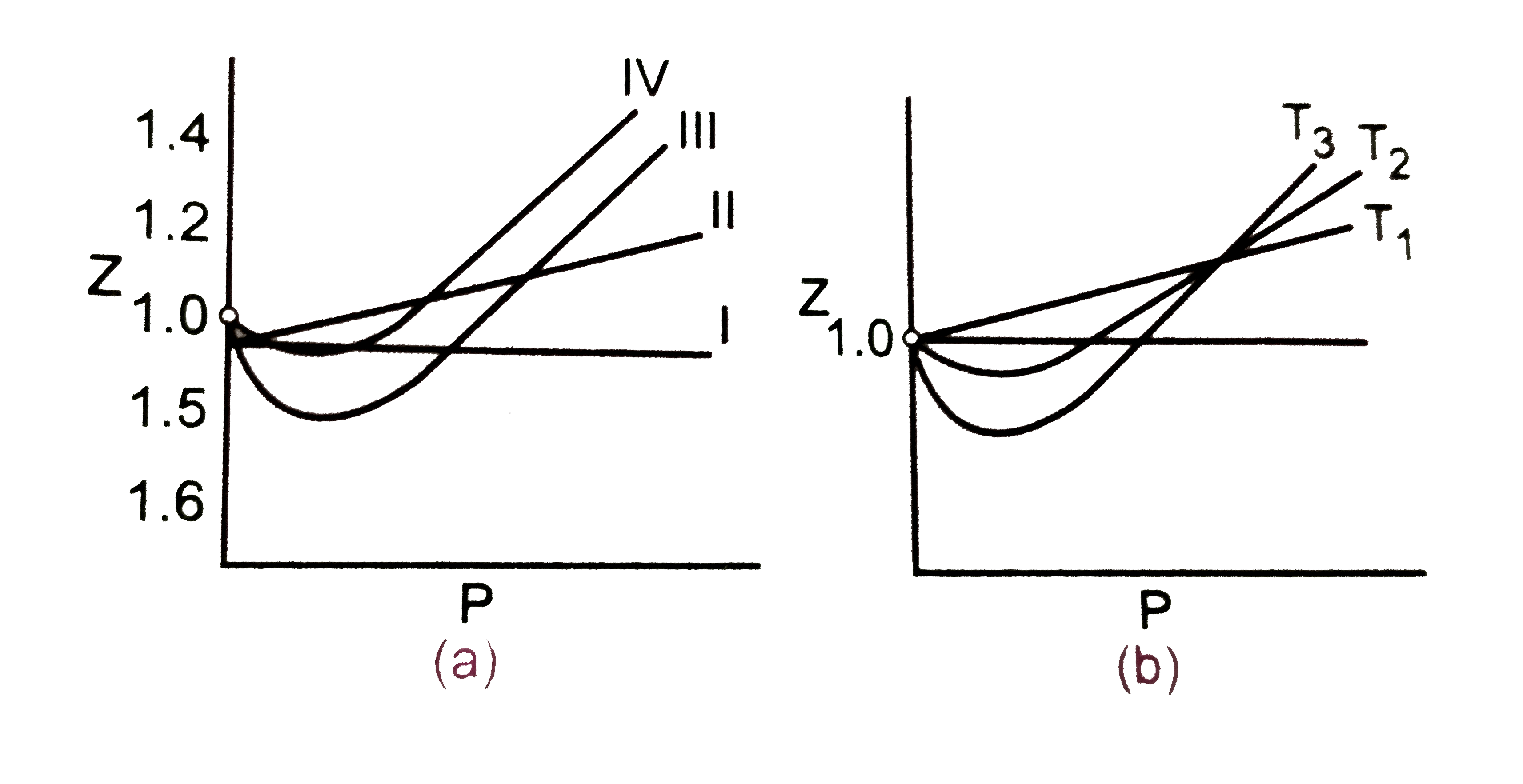
The gas which can be liquefied most easily is
View Solution(JEE Adavanced 2014)
X and Y are two volatile liquids with molecular weights 10 g `mol^(-1)` and 40 g `mol^(1)` respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube with length L=24 cn as shown in the figure. The tube is filled with an inert gas at 1 atmosphere pressure and a temperature of 300 K. Vapours of X and Y react to form a product which is first observed at a distance of d cm from the plug soaked in X. Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and the two vapours.
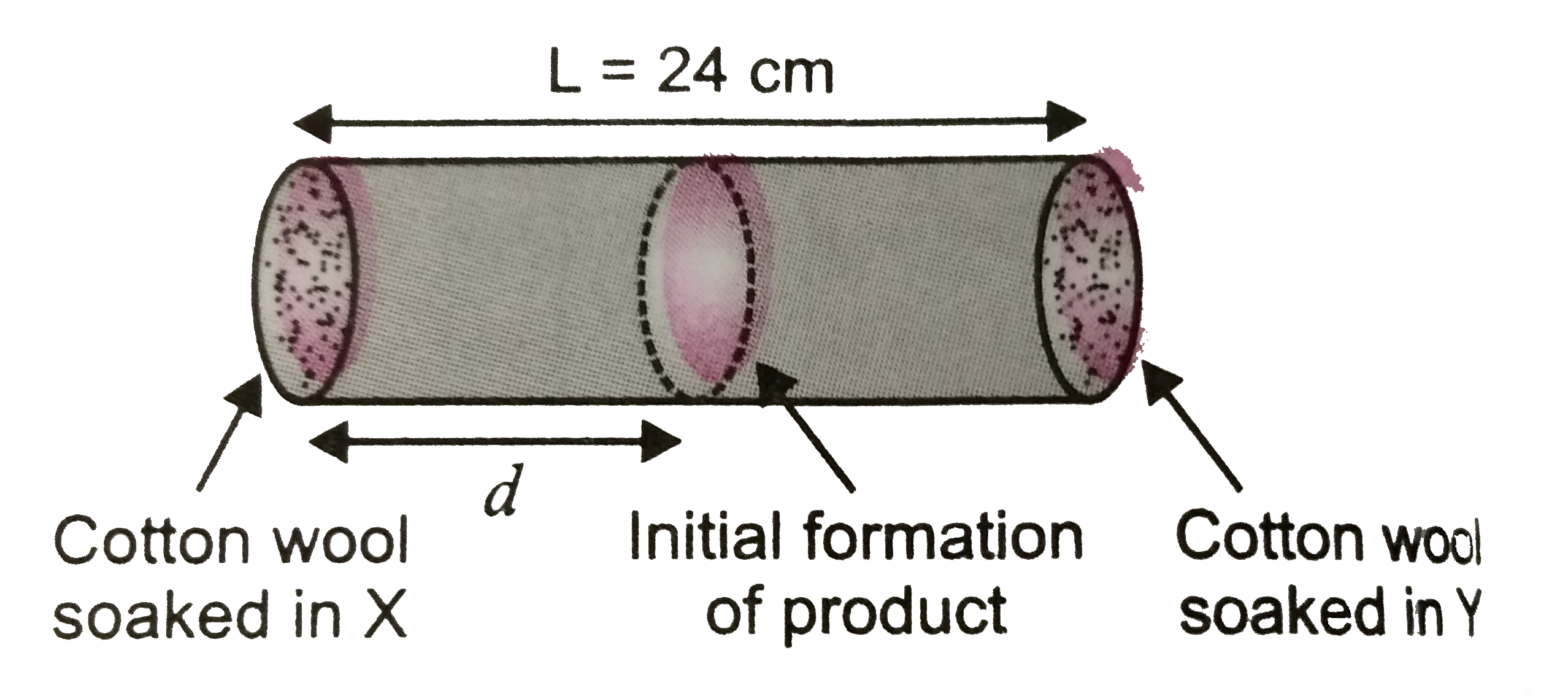
The value of d in cm (shown in the figure), as estimated from Graham's law, is
View Solution(JEE Adavanced 2014)
X and Y are two volatile liquids with molecular weights 10 g `mol^(-1)` and 40 g `mol^(1)` respectively. Two cotton plugs, one soaked in X and the other soaked in Y, are simultaneously placed at the ends of a tube with length L=24 cn as shown in the figure. The tube is filled with an inert gas at 1 atmosphere pressure and a temperature of 300 K. Vapours of X and Y react to form a product which is first observed at a distance of d cm from the plug soaked in X. Take X and Y to have equal molecular diameters and assume ideal behaviour for the inert gas and the two vapours.
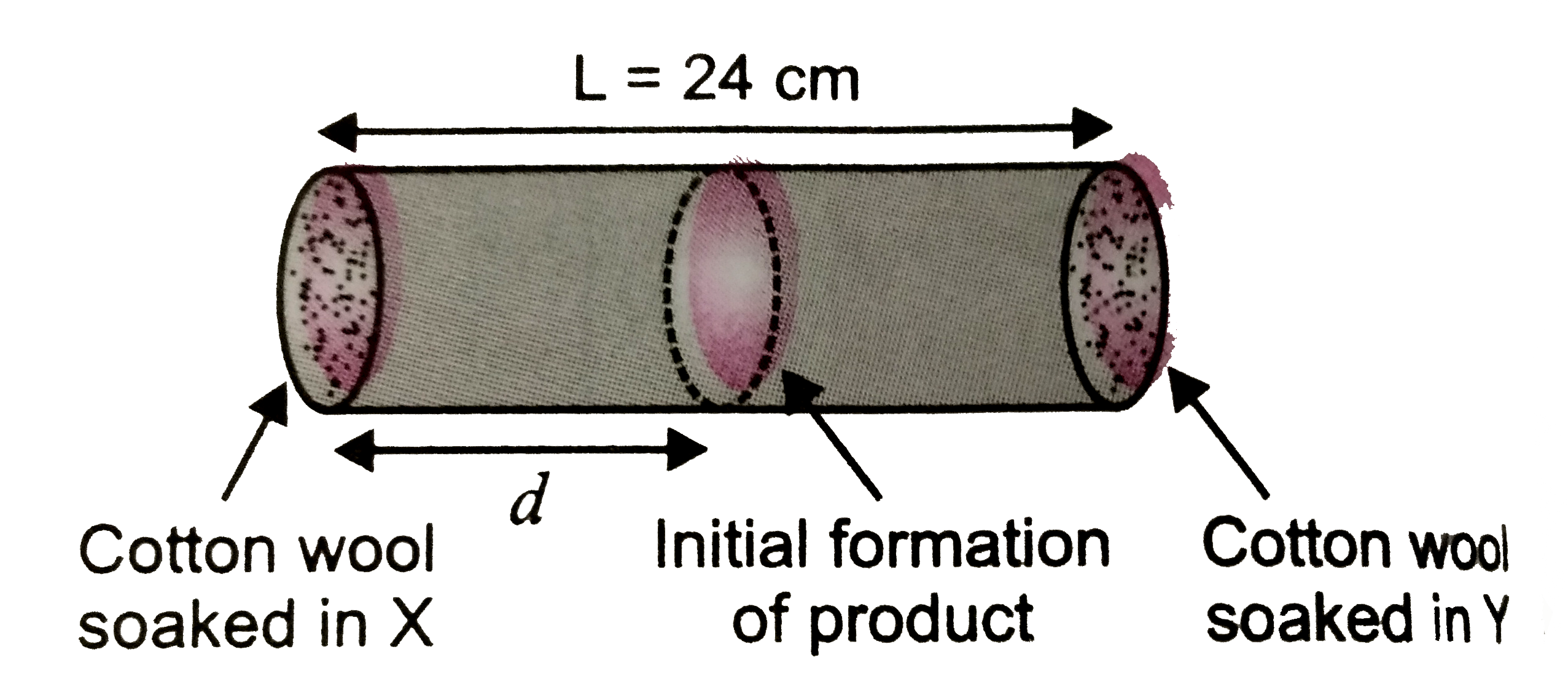
The experimental value of d is found to be smaller than the estimate obtained using Graham's law. This is due to
View Solution
III. Multiple Choice Questions questions and complete solutions for chapter STATES OF MATTER : GASES AND LIQUIDES of PRADEEP CHEMISTRY (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 CHEMISTRY STATES OF MATTER : GASES AND LIQUIDES
- ADDITIONAL QUESTIONS (LONG ANSWER QUESTIONS)
- ADDITIONAL QUESTIONS (SHORT ANSWER QUESTIONS) (Differentiating three states of matter and intermolecular forces)
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS ) Behaviour of real gases and van der Waals equation
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS ) Differentiating three states of matter and intermolecular forces
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS ) Kinetic theory of gases, kinetic energy and molecular speeds
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS ) Liquefaction of gases and critical temperature
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS ) Liquid state and properties of liquids (vapour pressure, surface temsion and viscosity)
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER QUESTIONS ) Measurement of mass, volume, temperature and pressure, gas laws and ideal gas equation
- ADVANCED PROBLEMS (FOR COMPETITIONS)
- ANALYTICAL (QUESTIONA AND PROBLEMS) QUESTIONS
- ANALYTICAL (QUESTIONA AND PROBLEMS) QUESTIONS (PROBLEMS)
- ASSERTION AND REASON TYPE QUESTIONS
- COMPETITION FOCUS (Behaviour of real gases and van der Waals equation)
- COMPETITION FOCUS (Differentiating three states of matter and intermolecular forces)
- COMPETITION FOCUS (Kinetic theory of gases, kinetic energy and molecular speeds
- COMPETITION FOCUS (Liquefaction of gases and critical temperature)
- COMPETITION FOCUS (Liquid state and properties of liquid)
- COMPETITION FOCUS (Measurement of mass, volume, temperature and pressure, gas laws and ideal gas equation
- COMPETITION FOCUS (Miscellaneous)
- CONCEPTUAL QUESTIONS (Behaviour of real gases and van der Waals equation
- CONCEPTUAL QUESTIONS (Differentiating three states of matter and intermolecular forces
- CONCEPTUAL QUESTIONS (Kinetic theory of gases, kinetic energy and molecule speeds
- CONCEPTUAL QUESTIONS (Liquefaction of gases and critical tempetature
- CONCEPTUAL QUESTIONS (Liquid state and properties of liquids ) (vapour pressure, surface tension and viscosity)
- CONCEPTUAL QUESTIONS (Measurement of mass, volume, temperature and pressure, gas laws and ideal gas equation
- CURIOSITY QUESTION
- FILL IN THE BLANK
- II. Multiple Choice Questions
- III. Multiple Choice Questions
- IV MATCHING TYPE QUESTIONS
- LONG ANSWER QUESTIONS
- MULTIPLE CHOICE QUESTIONS-II
- NCERT EXEMPLAR PROBLEMS (MULTIPLE CHOICE QUESTIONS-I)
- PROBLEM
- PROBLEMS FOR PRACTICE
- QUESTIONS AND EXERCISES WITH ANSWERS
- SAMPLE PROBLEM
- SHORT ANSWER QUESTIONS
- TEST YOUR GRIP
- V MATRIX-MATCH TYPE QUESTIONS
- VI INTEGER TRPE QUESTIONS
- VII. NUMERICAL VALUE TYPE QUESTIONS
- VIII. ASSERTION-REASON TYPE QUESTIONS (TYPE-I)
- VIII. ASSERTION-REASON TYPE QUESTIONS (TYPE-II)