Complete Solutions to PROBLEMS FOR PRACTICE of chapter STATES OF MATTER: SOLID MATTER of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | STATES OF MATTER: SOLID MATTER |
| PRADEEP | PROBLEMS FOR PRACTICE |
| Number Of Questions | 63 |
| Academic Year | 2023-24 |
A compound formed by element `X` and `Y` crystallizes in the cubic structure when `Y` atoms are at the corners of the cube and `X` atoms are at the alternate faces. What is the formula of the compound?
View SolutionCalculate the number of atoms in a cubic based unit cell having one atome on each corner and two atoms on each body diagonal.
View SolutionA compound made up of elements `A` and `B` crystallizes in the cubic structures. Atoms `A` are present on the corners as well as face centres whereas atoms `B` are present on the edge centres centres as well as body centre. What is the formula of the compound? Draw the structure of its unit cell.
View SolutionIf three elements P, Q and R crystallise in a cubic unit cell with P atoms at the corners, Q atoms at the cubic centre and R atoms at the centre of each face of the cube, then write the formula of the compound.
View SolutionSodium crystallises in b.c.c unit cell. Calculate the approximate number of unit cells in 9.2 g of solium (Atomic mass of Na = 23u).
View SolutionCalculate the approximate number of unit cells present in 1 g of gold. Given that gold cyrstallises in a face centred cubic lathce (Given atomic mass of gold = 197 u).
View SolutionA solid `AB` has `NaCl` structure. If the radius of the cation `A` is `100` pm, what is the radius of anion `B`?
View SolutionA solid AB has NaCl structure. If the radius of cation `A^(+)` is 170 pm, calculate the maximum possible radius of the anion.
View SolutionWhat is the formula of a compound in which the element Y forms ccp lattice and atoms X occupy 1/3rd of tetrahedral voids ?
View SolutionIn corundum, oxide ions are arranged in hexagonal close packing and aluminium ionsa occpy tow-third of the octaheral voids. What is the formula of corrundum ? .
View SolutionIn solid, oxide ions are arranged in ccp. One sixth of the tetrahedral voids are occupied by the cations (A) while one third of the octahedral voids, are occupied by the cations (B). What is the formula of the compound ?
View SolutionA solid is made up of two elements P and Q , Atoms Q are in ccp arrangement while atoms P occupy all the tetrahdral sites. What is the formual of the compound ?
View SolutionIn chromium (III) chloride `CeCl_(3)` chloride ions have cubic close packed arrangement and Cr (III) ions present in the octahedral voids. What fraction of the octahedral void is occupied ? What fraction of the total number of voids is occupied?
View Solutionwhat is the formula of a compound in which element P forms ccp lattice and atoms of Q occupy 2/3rd of tetrahedral voids ?
View SolutionIf the radii of `Mg^(2+), Cs^(o+), O^(2-), S^(2-)`, and `CI^(Θ)` ions are `0.65, 1.69, 1.40, 1.84`, and `1.81 Å`, respectively, calculate the coordination number of the cation in the crystals of `MgS, MgO`, and `C_(s)CI`.
View SolutionPredict the structure of MgO crystal and the co-ordination number of the cation in which the radii of the cation and anion are 65 pm and 140 pm respectively.
View SolutionPredict the close packed structure of an ionic compound `A^+ B^-` in which the radius of the cation = 148 pm and radius of anion=195 pm. What is the coordination number of the cation ?
View SolutionIf the close-packed cations in an `AB`-type solid gave a radius of `75` pm. What would be the maximum and minimum sizes of the anions filling the voids?
View SolutionA solid `A^(o+)B^(ɵ)` has `NaCl`-type close-packed structure. If the anion has a radius of `250` pm, what should be the ideal radius for the cation? Can a cation `C^(o+)` having radius of `180` pm be slipped into the tetrahedral site of the crystal `A^(o+)B^(ɵ)`? Give reason for your answer.
View SolutionIf the radius of an atom of an elements is `75` pm and the lattice type is body-centred cubic, what is the edge length of the unit cell?
View SolutionThe radius of an atom of an element is `500` pm. If it crystallizes as a face-centred cubic lattice, what is the length of the side of the unit cell?
View SolutionA solid `AB` has `CsCl`-type structure. The edge length of the unit cell is `404` pm. Calculate the distance of closest approach between `A^(o+)` and `B^(Θ)` ions.
View Solutionwhat is the radius of sodium atom if it crystaliizes in bcc structure with the cell edge of 400 pm?
View SolutionGold crystallizes in a face centered cubic lattice. If the length of the edge of the unit cell is 407 pm, calculate the density of gold as well as its atomic radius assuming it to be spherical. Atomic mass of gold = 197 amu.
View SolutionSilver metal crystallises with a face centred cubic lattice. The length of the unit cell is found to be `3.0xx10^(-8)`cm. Calculate atomic radius and density of silver.
Molar mass of Ag`=108 g mol^(-1), N_(A)=6.02xx10^(23)mol^(-1)`).
View SolutionNiobium crystallises in body-centred cubic structure. If the atomic radius is 143.1 pm, calculate the density of Niobium. (Atomic mass = 93u).
View SolutionThe effective radius of an iron atom is `1.42 Å`. It has a rock-salt structure. Calculate its density (Fe = 56)
View SolutionThe edge length of NaCl unit cell is 564 pm. What is the density of NaCl in g/`cm^(3)`?
View SolutionThe compound CuCl has ZnS structure and the edge length of the unit cell is 500 pm. Calculate its density (Atomic mass of Cu = 63, Cl = 35.5)
View SolutionKF and NaCl struture. If the distance between ` K ^(+) and F^(-)` is 269 pm, find the denisty of KF ( ` N_(A) = 6.02 xx 10^(23) "mol"^(-1)` a atomic mass of copper = 63.5
View SolutionCopper crystal has a face-centred cubic lattice structure. Atomic radius of copper atom is 128 pm. Calculate the density of copper. Atomic mass of copper=63.5
View SolutionCopper crystallises into a fee lattice. Its edge length is `3.62 xx 10^(-8)` cm. Calculate the density of copper (atomic mass of Cu=63-5 u, `N_A= 6-022 xx 10^(23) mol^(-1)`).
View SolutionCalculate the density of silver which crystallises in face-centred cubic from. The distance between nearest metal atoms is 287 pm (Molar mass of Ag = `107.87gmol^(-1),(N_(0)=6.022xx10^(23)mol^(-1))`.
View SolutionThe compound CuCl has Zns structure. Its density is 3.4 g `cm^(-3)`. What is the length of the edge of the unit cell ?
View SolutionThe density of a face centred cubic element (atomic mass = 60.2 amu) is 6.25 gm `cm^(-3)`, calculate the edge length of the unit cell.
View SolutionThe density of lead is `11.35 g cm^(-3)` and the metal crystallizes with fee unit cell. Estimate the radius of lead atom. (At. Mass of lead `= 207 g mol^(-1) and NA = 6.02xx10^23 mol^(-1))`
View SolutionWhat is the distance between `Na^(+)` and `Cl^(-)` ions in NaCl crystal if density is `2.165"g cm"^(-3)` ? NaCl crystallises in fcc lattice.
View SolutionLead (II) sulphide crystal has NaCl structure. What is the distance betweeen `Pd^(2+) and S^(2-)` in PhS if its density is ` 12.7 " g cm^(-3)` ? (At .mass of Pb = 207)
View SolutionKBr has fcc struture. The density of KBr is 2.75 g ` cm^(-3)` . Find the distance between ` K^(+) and Br^(-)` , (At mass of Br = 80.0)
View SolutionCalculate the value of Avogadro's number from the following data : Density of KF = ` 2.48 " g cm"^(-3)` . Distance between ` K^(+) and F^(-) ` KF = 269 pm. (Atomic masses : K = 39 and F = 19 amu)
View SolutionCalculate the Avogadro's number from the following data of AB when AB has NaCl type stucture.
Density of AB = ` 2.48 " g cm"^(-3) , M = 58`
Distnace between ` A ^(+) aned B^(-) ` AB = 269 pm.
View SolutionIron has body centred cubic cell with a cell edge of 286.5 pm. The density of iron is 7.87 g `cm^(-3)`. Use this information to calculate Avogadro's number. (Atomic mass of Fe = 56 `mol^(-3)`)
View SolutionThe well know mineral flourite is chemically calcium fluoride. It is a well known fact that in one unit cell of this mineral, there are four `Ca^(2+)` ions and eight `F^(-)` ions and `Ca^(2+)` ions are arranged in f.c.c. lattice. The `F^(-)` ions fill all the tetrahedral holes in the face centred cubic lattice of `Ca^(2+)` ions. The edge length of the unit cell is `5.46xx10^(-8)` cm. The density of the solid is `3.18"g cm"^(-3)`. Use this information to calculate Avogadro's number (Molar mass of `CaF_(2)=78.0"g mol"^(-1)`)
View SolutionAs element cystallises in BCC structure. The edge length of its unit cell is 288 pm. It the density of the crystals is ` 7.2 g cm^(-3)` , what is the atomic mass of the element ?
(b) How many atoms of the element are presnet in 100g ?
View SolutionAn element with density `11.2 g cm^(-3)` forms a f. c. c. lattice with edge length of `4xx10^(-8)` cm. Calculate the atomic mass of the element. (Given : `N_(A)= 6.022xx10^(23) mol^(-1)`
View SolutionAn element (density =`6.8gcm^(-3)` ) occurs in bcc structure with cell edge of `290"pm"` .Calculate the number of atoms present in `200g` of the element:-
View SolutionTungsten has a density of 19.35 g `cm^(-3)` and the length of the side of the unit cell is 316 pm. The unit cell is a body centred unit cell. How many atoms does 50 grams of the element contain?
View SolutionSodium crystallises in a cubic lattice and the edge length of the unit cell is 430 pm. Calculate the number of atoms in the unit cell. (Atomic mass Na = 23 amu, Density of Na = 0.9623 g `cm^(-3)`)
View SolutionAn element with molor mass `27 g mol^(-1)` forms a cubic unit cell with edge length `4.05 xx 10^(-8) cm`. If its density is `2.7 g cm^(-3)`, what is the nature of the unit cell?
View SolutionUse the data given below to find the type of cubic lattice to which the crystal of iron belongs
a/pm=286 , `rho//g cm^(-3)`=7.86
View SolutionThallium chloride (TICI) crystallizes in a cubic lattice whose edge length is found to be 385 pm. If the density of the solid is found to be ` 7.0 " g cm"^(-3)` , predict the type of lattice to which the crystals of TICI belong .
(Atomic mass of TI = 204, Cl = 35.5)
View SolutionIron (II) oxide has a cubic structure and each unit cell has side 5 Å . If the density of the oxide is 4 g ` cm^(-3)` Calculate the number of ` Fe^(2+) and O^(2+)` ions presnent in each unit cell ( Molar mass of FeO = 72 ` " g mol"^(-1)`
`N_(A) = 6.02 xx 10^(23) "mol"^(-1)` )
View SolutionAn element has atomic mass `93 g mol^(-1)` and density `11.5 g cm^(-3)`. If the edge length of its unit cell is 300 pm, identify the type of unit cell.
View SolutionAn element crystallizes in a f.c.c. lattice with cell edge of 250 pm. Calculate the density if 300 g of this element contain `2 xx 10^(24)` atoms.
View SolutionA crystal of lead (II) sulphide has NaCl strcuture . In this crystal the shorest distance between a `Pb^(2+)` ion and `S^(2-)` ion is 297 pm . What is the volume the of unit cell in lead sulphide ?
View SolutionThe unit cube length for `LiCl` (`NaCl` structure) is `5.14 Å`. Assuming anion-anion contact, calculate the ionic radius for chloride ion.
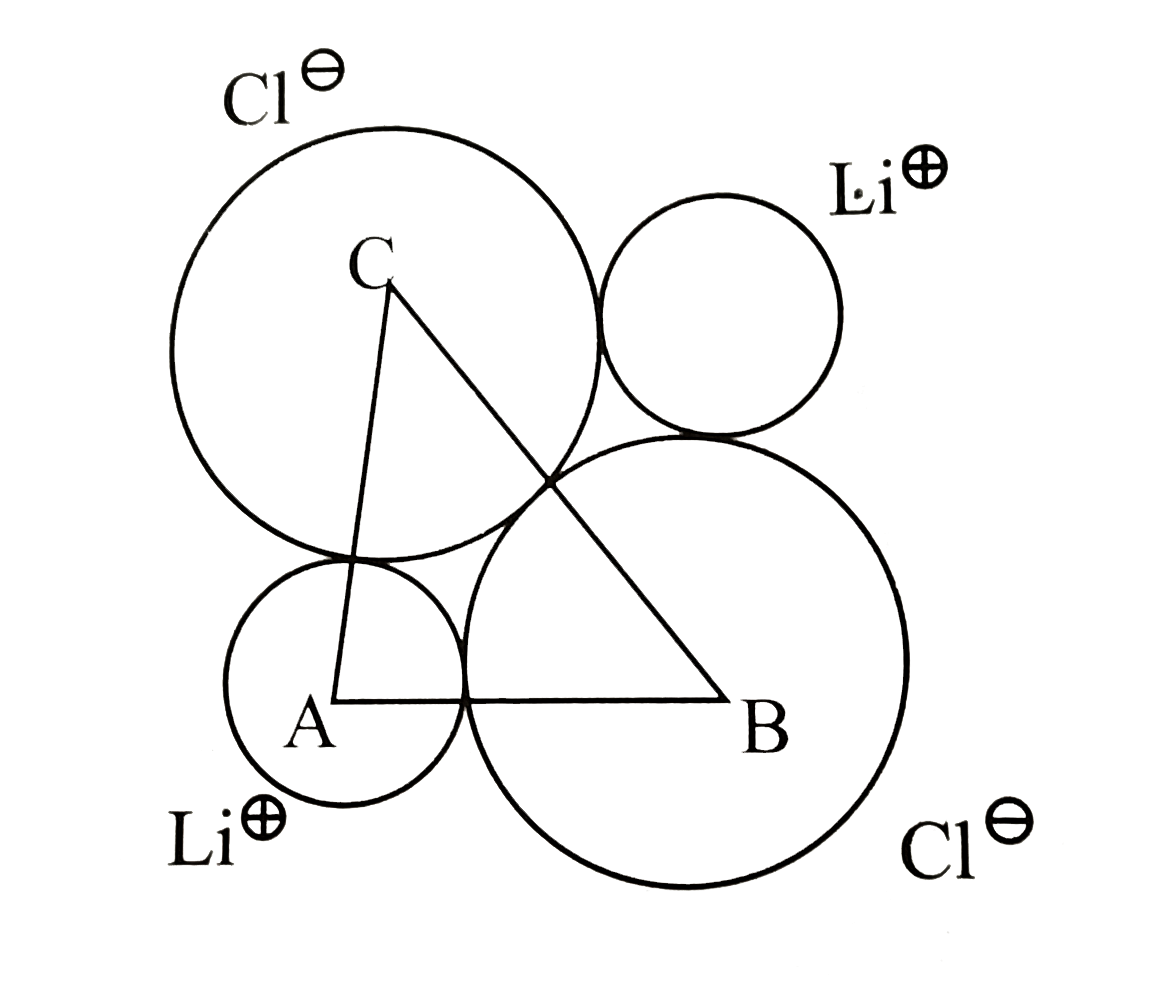
View SolutionA compound AB crystallises in bcc lattice with the unit cell edge length of 380 pm. Calculate (i) the distance between oppositely charged ions in the lattice ,(ii) radius of `B^-` if the radius of `A^+` is 190 pm
View SolutionAn element A crystallises in fcc structure. 200 g of this element has `4.12xx10^(24)` atoms. If the density of A is `7.2"g cm"^(-3)`, calculate the edge length of the unit cell.
View SolutionA metal (atomic mass = 50 ) has a body centred cubic crystal structure. If the density of the metal is 5.96 g `cm^(-3)`, calculate the volume of the unit cell.
View SolutionAluminium metal forms a cubic face centred closed packed crystal structure. Its atomic radius is `125xx10^(-12)`m.
(a) Calculate the length of the side of the unit cell.
(b) How many unit cells are there in `1.0m^(3)` of aluminium?
View SolutionA uni-univalent ionic crystal AX is composed of the following radii (arbitrary units) :
`{:(A^+,A^-),(1.0,2.0):}`
Assuming that ions are hard spheres , predict giving reasons whether the crystal will have sodium chloride cesium chloride structure. Calculate the volume of the unit cell.
View SolutionAn element 'X' (At mass = `40 "g mol"^(-1)`) having fcc structure, has unit cell length of 400 pm. Calculate the density of 'X' and the number of unit cells in 4 g in 'X' `(N_A=6.022xx10^23 "mol"^(-1))`
View SolutionAnalysis shows that a metal oxide has the empirical formula `M_(0.96)O_(1.00)`. Calculate the percentage of `M^(2+)` and `M^(3+)` ions in the sample.
View Solution
PROBLEMS FOR PRACTICE questions and complete solutions for chapter STATES OF MATTER: SOLID MATTER of PRADEEP CHEMISTRY (HINGLISH) of Class 11
All Exercises from PRADEEP Class 11 CHEMISTRY STATES OF MATTER: SOLID MATTER
- ADDITIONAL QUESTIONS ( LONG ANSWER )
- ADDITIONAL QUESTIONS ( SHORT ANSWER )
- ADDITIONAL QUESTIONS (VERY SHORT ANSWER )
- ADVANCED PROBLEMS
- ANALYTICAL (PROBLEMS )
- ANALYTICAL (QUESTION)
- COMPETITION FOCUS (ASSERTION-REASON)
- COMPETITION FOCUS (I.MULTIPLE CHOICE)
- COMPETITION FOCUS (II.MULTIPLE CHOICE)
- COMPETITION FOCUS (III.MULTIPLE CHOICE)
- COMPETITION FOCUS (INTEGER)
- COMPETITION FOCUS (MATCHING)
- COMPETITION FOCUS (NUMERICAL)
- CONCEPTUAL
- CURIOSITY
- NCERT
- NCERT (EXERCISE)
- NCERT EXEMPLAR PROBLEMS (ASSERTION AND REASON)
- NCERT EXEMPLAR PROBLEMS (LONG ANSWER)
- NCERT EXEMPLAR PROBLEMS (MATCHING)
- NCERT EXEMPLAR PROBLEMS (MULTIPLE CHOICE- I)
- NCERT EXEMPLAR PROBLEMS (MULTIPLE CHOICE- II)
- NCERT EXEMPLAR PROBLEMS (SHORT ANSWER)
- PROBLEM
- PROBLEMS FOR PRACTICE
- TEST YOUR GRIP (FILL IN BLANKS)
- TEST YOUR GRIP (MULTIPLE CHOICE)