Complete Solutions to Example of chapter SOME BASIC CONCEPTS OF CHEMISTRY of Class 11 book with complete answers and questions
| Class 11 | CHEMISTRY |
| Chapter | SOME BASIC CONCEPTS OF CHEMISTRY |
| R SHARMA | Example |
| Number Of Questions | 51 |
| Academic Year | 2023-24 |
Calculate the density of silver if a silver coin has a mass of `16.6 g` and occupies a volume of `1.58 cm^(2)`
Strategy: Divide the mass of object by its volume.
View SolutionIn a certain car battery, the density of s8lphuric acid is `1.41 g ML^(-1)`. Caluculate of mass of `242 mL` of the acid.
Strategy: Reaarange the densiy equation (1.1).
View SolutionConvert the meltign point f lead `(327.5^(@)C)` to degress Fabhermit and the boling point of ethmod `(172.9^(@) F)` to degress Celsius.
Strategy: Use Eqs(1.3) or (1.4) to carry out the desired conversion.
View SolutionFind the Faharenhit temperature when the abosuoulte temperature is `400 K`
Strategy: First convert Kelvin to degress Celsius using to Eq. (1.2). Then carry ou t the next converstion from degree Celsius to Fahrenheit.
View SolutionDetermine the number fo significant figures in the following measured quanttities:
(i) `478 cm`, (ii) `7.01 g`
(iiI) `0.852 m`, (iv) `0.034 kg`
(v) `1.410xx10^(22)` atoms, (vi) `8000 mL`.
Strategy: Use the simple rules mentioned above to count the number of significant figures.
View Solution(i) Add `73.24 mL` and `20.3 mL` (ii) Subtract `21.2342 g` foru `27.87 g`
Strategy: We first ensure that the quatities to be added or subtracted are expressed in the same units. We carry out the adition or subtraction. Then we follow rule 1 to express the answer to the correct number of significant figures, i.e., in the final answer, the number of right of the decimal point should be equal to the number of digits after the decimal point.
View SolutionWhat is the area of a recantangel `12.34 cm` wide and `1.23 cm` long?
Stargetey: The area of a rectangler is its length times its width. First, we must check that the width and length are expressed in the same units. Then we mutiply the length by the width. Finally, we follow rule 3 to find the correct number fo significant figures. The Units for the result are equal to the product of the units for the individual terms in the multiplication.
View SolutionIf an object has mass `0.2876 g`, then find the mass of nine such objects.
Strategy: Follow rule 3, but keep in mind that extact numbers obtained from determinos (e.g. dozen) or by counting the number of objects have an infinite number of significant figures.
View SolutionLength conserversion: Convert `58.7 m` to centimeters
Strategy: Express the problem as
`? Cm = 58.7 m`
Use definiton `1 cm = 1xx10^(-2) m`.
Now choose the unit factor has the meters in the denominator,
`(1 cm)/(1xx10^(-2) m) = 1`
View SolutionLength conserversion: Angstrom `(Å)`, a unit of length `(1xx10^(-10)m)` is commonly used to describe the radii of atoms, which are often expressed in other unirs. Find the radius of a sillicon atoms `(1.17 Å)` in centimeters and nanometers. ltbgt Strategy:
`Å rarr m rarr cm`
`Å rarr m rarr nm`
Use th e equations `1 Å = 1xx10^(-10) m, 1 cm = 1xx10^(-2) m`, and `1mm = 1xx10^(-9) m` to construct the unit factors that convert `1.17 Å` to the required units.
View SolutionMass conversion: A sample fo platinum has a mass of `0.432 mg`. What is its mass in kilogram?
Strategy: Consturct the required unit factors using the relationship `1g = 1000 mg` and `1 kg = 1000 g` and follow the sequence
`mg rarr g rarr kg`
View SolutionVolume conversion : The volume of a cubical is `7.6 m^(3)`. What is the volume in cubci centimeter ?
Strategy : First find the suitable unit factor using the relanship `1 cm = 10^(-2) m`. The cube this unit factor.
View SolutionDenstity conversion : The density of liquid metal, mercucy,n is `13.6 g cm^(-3)`. What is the density in `kg m^(-3)` ?
Strategy : We need two unit factors-one to convert gram to kilogram and the other to convert cubic meter to cubic centimeter. Use the relationships `1 kg = 1000g` and `1 cm = 1xx10^(-2) m`.
View SolutionLaw of conservation of mass: When `4.2 g` of sodioum hydrogen carbone `(NaHCO_(3))` is added to a solution of acertc aacid `(CH_(3) COOH)` weighting `10.0 g` then `2.2 g` of carbon diosxed `(CO_(2))` is released into the atmosphere and the residue ledft weighs `12.0 g`. Show that these observation are in agreement with the law of conservation of mass.
Strategy: Find the sum total of mass of recants before the reaction and sum total of mass of products after the reaction.
View Solution`1.59 g` of first sample fo cupric oxide `(CuO)` on comple reduction by hydrogen `(H_(2))` gas gave `1.27 g` of pure copper `(Cu)` metal. Secound pure sample of curpic oxide weighing `3.18 g` yieled `2.54 g` of pure copper metal on complete refuction by hydrogen gas. Show that the law of definite proportions is valid.
Strategy: Find the ratio by mass of copper to oxygen in both the samples.
View SolutionLaw of multipole proportions: sulphur forms two chlowides. `A 30.00 h` sample of one electric decomposes to give `5.53 g` fo sulphur `(S)` and `24.47 g` fo chloring `(CI) A 30.00 g` sample of the other chloride decomposes to give `3.93 g` of `S` and `26.07 g` of `CI`. Show that these compounds obey the law of multiple prooportions.
Strategy: First we calculate the mass of `Cl` that combines with `1 g` of `S` in each compound. Then we determine the ratio of the different masses fo `Cl` for the two compounds.
View SolutionCopper sulphide `(Cus)` contains `66.5 % Cu` copper axide `(CuO)` contains `79.9% Cu` and sulphur trioxide `(SO_(3))` containts `40% S`. Shows that these compounds obey the law of recipreocal proportions.
Strategy: Elements `S` and `O` chemically combine seperately with element `Cu` to from `Cus` adn `CuO`. Elements `S` and `O` also chemicaly combine with each other to form `SO_(3)`. Find the ratio of masses of `S` to `O` combining with a given mass of `Cu` and also find the ratio of masses of `S` to `O` in`SO_(3)`.
View SolutionLaw pf combining volumes: if ten volumes of dihydrogen gas react with five valumes of diaxygen gas, how many volumes of water vapor are produced ?
Strategy : According to the law of combining volumes, if the product is a gas (or vapor), its volume is related to the volume of the gaseous reactants by a simple ratio.
View SolutionAvogadro's law: When half a liter of carbon dioxide gas is passed over red coke, a reducing agent, the volume becomes `700 mL`. Assuming that volumes are measured at the same temperature and pressure, find the composition of product.
Strategy: The term composition indicates that we are dealing with a mixture. Write the correct balanced equation and use volume in place in moles.
View SolutionCalculation of average atomic mass: The atomic attoms fo the two stbale isopes of boron, `._(5)^(10)B (19.78%)` and `._(11)^(5)B (80.22%)`, are `10.0129 u` and `11.0093 u`, respectively, Calculate the average atomic mass of boron.
Strategy : The atomic mass of an element existing in nature as istopes is the weighted average of the istope masses, Thus, multiply the fracton of each isotope by its mass and add these numbers to obtain the mass of born.
View SolutionCalculation of istopic abundance: The atomic mass of gallium `(Ga)` is 69.72 u. The masses of the naturally occuring istopes are `68.9257 u` for `._(69)^(31)Ga` and `70.9249 u` for `._(71)^(31) Ga`. Calculate the present adundance of each istope.
Strategy : We present the fraction of each istope algebraically. The atomic mass of an element is the weighted average of the istope masses, which equals the sum of the masses of each isotope times the fraction of that isotope.
View SolutionEmprical formula: Write the emprical formulas for the follwing molecule compounds: (i) dinitrogen tetoxide `(N_(2) O_(4))`, (ii) acterylene `(C_(2) H_(12) O_(6))`.
Strategy: Divide all the subscipts, if possible by a sutiable number so that the subscips are convered to the smllest whole numbers.
View SolutionMolecule mass: Calculate the molecule mass of vitamin `C` or ascrobic acid `(C_(6) H_(8) O_(6))` using rounded values for atomic masses.
Strategy: Add the atomic masses of the elements in the formula, each multipled by the number of times the element occurs.
View SolutionPlatinum `(Pt)` is a hard silvery-white metal. How many moles of `Pt` atoms are in `292.64 g` of `Pt` metal?
Strategy: Elementary entiteis of `Pt` metal are atoms. The atomic mass of `Pt` is `195.09 u` thus, the molar mass of `Pt` is `195.09 "g mol"^(-1)`.
View SolutionHydrogen cyanice `(HCN)` is a volatile, colorless liquid with the odor of certain fruit pits (such as peach and cherry pits). The compound is highly posisonous. How many molecules are there in `56 mg HCN` the average foxic dose ?
Strategy : The molecule mass of `HCN` is 27.03 amu. Thus, its molar mass is 27.03 g. First convert the mass of sample in moles, then convert moles to number of molecules.
grams of `HCN rarr` mole of `HCN rarr` molecules of HCN
View SolutionGold `(Au)` is a precious metal used mainly in jewelry. What is the mass in grams of one `AU` atoms ?
Strategy : We expect that the mass of a single `Au` atoms in grams would be very small number. The atomic mass of `Au` is `197.97 u`. Thus, its molar mass is `196.97g. Because each mode of a substance contains Avogadro's number of units of that substance contains. Avogadro's number of units of that substance dividing the mass of the substance in one mole (molar mas) by Avogadro's constant gives the mass of that unit of substnace.
View SolutionMass of molecules : What is the mass (in grams of 10.0 billion sulphur dioxide `(SO_(2))` molecules?
Strategy : The molecular mass of `SO_(2)` is 64.1 u. Thus, its mole and then find the mass using Eqs(1.7).
View SolutionNumber of molecules: What is the number of molecules `11.2 L` of nitrogen dioxide gas `(NO_(2))` at `NTP`
Strategy: First find the number of molecules using Avagadro's constant.
View SolutionNumber of molecules: What is the number of molecules in a diatomic gas present in `1 L` flask at `0^(@) C` and under a pressure of `7.6xx10^(-19) mm Hg`?
Strategy : Express the pressure in atmosphers and use Eq.(1.10) to calculate the number of moles. Using Avoagdro's constant,find the number of molecules.
View SolutionNumber of atoms: How many `C` atoms are present in `342.3g` of table sugar or surose `(C_(12) H_(22) O_(11)` ?
Strategy : The molecule mass of surcrose is `342.3 u`. Thus, its molar mass is 342.3 g. First calculate the number of moles, then calculate the number of molecules, and finally use the information that there are `12 C` atoms in every molecule to find the number of `C` atoms.
grams `rarr` moles of sucrose `rarr` molecules of surcrose
`rarr` number of `C` atoms
View SolutionMole conept: Calculate the follwing in `48g` of oxygen gas (diaxygen) at room temperature `(25^(@) C)`: (i) moles of `O_(2)`, (Ii) number of `O_(2)` molecules, (iii) number of `O` atoms, and (iv) number of electrons.
Strategy: The molecular mass of dioxygen `(O_(2))` is `32 mu`Thus, its molar mass is `32.0g mol^(-1)`, Now, use the needed information:
(a) one mole of `O_(2)` contains Avogadro's number of `O_(2)` molecules,
(b) one `O_(2)` molecules contains 2 oxygen atons, and `(c)` one oxygen atom contains 8 electrons.
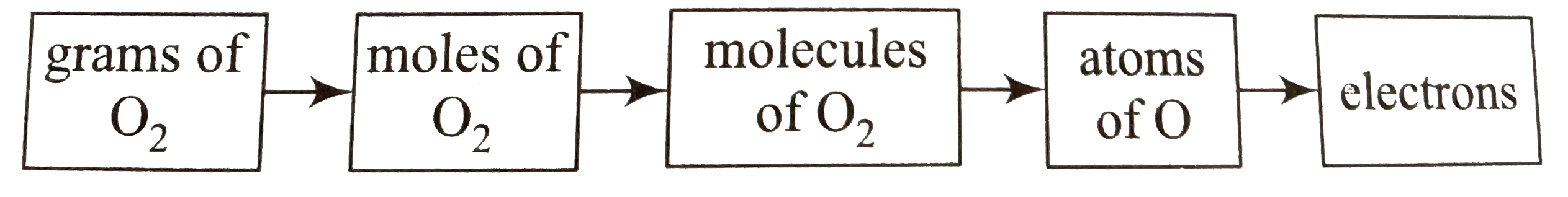
View SolutionPercentage composition: Ammonia `(NH_(3))` si a pungent smelling very soluble gas, given an alkatline solution containing ammonnium hydoximate. It is used as a refigerment and for the manufacture fo fertilizers. Calculate the mass percentage fo the elements in ammnia.
Strategy: We need the mass of an element in a given mass of compound. To get this information, we interpect the formula in molar terms and then convert moles to masses. Every molecule of ammonia always has the formula `NH_(3),i.e., 1` mol of `NH_(3)` always contains 1 mol of `N` atoms and 3 mol of `H` atoms.
View SolutionSimplest or empirical formula: Ascorbie acid (vitamin `C`) a white crystalline solid, that is present in fruits and vegetables, curves scury and may help prevent the common cold. It is composed of `40.92%C, 4.58% H`, and `54.50% O` by mass. Determine its emprical formula.
Strategy: Because one mole of atoms of any given element is `6.022xx10^(23)` atoms, the ratio of the numbers of atoms the ratio of the numbers of atoms in any sample fo a compound is the same as the ratio fo motes of atoms is that compound. Thus, the energy is to, find the relative number of moles of each element in the compound and then use the numbers to establish the mole ratio of the elements which in turn give the subsrips in the empral formula. This calculation si carried out as follow:
Step 1: Becuase the sum of all the percentages is `100%` it is conventient to solve this type of problem by considerinf exactly `100g` of the substance, which means `100.00g` of ascoric acid contains `40.92g` of `C, 4.58g` of `H`, and `54.50g` of `O`
Next we need to calculate the number of moles of atoms of each element in the compound.
Step 2: We then obtain teh simplest whole number ratio between these number that gives that ratio of atoms in the sample and hence, the simplest or empirical formula for the compound.
View SolutionBalancing chemical equation: Propance `(C_(3) H_(8))` is a colorless, odorless gas often used as a heating and cooking fuel in rural homes, Write a balanced equation for the combusion reaction of propane with oxygen to yield carbon dioxide and water.
View SolutionMolecular intyerpreation: How many `O_(2)` molecules react with `74 CH_(4)` molecules according to the preccdign equation?
Strategy: The balanced equation tells us that one `CH_(4)` molecule always reacts with two `O_(2)` molecules. Either we go for unitary method or construct a unit factor from the above fact:
`(2 O_(2) "molecules")/(1 CH_(4) "molecule")`
View SolutionNumber of moles formed: How many moles of water are produced when `4.5m` mol of methance reacts with excess oxygen?
Strategy: According to the balanced equation for the combusion of methane,
`CH_(4) + 2O_(2) rarr CO_(2) + 2H_(O)`
1 mol of methance alwyas reacts with 2 mol of oxygen to produce 2 mol of water. Either we use unitary approach or factor- we use unitary approah or factor-label method by constructing the unit factor.
`(2 mol H_(2) IO)/(1 mol CH_(4))`
View SolutionWhat mass of oxygen gas is required to burn completely `2.5 mol` of method?
`underset(underset("reactant")("one"))("Moles of ")rarr underset(underset("reactant")("another"))("Mass of")`
Stragetgy : Use the balanced equation
`{:(CH_(4), + 2O_(2), rarr CO_(2), + 2H_(2) O),(1mol, 2mol,1 mol,2mol),(16.0 g,2(32.0)g,44.0g,2(18.0g)):}`
to find the relationship among moles and grams of reactants :
`underset(CH_(4))("Mole of ")rarr underset(O_(2))("Moles of")rarr underset(O_(2))("grams of")`
View SolutionWhat mass of oxygen gas is required to burn completely `2.5 mol` of methane?
`underset(underset("reactant")("one"))("Moles of ")rarr underset(underset("reactant")("another"))("Mass of")`
Stragetgy : Use the balanced equation
`{:(CH_(4), + 2O_(2), rarr CO_(2), + 2H_(2) O),(1mol, 2mol,1 mol,2mol),(16.0 g,2(32.0)g,44.0g,2(18.0g)):}`
to find the relationship among moles and grams of reactants :
`underset(CH_(4))("Mole of ")rarr underset(O_(2))("Moles of")rarr underset(O_(2))("grams of")`
View SolutionMost combustion reactions occur in excess of `O_(2)` (i.e., more than enough `O_(2)` to burn the substance completely). Calculate the mass of `CO_(2)` (in grams) produced by buring `4.00 mol` of `CH_(4)` in excess `O_(2)`.

Strategy: using the balanced equation
`{:(CH_(4), + 2O_(2), rarr CO_(2), + 2H_(2) O),(1mol, 2mol,1 mol,2mol),(16.0 g,2(32.0)g,44.0g,2(18.0g)):}`
we find out that 1 mol of `CH_(4)` is chemically equivalent to 1 mol of `CO_(2)` or `44.0g` of `CO_(2)`.
View SolutionLimiting reactant: What mass of water `(H_(2) O)` can be formed by the reaction of `3.00g` of `H_(2) (g)` with `29.0g` of `O_(2)(g)`?
Strategy: Using the balanced equation
`{:(2H_(2)(g),+,O_(2)(g),,rarr2H_(2)O(l)),(2mol,,1mol,,2mol),(2(2.00g),,32.0g,,2(18.0g)):}`
find out the numbers fo moles of each reactatn required to react with the other. Using the given masses, calculate the number of moles of each reactant. Finally, identify the limiting recatant and base the rest of the calculate on it.
View SolutionLimiting reactant: Urea `[(NH_(2))_(2) CO]` used as ferlilzer as animal feed, and in polymer industry, is prepared by the reaction between ammonia and carbon dioxide:
`2NH_(3)(g) + CO_(2) (g) rarr (NH_(2))_(2) CO(aq.) + H_(2) O(1)`
In one process , `637.2g` of `NH_(3)` is allowed to react with `11.42g` of `CO_(2)`
(i) Which of the two reactants is the limiting reactant?
(ii) Calculate the mass of `(NH_(2))_(2) CO` formed?
(iii) How much of the excess reagent (in grams) is left at the end of the reaction?
Strategy: (i) Since we cannot tell by inspection which of the two recantants is the limiting reacant, we have to procced by first converting their masses into number of moles. Take each reactnat in turn and ask how many moles of product (urea) would be obtained if each were completely consumed. The reactant that gives the smaller number of moles of producet is the limiting reactant.
(ii) Convert the moles of product obtained to grams of product.
(iii) From the moles of product, calculate to grams fo excess reactant needed int he reaction. Then subtract this qunitity from the grams of the reactant available to find the quanity of the excess reactant remaining.
View SolutionPercent of solute: Calculate the mass of calcium suphate `(CaSO_(4))` contained in `200g` of a `6.00%` solution of `CaSO_(4)`
Strategy: Percent infromation means the solution contains `6.00g` fo `CaSO_(4)` per `100g` of solution. To solve the problem, we can use either unitary method or Eq (1.16) or construct a unit factor.
View SolutionMass of solute : Calculate the mass of `CaSO_(4)` present in `200 mL` of a `6.00%` soultuion of `CaSO_(4)`. The density of the solution is `1.06g mL^(-1)` at `25^(@) C`
Strategy: Find the mass of solution by multiplying the volume of solution wtih its density and then find the mass of `CaSO_(4)` as discussed in the previous example.
View SolutionMole fraction: A solution contains `127g` of merthanot `(CH_(3) OH)` in `108g` of water `(H_(2) O)`. What are the mole fractions of `CH_(3) OH` and `H_(2) O`?
Strategy: Convert the masses of both components to their moles, and them apply the definiton fo mole fraction.
View SolutionMolarity: A solution contains `3.65g` of hydrogen chloride `(HCl)` in `2.00L` of sollution. Calculate the molarity `(M)` of the solution.
Strategy: Convert grams of `HCl` to moles of `HCl` and then apply Eq(1.20).
View SolutionMass of solute: How many grams of barium hydroxide `[Ba(OH)_(2)]` are requirred to prepare `1.75 L` of a `0.0500 M` solution of barium hydroxide?
Strategy: Find the number of moles solute by multiplying the molartiy of solution with its volume and then multiply the number of moles of solute with its molar mass.
View SolutionMolarity: A sample of commercial sulphuric acid is `98% H_(2) SO_(4)` by mass and its specfic gravity is `1.84`. Caculate the molartiy of this sulburic acid solution.
Strategy: The density of a solution (grams per milliliter) is numercially equal to its specific gravity. Thus, the density of the solution is `98% H_(2) SO_(4)` by mass. Thus, every `100g` of soultuon contains `98g` of pure `H_(2) SO_(4)`. From the mass of `H_(2) SO_(4)`. we calculate its moles and from the density , we calculate its volume. Finally, we calculate molartity using its definition.
View SolutionDilution: How many milliliters of `18.4 M H_(2) SO_(4)` are required to prepare `1L` of `0.940 M` solution of `H_(2) SO_(4)`?
Strategy: Since the concentration of the final solution is less than that of the orignal one, this is a dilution process. We are given the molarity of the original solution and the volume `(V_(f))` and molarity `(M_(f))` of the final solution. Thus. Eq (1.21) can be used.
View SolutionMolarlity: An acqueous solution contains `128g` of mehanol `(CH_(2) OH)` in `108g` of water. Calculate the molarity of the solution.
Strategy: Convert the grams of `CH_(3) OH` to moles of `CH_(3) OH` express the mass of `H_(2) O` in kilogram and apply the definition of molality.
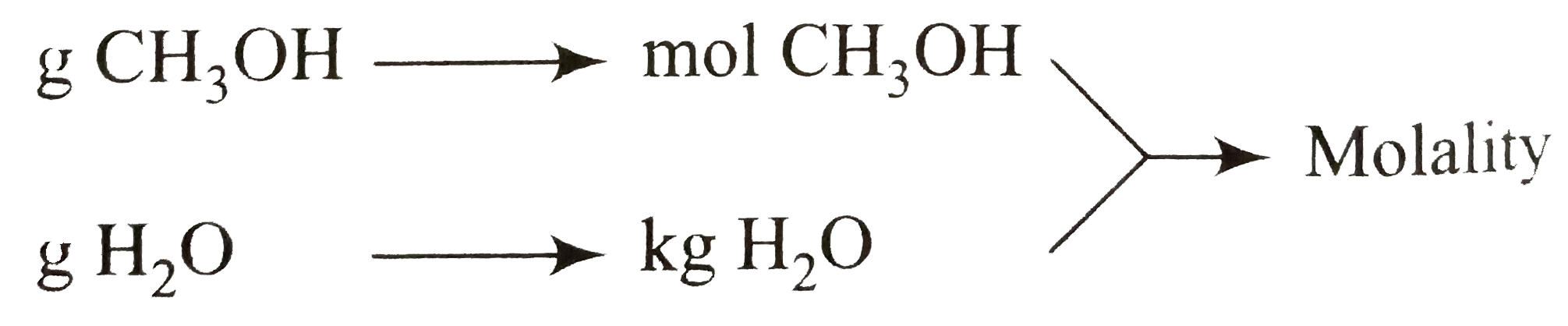
View SolutionNormally: An aquous solution contains `4.202 g` of `HNO_(3)` in `600 mL` of solution. Calculate the normally of solution?
Stragegy: Convert grams of `HNO_(3)` to moles of `HNO_(3)` to moles of `HNO_(3)` and then to equivalents of `HNO_(3)`. Finally , apply the defintion of normally.
`(g HNO_(3))/(L) rarr (mol HNO_(3))/(L) rarr (eq HNO_(3))/(L) rarr (eq HNO_(3))/(L) = N HNO_(3)`
View SolutionNormally and molarity: An aqueous solution contains `9.50g` of barium hydroxide in `200 mL` of solution. Calculate (i) the molartiy and (ii) the normally of the solution.
Strategy : Convert grams of `Ba(OH)_(2)` to moles of `Ba(OH)_(2)` and then calculate molarity. Becuase each formula unit of `Ba(OH)_(2)` furnishes two `Oh` ions, 1 mol `Ba (OH)_(2) = 2 eq Ba(OH)_(2)`. Thus, normally is twice of molarity for `Ba (OH)_(2)` solution.
View Solution
Example questions and complete solutions for chapter SOME BASIC CONCEPTS OF CHEMISTRY of R SHARMA CHEMISTRY (HINGLISH) of Class 11
All Exercises from R SHARMA Class 11 CHEMISTRY SOME BASIC CONCEPTS OF CHEMISTRY
- Archives
- Example
- Follow-up Test 1
- Follow-up Test 10
- Follow-up Test 11
- Follow-up Test 12
- Follow-up Test 13
- Follow-up Test 14
- Follow-up Test 15
- Follow-up Test 16
- Follow-up Test 17
- Follow-up Test 18
- Follow-up Test 19
- Follow-up Test 2
- Follow-up Test 20
- Follow-up Test 21
- Follow-up Test 3
- Follow-up Test 4
- Follow-up Test 5
- Follow-up Test 6
- Follow-up Test 7
- Follow-up Test 8
- Follow-up Test 9
- Question Bank