Complete Solutions to एनसीईआरटी कॉर्नर of chapter प्रायिकता of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | प्रायिकता |
| RAJEEV BANSAL | एनसीईआरटी कॉर्नर |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
प्रतिदर्श समष्टि ज्ञात कीजिए
एक सिक्के को तीन बार उछाला गया है ।
View Solutionप्रतिदर्श समष्टि ज्ञात कीजिए
एक पासा दो बार फेका गया है ।
View Solutionप्रतिदर्श समष्टि ज्ञात कीजिए
एक सिक्का चार बार उछाला गया है ।
View Solutionप्रतिदर्श समष्टि ज्ञात कीजिए
एक सिक्का उछाला गया है और एक पासा फेका गया है ।
View Solutionएक सिक्का उछाला गया है और केवल एक दशा में, जब सिक्के पर चित प्रकट होता है एक पास फेंक जाता है।
View SolutionX कमरे में 2 लड़के और 2 लड़कियाँ तथा Y कमरे में 1 लड़का और 3 लड़कियाँ है । उस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए
View Solutionएक पासा लाल रंग का , एक सफेद रंग का और एक अन्य पासा नील रंग का एक थैले में रखे है । एक पासा यादृच्छया चुना गया और फेका गया है । पासे का रंग और इसके ऊपर के फलक पर प्राप्त संख्या को लिखा गया है । प्रतिदर्श समष्टि का वर्णन कीजिए ।
View Solutionएक परीक्षण में दो बच्चो वाले परिवार में लड़के-लड़कियों की संख्याओं को लिखा जाता है :
यदि हमारी रूचि एक बात को जानने में है कि जन्म के क्रम में बच्चा लड़का है या लड़की तो तब प्रतिदर्श समष्टि क्या होगी ?
View Solutionएक परीक्षण में दो बच्चो वाले परिवार में लड़के-लड़कियों की संख्याओं को लिखा जाता है :
यदि हमारी रूचि किसी परिवार में लड़कियों कि संख्या जानने कि है तब प्रतिदर्श समिष्टि क्या होगी ?
View Solutionएक डिब्बे में एक लाल तथा एक जैसी तीन सफेद गेंदे है । दो गेंदों उत्तरोत्तर बिना प्रतिस्थापित किये यादृच्छया निकली जाती है । इस परीक्षण का प्रतिदर्श समष्टि कीजिए ।
View Solutionएक परीक्षण में एक सिक्के को उछाला जाता है और यदि उस पर चित प्रकट होता है तो उसे पुनः उछाला जाता है । यदि पहली बार उछालने पर पट प्राप्त होता है तो एक पासा फेका जाता है । प्रतिदर्श समष्टि ज्ञात कीजिए ।
View Solutionमान लीजिए बल्बों के एक ढेर में तीन बल्ब यादृच्छया निकले जाते है । प्रत्येक बल्ब को जाँचा जाता है उसे खराब (D ) या ठीक (N ) में वर्गीकृत करते है । इस परिषन का प्रतिदर्शी लिखिए ।
View Solutionएक सिक्का उछाला जाता है यदि परिणाम चित हो तो एक पासा फेका जाता है । यदि पासे पर एक सम संख्या प्रकट होती हो तो पासे को पुनः फेका जाता है । इस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए ।
View Solutionकागज कि चार पर्चियों पर संख्याएँ 1 ,2 3 तथा 4 अलग-अलग लिखी गई है । इन पर्चियों को को एक डिब्बे में रखकर भली-भाँती मिलाया गया है । एक व्यक्ति डिब्बे में से दो पर्चियाँ एक के बाद दूसरी बिना प्रतिस्थापित किये निकलता है । इस परीक्षण का प्रतिदर्श समष्टि ज्ञात कीजिए ।
View Solutionएक परीक्षण में पासा फेका जाता है और यदि पासे पर प्राप्त संख्या सम हो तो एक सिक्का उछाला जाता है । यदि पासे पर प्राप्त संख्या विषम हो तो सिक्के को दो बार उछाला जाता है । प्रतिदर्श समष्टि लिखिए ।
View Solutionएक सिक्का उछाला गया यदि उस पर पट प्रकट होता है तो एक डिब्बे में से जिसमे 2 लाल और 3 काली गेंदे राखी है, एक गेंद निकलते है। यदि सिक्के पर चित प्रकट होता है तो एक पासा फेका जाता है । इस परीक्षण का प्रतिदर्श समष्टि लिखिए ।
View Solutionएक पासे को बार-बार तब तक फेका जाता है जब तक उस पर 6 प्रकट न हो जाये । इस परीक्षण का प्रतिदर्श समष्टि क्या है ?
View Solutionएक पासा फेका जाता है । मान लीजिए घटना E पाए पर संख्या '4 ' दर्शाता है तथा घटना F "पाए पर सैम संख्या प्रकट होती है ।" क्या E तथा F परस्पर अपवर्जी है ?
View Solutionएक पास फेंका जाता है । घटनाओ का वर्णन कीजिए-
A :संख्या 7 से कम है ।
View Solutionएक पास फेंका जाता है । घटनाओ का वर्णन कीजिए-
B :संख्या 7 से बड़ी है ।
View Solutionएक पास फेंका जाता है । घटनाओ का वर्णन कीजिए-
C :संख्या 3 का गुणज है ।
View Solutionएक पास फेंका जाता है । घटनाओ का वर्णन कीजिए-
D :संख्या 4 से कम है ।
View Solutionएक पास फेंका जाता है । घटनाओ का वर्णन कीजिए-
E :4 से बड़ी सैम संख्या है ।
View Solutionतीन सिक्कों को एक बार उछाला जाता है। मान लीजिए की घटना तीन चित दिखाना को A से ,घटना दो चित और एक पट दिखाना को B से. घटना तीन पट दिखाना को C और घटना पहले सिक्के पर चित दिखाना को D से निरूपित किया गया है। बताइये की इनमे से कौन सी घटनाएँ (i) परस्पर अपवर्जी है? (ii) सरल है (iii) मिश्र है?
View Solutionतीन सिक्के एक बार उछाले जाते है, वर्णन कीजिए :
दो घटनाएँ जो परस्पर अपवर्जी है।
View Solutionतीन सिक्के एक बार उछाले जाते है, वर्णन कीजिए :
तीन घटनाएँ जो परस्पर अपवर्जी तथा नि: शेष है।
View Solutionतीन सिक्के एक बार उछाले जाते है, वर्णन कीजिए :
दो घटनाएँ जो परस्पर अपवर्जी नहीं है ।
View Solutionतीन सिक्के एक बार उछाले जाते है, वर्णन कीजिए :
दो घटनाएँ जो परस्पर अपवर्जी है, परन्तु नि : शेष नहीं है।
View Solutionतीन सिक्के एक बार उछाले जाते है, वर्णन कीजिए :
तीन घटनाएँ जो परस्पर अपवर्जी है , किन्तु नि: शेष नहीं है ।
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
A'
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
B-नहीं
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
A या B
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
A और B
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
A किन्तु C नहीं
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
B या C
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
B और C
View Solutionदो पासे फेंके जाते है । घटनाएँ निम्न प्रकार से है :
A: पहले पासे पर सम संख्या प्राप्त होना ।
B: पहले पासे पर विषम संख्या प्राप्त होना ।
C:पासो पर प्राप्त संख्याओं का योग `le 5 ` होना
घटनाओ का वर्णन कीजिए :
B या C
View Solutionएक सिक्का दो बार उछाला जाता है, कम-से-कम एक पट प्राप्त होने की क्या प्रायिकता है ?
View Solutionएक पासा फेंका जाता है । घटनाओ की प्रायिकता ज्ञात कीजिए :
एक अभाज्य संख्या प्राप्त हो ।
View Solutionएक पासा फेंका जाता है । घटनाओ की प्रायिकता ज्ञात कीजिए :
तीन या तीन से बड़ी संख्या उपस्थित हो ।
View Solutionएक पासा फेंका जाता है । घटनाओ की प्रायिकता ज्ञात कीजिए :
1 या 1 से छोटी संख्या उपस्थित हो ।
View Solutionएक पासा फेंका जाता है । घटनाओ की प्रायिकता ज्ञात कीजिए :
6 से बड़ी संख्या उपस्थित हो ।
View Solutionएक पासा फेंका जाता है । घटनाओ की प्रायिकता ज्ञात कीजिए :
6 से छोटी संख्या उपस्थित हो ।
View Solutionप्रतिदर्श समष्टि `S={w_(1),w_(2),w_(3),w_(4),w_(5),w_(6),w_(7)}` के परीक्षणों के लिए निम्नांकित में से कौन-से प्रायिकता निर्धारण वेध नहीं है।
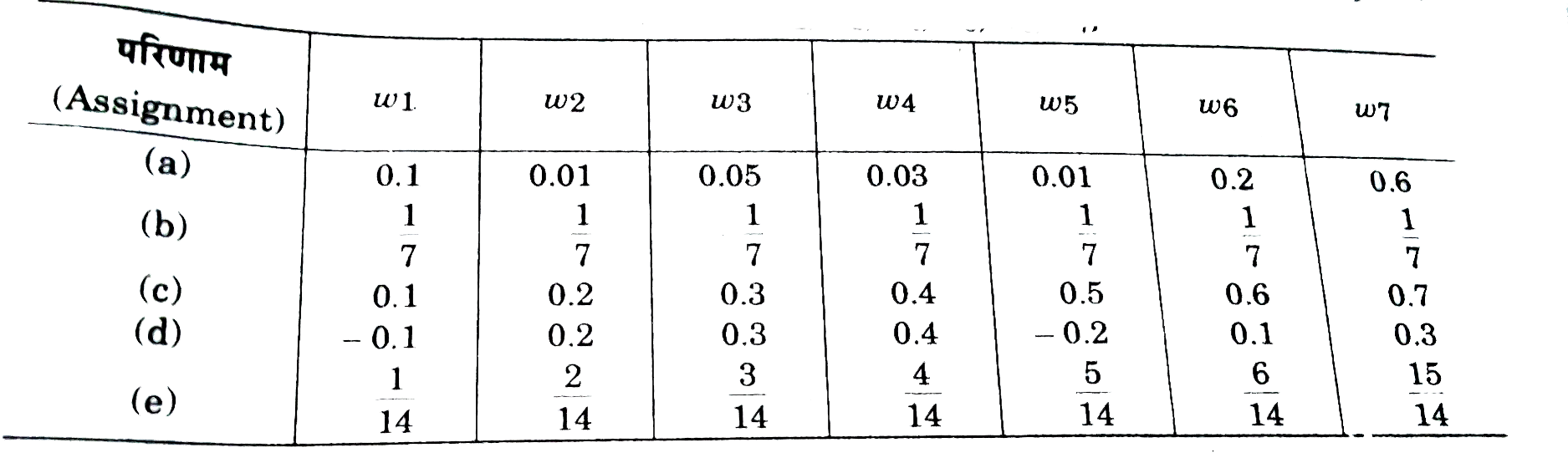
View Solutionताश की एक गड्डी के 52 पत्ते में से एक पत्ता यादृच्छया निकला गया है :
प्रतिदर्श समष्टि में कितने बिंदु है ?
View Solutionताश की एक गड्डी के 52 पत्ते में से एक पत्ता यादृच्छया निकला गया है :
पत्ते का हुकुम का इक्का होने की प्रायिकता क्या है ?
View Solutionताश की एक गड्डी के 52 पत्ते में से एक पत्ता यादृच्छया निकला गया है :
प्रायिकता ज्ञात कजिए (i ) इक्का है (ii ) काळा रंग का है ।
View Solutionएक नाव्य सिक्का जिसके एक तल पर '1 ' और दूसरे तल पर 6 अंकित है तथा एक अनभिनात पासा दोनों को एक साथ उछाला जाता है । प्रायिकता ज्ञात कीजिए कि संख्याओं का योगफल (i ) 3 है, (ii ) 12 है ।
View Solutionनगर परिषद् में 4 पुरुष 6 महिलाएँ है, यदि एक समिति के लिए यादृच्छया एक परिषद् सदस्य चुना गया है , एक स्त्री के चुनने कि सम्भावना क्या है ?
View Solutionएक अनभिनात सिक्के को चार बार उछाला जाता है और एक व्यक्ति प्रत्येक चित पर एक रुपया जीतता है और प्रत्येक पट रु `1.50` हारता है । इस परीक्षण के प्रतिदर्श समष्टि से ज्ञात कीजिए कि आप चार उछालो में कितनी भिन्न राशियाँ प्राप्त कर सकते है । साथ ही इन राशियों में से प्रत्येक प्रायिकता भी ज्ञात कीजिए ।
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
तीन चित (Head ) प्रकट होना,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
दो चित (Head ) प्राप्त हो,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
न्यूनतम 2 चित (Head )प्रकट होना,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
अधिकतम 2 चित प्रकट होना,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
एक भी चित (Head )प्राप्त न होना,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
तीन पट (Tail )प्राप्त हो ,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
तथयत: दो पट प्राप्त हो,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
कोई भी पट प्राप्त न हो,
View Solutionतीन सिक्के एक बार उछाले जाते है । प्रायिकता ज्ञात कीजिए :
अधिकतम 2 पट प्राप्त होना ।
View Solutionकिसी घटना A की प्रायिकता `2 /11 ` है तो, घटना 'A नहीं' की प्रायिकता ज्ञात कीजिए ।
View Solutionशब्द 'ASSASSINATION ' से एक अक्षर यादृच्छया चुना जाता है । प्रायिकता ज्ञात कीजिए कि चुना गया अक्षर (i ) एक स्वर है, (ii ) एक व्यंजन है।
View Solutionएक लॉटरी में एक व्यक्ति 1 से 20 तक कि संख्याओं में से 6 भिन्न-भिन्न संख्याओं का यादृच्छया चयन करता है और यदि यह चयनित उन 6 संख्याओं से मेल कहती है , जीने लॉटरी सिमित ने पूर्व निर्धारित कर रखा है तो वह व्यक्ति इनका जीत जाता है । लॉटरी के खेल में इनाम जितने कि प्रयिक्ता क्या है ?
View Solutionजांच कीजिए कि निम्न प्रायिकता `P (A )` तथा `P (B )` युक्तिसंगत (consistently ) परिभाषित की गई है :
`P(A)=0.5, P(B) =0.7, P(AnnB)=0.6`
View Solutionजांच कीजिए कि निम्न प्रायिकता `P (A )` तथा `P (B )` युक्तिसंगत (consistently ) परिभाषित की गई है :
`P(A)=0.5 , P(B) =0.4, P(AuuB)=0.8`
View Solutionसारणी में खाली स्थान भरिए-
`{:(P(A), P(B), P(AnnB), P (AuuB)),(1/3, 1/5, 1/15, ....):}`
View Solutionसारणी में खाली स्थान भरिए-
`{:(P(A), P(B), P(AnnB), P (AuuB)),(0.35, ...., 0.25, 0.6):}`
View Solutionसारणी में खाली स्थान भरिए-
`{:(P(A), P(B), P(AnnB), P (AuuB)),(0.5, 0.345, ...., 0.7):}`
View Solution`(A)=3/5` और `P(B)=1/5,` दिया गया है । यदि A और B परस्पर अपवर्जी घटनाएँ है तो P (A या B ) ज्ञात कीजिए ।
View Solutionघटनाएँ E और F इस प्रकार है कि P (E -नहींऔर F -नहीं) `=0.25,` बताइए कि E और P परस्पर अपवर्जी है या नहीं ।
View Solutionघटनाएँ A और B इस प्रकार है कि `P (A)=0.32, P (B)=0.48` P (A और B ) `=0.16` ज्ञात कीजिए-
P (A -नहीं)
View Solutionघटनाएँ A और B इस प्रकार है कि `P (A)=0.32, P (B)=0.48` P (A और B ) `=0.16` ज्ञात कीजिए-
P (B -नहीं)
View Solutionघटनाएँ A और B इस प्रकार है कि `P (A)=0.32, P (B)=0.48` P (A और B ) `=0.16` ज्ञात कीजिए-
P (A या B )
View Solutionएक आवेश परीक्षा कि दो परीक्षणों (Tests ) के आधार पर श्रेणीबद्ध किया जाया है। किसी यादृच्छया चुने गये विद्यार्थी की पहली परीक्षण में उत्तीर्ण होने की प्रायिकता `0।8` है और दूसरे परीक्षण में उत्तीर्ण होने की प्रायिकता `0.7` है । दोनों में कम-से-कम एक में उत्तीर्ण करने की प्रायिकता `0.95` है । दोनों परिश्नो को उत्तीर्ण करने की प्रायिकता क्या है ?
View Solutionएक विद्यार्थी के अंतिम परीक्षा के अंग्रेजी और हिंदी दोनों विषयो को उत्तीर्ण करने की प्रायिकता `0।5` है और दोनों में से कोई भी विषय उत्तीर्ण न करने की प्रायिकता `0.1` है। यदि अंग्रेजी की परीक्षा उत्तीर्ण करने की प्रयिक्ता `0.75` हो तो हिंदी की परीक्ष उत्तीर्ण करने की प्रायिकता क्या होगी ?
View Solutionएक कक्षा में 60 विद्यार्थियों में से 30 ने एन. सी. सी (NCC) 32 ने एन. एस. एस (NSS) और 24 ने दोनों को चुना है । यदि इनमे से एक विद्यार्थी यादृच्छया चुना गया है तो प्रायिकता ज्ञात कीजिए कि
विद्यार्थी ने एन. सी. सी या एन. एस. एस को चुना है।
View Solutionएक कक्षा में 60 विद्यार्थियों में से 30 ने एन. सी. सी (NCC) 32 ने एन. एस. एस (NSS) और 24 ने दोनों को चुना है । यदि इनमे से एक विद्यार्थी यादृच्छया चुना गया है तो प्रायिकता ज्ञात कीजिए कि
विद्यार्थी ने न तो एन.सी. सी और न ही एन.एस. एस को चुना है ।
View Solutionएक कक्षा में 60 विद्यार्थियों में से 30 ने एन. सी. सी (NCC) 32 ने एन. एस. एस (NSS) और 24 ने दोनों को चुना है । यदि इनमे से एक विद्यार्थी यादृच्छया चुना गया है तो प्रायिकता ज्ञात कीजिए कि
विद्यार्थी ने एन. एन. एस को चुना है किन्तु एन. सी. सी. को नहीं चुना है ।
View Solutionएक डिब्बे में 10 लाल , 20 नीली व 30 हरी गोलियाँ राखी है । डिब्बे में से 5 गोलियाँ यादृच्छया निकाली जाती है । प्रायिकता क्या है कि-
सभी गोलियाँ नीली है
View Solutionएक डिब्बे में 10 लाल , 20 नीली व 30 हरी गोलियाँ राखी है । डिब्बे में से 5 गोलियाँ यादृच्छया निकाली जाती है । प्रायिकता क्या है कि-
कम-से-कम एक गोली हरी है ?
View Solutionताश के पत्तो कि एक अच्छी तरह फेटी गई गड्डी में से 4 पत्ते निकले जाते है । इस बात कि क्या प्रयिक्ता है कि निकले गये पत्तो में 3 इट और एक हुकुम का पत्ता है ?
View Solutionएक लॉटरी में 10 , 000 टिकट बेचे गये जिसमे दस समान इनाम दिये जाने है । कोई भी इनाम न मिलने कि प्रयिक्ता क्या है ? यदि आप
एक टिकट खरीदते है
View Solutionएक लॉटरी में 10 , 000 टिकट बेचे गये जिसमे दस समान इनाम दिये जाने है । कोई भी इनाम न मिलने कि प्रयिक्ता क्या है ? यदि आप
दो टिकट खरीदते है
View Solutionएक लॉटरी में 10 , 000 टिकट बेचे गये जिसमे दस समान इनाम दिये जाने है । कोई भी इनाम न मिलने कि प्रयिक्ता क्या है ? यदि आप
10 टिकट खरीदते है ?
View Solution100 छात्रों में से 40 तथा 60 छात्रों के दो वर्ग बनाये गये है । यदी आप और आपका मित्र 100 छात्रों में है, तब प्रायिकता क्या है कि :
आप दोनों एक ही वर्ग में हो ?
View Solution100 छात्रों में से 40 तथा 60 छात्रों के दो वर्ग बनाये गये है । यदी आप और आपका मित्र 100 छात्रों में है, तब प्रायिकता क्या है कि :
आप दोनों अलग-अलग वर्ग में हो ?
View Solutionतीन व्यक्तियो के लिए तीन पत्र लिखवाये गये है और प्रत्येक के लिए पता लिखा एक लिफाफा है । पत्रों को यादृच्छया लिफाफो में इस प्रकार डाला गया है कि प्रत्येक लिफाफे में एक ही पत्र है। प्रायिकता ज्ञात कीजिए कि कम-से-कम एक पात्र अपने सही लिफाफे में डाला गया है ।
View SolutionA और B दो घटनाएँ इस प्रकार है कि `P (A)=0.54, P(B)=0.69` `P (AnnB)=0.35` ज्ञात कीजिए-
`P(AuuB)`
View SolutionA और B दो घटनाएँ इस प्रकार है कि `P (A)=0.54, P(B)=0.69` `P (AnnB)=0.35` ज्ञात कीजिए-
`P(A'nnB')`
View SolutionA और B दो घटनाएँ इस प्रकार है कि `P (A)=0.54, P(B)=0.69` `P (AnnB)=0.35` ज्ञात कीजिए-
`P(AnnB')`
View SolutionA और B दो घटनाएँ इस प्रकार है कि `P (A)=0.54, P(B)=0.69` `P (AnnB)=0.35` ज्ञात कीजिए-
`P (BnnA')`
View Solutionएक संस्था के कर्मचारियों में से 5 कर्मचारियों का चयन प्रबन्ध समिति के लिए किया गया है । पांच कर्मचारियों का ब्यौरा निम्नलिखित है-
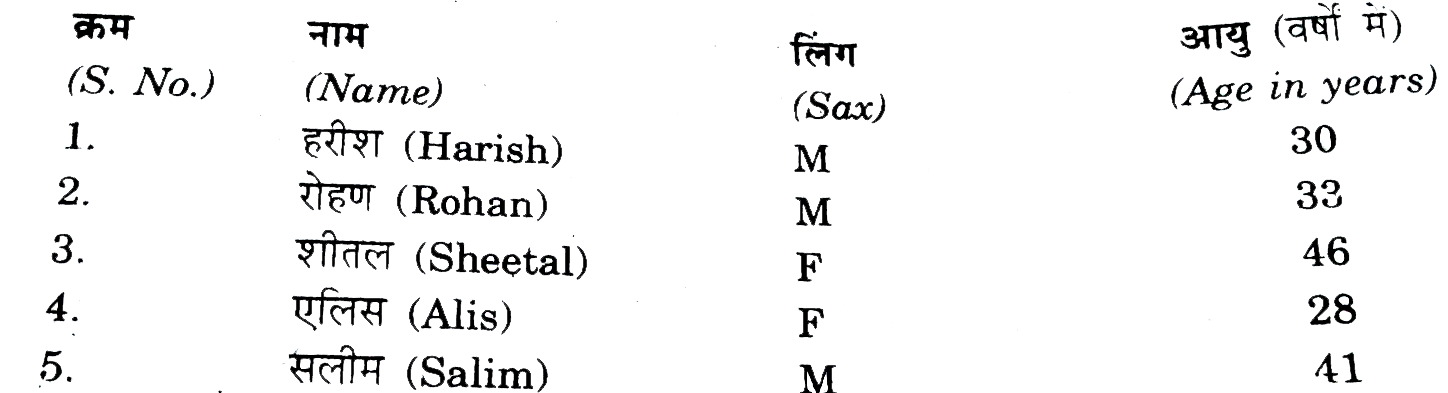
इस समूह से प्रवक्ता पद के लिए यादृच्छया एक व्यक्ति का चयन किया गया । प्रवक्ता के पुरुष या 35 वर्ष से अधिक आयु का होने कि प्रायिकता क्या है ?
View Solutionयदि `0,1,3,5` और 7 द्वारा `5,000` से बड़ी चार अंको कि संख्या का यादृच्छया निर्माण किया गया हो तो पांच से भाज्य संख्या के निर्माण कि क्या प्रायिकया है ।
अंको की पुनरावृत्ति नहीं की जाये।
View Solutionयदि `0,1,3,5` और 7 द्वारा `5,000` से बड़ी चार अंको कि संख्या का यादृच्छया निर्माण किया गया हो तो पांच से भाज्य संख्या के निर्माण कि क्या प्रायिकया है ।
अंको की पुनरावृत्ति की जाये ।
View Solutionकिसी अटेची के ताले में चार चक्र लगे है ।जिनमे प्रत्येक पर 0 से 9 तक 10 अंक अंकित है। ताला चार अंको के लिए विशेष क्रम (अंको की पुनरावृत्ति नहीं) द्वारा ही खुलता है । इस बात की क्या प्रायिकता है की कोई व्यक्ति अटेची खोलने के लिए सही क्रम का पता लगा ले ।
View Solutionएक पास के दो फलको में से प्रत्येक पर संख्या '1 ' अंकित है , तीन फलको में प्रत्येक पर संख्या '2 ' अंकित है और एक फलां पर संख्या '3 ' अंकित है । यदि पासा एक बार फेका जाता है तो ज्ञात कीजिए :
`P(2)`
View Solutionएक पास के दो फलको में से प्रत्येक पर संख्या '1 ' अंकित है , तीन फलको में प्रत्येक पर संख्या '2 ' अंकित है और एक फलां पर संख्या '3 ' अंकित है । यदि पासा एक बार फेका जाता है तो ज्ञात कीजिए :
P (1 या 3)
View Solutionएक पास के दो फलको में से प्रत्येक पर संख्या '1 ' अंकित है , तीन फलको में प्रत्येक पर संख्या '2 ' अंकित है और एक फलां पर संख्या '3 ' अंकित है । यदि पासा एक बार फेका जाता है तो ज्ञात कीजिए :
P (3नहीं )
View Solutionयदि E व F घटनाएँ इस प्रकार है कि `P(E)=1/4, P (F) =1/2` और P (E और E ) `=1/8,` तो ज्ञात कीजिए :
P (E या F )
View Solutionयदि E व F घटनाएँ इस प्रकार है कि `P(E)=1/4, P (F) =1/2` और P (E और E ) `=1/8,` तो ज्ञात कीजिए :
P (E -नहीं और F -नहीं) ।
View Solutionएक परीक्षण में पाए के एक जोड़े को फेकते है और उन पर प्रकट संख्याओं को लिखते है निम्नलिखत घटनाओ का वर्णन कीजिए :
A : प्राप्त संख्याओं का योग 8 से अधिक है ।
B : दोनों पासो पर संख्या 2 प्रकट होती है ।
C : प्रकट संख्याओं का योग कम-से-कम 7 है और 3 गुणज है ।
इस घटनाओ के कौन-कौन से युग्म परस्पर अपवर्जी है।
View Solution
एनसीईआरटी कॉर्नर questions and complete solutions for chapter प्रायिकता of गणित of Class 11