Complete Solutions to All Questions of chapter HYPERBOLA of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | HYPERBOLA |
| Mathematics | All Questions |
| Number Of Questions | 76 |
| Academic Year | 2023-24 |
Find the equation of the hyperbola whose foci are (8, 3) and (0, 3) and eccentricity is `4/3` .
View SolutionShow that the set all points such that the difference of their distances from `(4,0)a n d(-4,0)` is always equal to 2 represents a hyperbola.
View SolutionIf `ea n de '` the eccentricities of a hyperbola and its conjugate, prove that `1/(e^2)+1/(e '^2)=1.`
View SolutionFind the locus of the point of intersection of the lines `sqrt(3x)-y-4sqrt(3lambda)=0a n dsqrt(3)lambdax+lambday-4sqrt(3)=0` for different values of `lambdadot`
View SolutionShow that the equation 9`x^2-16 y^2-18 x+32 y-151=0` represents a hyperbola. Find the coordinates of the centre, lengths of the axes, eccentricity, latus-rectum, coordinates of foci and vertices, equations of the directrices of the hyperbola.
View SolutionFor the following hyperbolas find the lengths of transverse and conjugate axes, eccentricity and coordinates of foci and vertices, length of the latus-rectum, equations of the directrices: `6x^2-9y^2=144` `3x^2-6y^2=-18`
View Solution
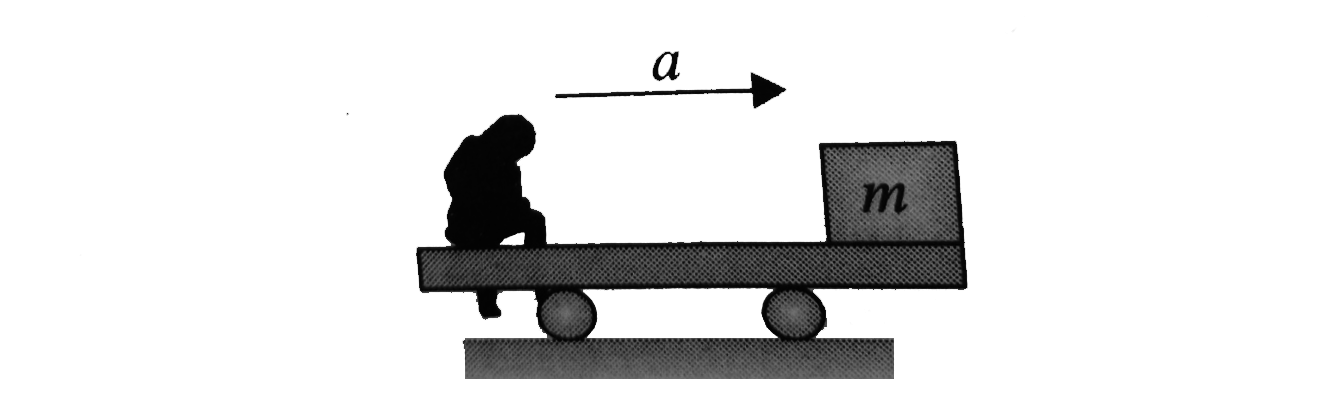
Suppose you are sitting on an accelrating trolley car.
(i) Find the pseudo force action on the block of mass m placed on the trolley car.
If the block is placed (or moved) outside the trolley car, and an external force F acts in horizontal direction.
(ii) Find the pseudo force acting on the block as viewed by the observer.
(iii) Find the acceleration of the block as seen by the obersever
View SolutionFind the equation of the hyperbola whose foci are `(6,4)a n d(-4,4)` and eccentricity is 2.
View SolutionFind the equation of the hyperbola, the length of whose latusrectum is 8 and eccentricity is `3//sqrt(5)dot`
View SolutionThe genes, which remains confined to differential region of Y-chromosome, are
View SolutionFind the equation of the hyperbola, referred to its principal axes of coordinates, in the following cases: `Vertices at(+-5,0),Foci at(+-7,0)` `V e r t i c e s a t(0,+-7), e=4/3`
View SolutionShow that the equation `x^2-2y^2-2x+8y-1=0` represents a hyperbola.
View SolutionIf `P` is any point on the hyperbola whose axis are equal, prove that `S PdotS^(prime)P=C P^2dot`
View SolutionFind the equation of the hyperbola whose conjugate axis is 5 and the distance between the foci is 13.
View SolutionThe foci of a hyperbola coincide with the foci of the ellipse `(x^2)/(25)+(y^2)/9=1.` Find the equation of the hyperbola, if its eccentricity is 2.
View SolutionIf the distance between the foci of a hyperbola is `16` and its eccentricity is `sqrt(2)` , then obtain its equation.
View SolutionThe equation of the directrix of a hyperbola is `x-y+3=0.` Its focus is (-1,1) and eccentricity 3. Find the equation of the hyperbola.
View SolutionFind the equation of the hyperbola whose : focus is (0,3) directrix is `x+y-1=0\ ` and eccentricity `=2.`
View SolutionFind the equation of the hyperbola whose : focus is (1,1) directrix is `3x+4y+8=0` and eccentricity `=2`
View SolutionFind the equation of the hyperbola whose : focus is (1,1) directrix is `2x+y=1` and eccentricity `=sqrt(3)`
View SolutionFind the equation of the hyperbola whose : focus is (2,-1) directrix is `2x+3y=1` and eccentricity `=2`
View SolutionFind the equation of the hyperbola whose : focus `(a ,0)` , directrix is `2x-y+a=0\ ` and eccentricity`\ =4/3\ `
View SolutionFind the equation of the hyperbola whose : focus is (2,2) directrix is `x+y=9` and eccentricity `=2.`
View SolutionFind the eccentricity, coordinates of the foci ,equations of directrices and length of the latus rectum of the hyperbola :`9x^2-16 y^2=144`
View SolutionFind the eccentricity, coordinates of the foci, equations of directrices and length of the latus rectum of the hyperbola `4x^2-3y^2=36`
View SolutionFind the eccentricity, coordinates of the foci ,equations of directrices and length of the latus rectum of the hyperbola `2x^2-3y^2=5.`
View SolutionFind the eccentricity, coordinates of the foci, equations of directrices and length of the latus rectum of the hyperbola `16 x^2-9y^2=144`
View SolutionFind the eccentricity, coordinates of the foci, equations of directrices and length of the latus rectum of the hyperbola `3x^2-y^2=4`
View SolutionFind the axes, eccentricity, latus rectum and the coordinates of the foci of the hyperbola `25 x^2-36 y^2=225.`
View SolutionFind the centre, eccentricity, foci and directrices of the hyperbola : `16 x^2-9y^2+32 x+36 y-164=0`
View SolutionFind the centre, eccentricity, foci and directrices of the hyperbola : `x^2-y^2+4x=0`
View SolutionFind the centre, eccentricity, foci and directrices of the hyperbola : `x^2-3y^2-2x=8.`
View SolutionFind the equation of the hyperbola, referred to its principal axes as axes of coordinates in the following cases: a. The distance between the foci `=16` and eccentricity `=sqrt(2)` b. Conjugate axis is 5 and the distance between foci `=3` c. Conjugate axis is 7 and passes through the point (3,-2).
View SolutionFind the eccentricity of the hyperbola, the length of whose conjugate axis is `3/4` of the length of transverse axis.
View SolutionFind the equation of the hyperbola whose: focus is at (5,2) vertex at (4,2) and centre at (3,2)
View SolutionFind the equation of the hyperbola whose: focus is at (4,2) and centre at (6,2) , e=2.
View SolutionIn each of the following find the equations of the hyperbola satisfying the given condition: Vertices `(+-2,0),\ foc i(+-3,0)`
View SolutionFind the equations of the hyperbola satisfying the given conditions :Vertices `(0,+-5),f o c i (0,+-8)`
View SolutionIn each of the following find the equations of the hyperbola satisfying he given condition: vertices `(0,+-3)foc i\ (0,+-5)`
View SolutionIn each of the following find the equations of the hyperbola satisfying he given condition: foci `(+-5,0)` transverse axis `=8`
View SolutionIn each of the following find the equations of the hyperbola satisfying he given condition: `foc i\ (0,+-13)` conjugate axis `=24`
View SolutionIn each of the following find the equations of the hyperbola satisfying the given condition: `foc i\ (+-3sqrt(5),0)`, the latus rectum `=8`
View SolutionIn each of the following find the equations of the hyperbola satisfying the given condition: `foc i\ (+-4,0)` the latus rectum `=12`
View SolutionIn each of the following find the equations of the hyperbola satisfying the given condition: vertices `(0,+-6),\ e=5/3`
View SolutionIn each of the following find the equations of the hyperbola satisfying the given condition: foci `(0,+-sqrt(10))` passing through (2,3)
View SolutionIn each of the following find the equations of the hyperbola satisfying the given condition: foci `(0,+-12)` latus rectum`=36`
View SolutionWrite the eccentricity of the hyperbola `9x^2-16 y^2=144.`
View SolutionFind the eccentricity of the hyperbola whose latusrectum is half of its transverse axis.
View SolutionWrite the coordinates of the foci of the hyperbola `9x^2-16 y^2=144.`
View SolutionWrite the equation of the hyperbola of eccentricity `sqrt(2)` if it is known that the distance between its foci is 16.
View SolutionIf the foci of the ellipse `(x^2)/(16)+(y^2)/(b^2)=1` and the hyperbola `(x^2)/(144)-(y^2)/(81)=1/(25)` coincide write the value of `b^2dot`
View SolutionWrite the length of the latus rectum of the hyperbola `16 x^2-9y^2=144.`
View SolutionIf the latus rectum through one focus subtends a right angle at the farther vertex of the hyperbola then its eccentricity is
View SolutionWrite the distance between the directrices of the hyperbola `x=8s e ctheta,\ y=8t a nthetadot`
View SolutionWrite the equation of the hyperbola whose vertices are `(+-3,0)` and foci at `(+-5,0)`
View SolutionIf `e_1a n d\ e_2` are respectively the eccentricities of the ellipse `(x^2)/(18)+(y^2)/4=1` and the hyperbola `(x^2)/9-(y^2)/4=1,` then write the value of `2e_1^ 2+e_2^ 2dot`
View SolutionEquation of the hyperbola whose vertices are `(+-3,0)` and foci at `(+-5,0)` is a.`16 x^2-9y^2=144` b. `9x^2-16 y^2=144` c. `25 x^2-9y^2=225` d. `9x^2-25 y^2=81`
View SolutionIf `e_1a n d\ e_2` are respectively the eccentricities of the ellipse `(x^2)/(18)+(y^2)/4=1` and the hyperbola `(x^2)/9-(y^2)/4=1,` then the relation between `e_1a n d\ e_2` is a.`2e_1 ^2+e_2 ^2=3` b. `e_1 ^2+2e_2^ 2=3` c. `2e_1^ 2+e_2 ^2=3` d. `e_1 ^2+3e_2 ^2=2`
View SolutionThe distance between the directrices of the hyperbola `x=8s e ctheta,\ y=8\ t a ntheta,` a.`8sqrt(2)` b. `16sqrt(2)` c. `4sqrt(2)` d. `6sqrt(2)`
View SolutionThe equation of the conic with focus at (1,-1) directrix along `x-y+1=0` and eccentricity `sqrt(2)` is a.`x y=1` b. `2x y+4x-4y-1=0` c. `x^2-y^2=1` d. `2x y-4x+4y+1=0`
View SolutionThe eccentricity of the conic `9x^2-16 y^2=144` is a.`5/4` b. `4/3` c. `4/5` d. `sqrt(7)`
View SolutionA point moves in a plane so that its distance PA and PB from who fixed points A and B in the plane satisfy the relation `P A-P B=k(k!=0)` then the locus of `P` is a. a hyperbola b. a branch of the locus of `P` is c. a parabola d. an ellipse
View SolutionThe eccentricity of the hyperbola whose latus rectum is half of its transverse axis is a.`1/(sqrt(2))` b. `sqrt(2/3)` c. `sqrt(3/2)` d. none of these
View SolutionThe eccentricity of the hyperbola `x^2-4y^2=1` is a.`(sqrt(3))/2` b. `(sqrt(5))/2` c. `2/(sqrt(3))` d. `2/(sqrt(5))`
View SolutionThe difference of the focal distances of anypoint on the hyperbola is equal to a. Length of the conjugate axis b. Eccentricity c. Length of the transverse axis d. Latus rectum
View SolutionThe foci of the hyperbola `9x^2-16 y^2=144` are a.`(+-4,0)` b. `(0,+-4)` c. `(+-5,0)` d. `(0,+-5)`
View SolutionThe distance between the foci of a hyperbola is 16 and its eccentricity is `sqrt(2)` then equation of the hyperbola is a.`x^2+y^2=32` b. `x^2-y^2=16` c. `x^2+y^2=16` d. `x^2-y^2=32`
View SolutionIf `e_1` is the eccentricity of the conic `9x^2+4y^2=36\ a n d\ e_2` is the eccentricity of the conic `9x^2-4y^2=36` then a. `e_1 ^2-e_2^ 2=2` b. `e_2 ^2-e_1 ^2=2` c. 2< `e_2^2-e_1^2<3` d.`e_1^2-e_2^2>3`
View SolutionIf the eccentricity of the hyperbola `x^2-y^2sec^2alpha=5\ i s\ sqrt(3)` times the eccentricity the ellipse `x^2sec^2alpha+y^2=25\ t h e n\ alpha=` a.`pi/6` b. `pi/4` c. `pi/3` d. `pi/2`
View SolutionThe equation of the hyperbola whose foci are (6,4) and (-4,4) and eccentricity 2 is a.`((x-1)^2)/(25//4)-((y-4)^2)/(75//4)=1` b. `((x+1)^2)/(25//4)-((y+4)^2)/(75//4)=1` c. `((x-1)^2)/(75//4)-((y-4)^2)/(25//4)=1` d. none of these
View SolutionThe length of the straight line `x-3y=1` intercepted by the hyperbola `x^2-4y^2=1` is a.`6/(sqrt(5))` b. `3sqrt(2/5)` c. `6sqrt(2/5)` d. none of these
View SolutionThe latus rectum of the hyperbola `16 x^2-9y^2=144` is a.`16//3` b. `32//3` c. `8//3` d. `4//3`
View SolutionThe foci of the hyperbola `2x^2-3y^2=5` are a.`(+-5sqrt(6),0)` b. `(+-5//6,0)` c. `(+-sqrt(5)//6,0)` d. none of these
View SolutionThe eccentricity of the hyperbola `x=a/2(t+1/t), y=a/2(t-1/t)` is a.`sqrt(2)` . b. `sqrt(3)` c. `2sqrt(3)` d. `3sqrt(2)`
View SolutionThe equation of the hyperbola whose centre is `(6,2)` one focus is `(4,2)` and of eccentricity 2 is (A) `3(x-6)^2-(y-2)^2=3` (B) `(x-6)^2-3(y-2)^2=1` (C) `(x-6)^2-2(y-2)^2=1` (D) `2(x-6)^2-(y-2)^2=1`
View SolutionThe locus of the point of intersection of the lines `sqrt(3)x-y-4sqrt(3)lambda=0\ a n d\ sqrt(3)lambdax+lambday-4sqrt(3)=0` is a hyperbola of eccentricity a.`1` b. `2` c. `3` d. `4`
View Solution
All Questions questions and complete solutions for chapter HYPERBOLA of RD SHARMA MATHS (ENGLISH) of Class 11