Complete Solutions to All Questions of chapter THE STRAIGHT LINES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | THE STRAIGHT LINES |
| Mathematics | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Show that the straight lines given by `(2+k)x+(1+k)y=5+7k` for different values of `k` pass through a fixed point. Also, find that point.
View SolutionFind the equation of the internal bisector of `angle B A C` of the `triangle A B C` whose vertices `A ,` `B,` `C` are`(5,2),` `(2,3)` and `(6,5)` respectively.
View SolutionThe ratio in which the line segment joining (-1,1) and (5,7) is divided by the line `x+y=4` is
View SolutionThe mid points of the sides of a triangle are (2,1), (-5,7) and (-5,-5).The equation of sides are : (A) x-2=0 (B) 6x+7y+65=0 (C) 6x-7y+79=0 (D) All of these
View SolutionFind the equation of the altitudes of the triangle whose vertices are `A(7,-1),B(-2,8)a n dC(1,2)dot`
View SolutionOne side of a square makes an angle `alpha` with x axis and one vertex of the square is at origin. Prove that the equations of its diagonals are `x(sin alpha+ cos alpha) =y (cosalpha-sinalpha)` or `x(cos alpha-sin alpha) + y (sin alpha + cos alpha) = a`, where a is the length of the side of the square.
View SolutionShow that the perpendicular drawn from the point `(4,1)` on the line segment joining `(6,5)a n d(2,-1)` divides it internally in the ratio `8: 5.`
View SolutionProve that the perpendicular drawn from the point `(4,1)` on the join of`(2,-1)a n d(6,5)` divides it in the ratio `5: 8.`
View SolutionA line passing through the point `A(3,0)` makes `30^0` angle with the positive direction of x- axis . If this line is rotated through an angle of `15^0` in clockwise direction, find its equation in new position.
View SolutionIn what ratio is the line joining the points `(2,3)a n d(4,1)` divides the segment joining the points`(1,2)a n d(4,3)?`
View SolutionFind the equations to the altitudes of the triangle whose angular points are `A(2,-2),B(1,1)a n dC(-1,0)dot`
View SolutionFind the equations of the diagonals of the square formed by the lines `x=o,y=0,x=1a n dy=1.`
View SolutionFind the equation of a line which cuts off intercepts `a ` and ` b` respectively from the `x` and `y-a x e s`.
View SolutionFind the equation of the bisector of angle `A` ofthe triangle whoe vertices are `A(4,3),B(0,0)a n d C(2,3)dot`
View SolutionFind the equations of the straight lines which go through the origin and trisect the portion of the straight line `3x+y=12` which is intercepted between the axes of coordinates.
View SolutionA line L is such that its segment between the straight lines 5x - y - 4 = 0 and 3 x + 4y - 4 = 0 is bisected at the point (1,5) . Obtain the equation.
View SolutionFind the equations to the diagonals of the rectangle the equations of whose sides are `x=a ,x=a^(prime),y=b ` `a n d ` `y=b^(prime)`
View SolutionA rectangle has two opposite vertices at the points `(1,2)` `a n d` `(5,5)`. If the other vertices lie on the line `x=3` , find the equations of the sides of the rectangle.
View SolutionFind the coordinates of the vertices of `a` square inscribed in the triangle with vertices `A(0,0),B(3,0) a n d C(2,1);` given that two of its vertices are on the side `A Bdot`
View SolutionIf the intercept of a line between the coordinate axes is divided by the point `(-5,4)` in the ratio `1:2,` then find the equation of the line.
View SolutionA straight line moves so that the sum of the reciprocals of its intercepts made on axes is constant. Show that the line passes through a fixed point.
View SolutionFind the equations of lines parallel to `3x-4y-5=0` at a unit distance from it.
View SolutionIf the length of the perpendicular from the point `(1,1)` to the line `a x-b y+c=0` be unity, show that `1/c+1/a-1/b=c/(2a b)`
View SolutionIf `t_1 a n d t_2` are roots of eth equation `t^2+lambdat+1=0,` where `lambda` is an arbitrary constant. Then prove that the line joining the points `(a t1,22a t_1)a d n(a t2,22a t_2)` always passes through a fixed point. Also, find the point.
View SolutionShow that the locus of the mid-point of the segment intercepted between the axes of the variable line `xcosalpha+ysinalpha = p` then `1/(x^2)+1/(y^2)=4/(p^2),` where `p` is a constant.
View SolutionFind the equation of the line which passes through `P(1,-7)` and meets the axes at A and B respectively so that `4A P-3B P=0.`
View SolutionThe area of the triangle formed by the coordinates axes and a line is `6` square unit length of d a line is 6 square units a tie'hypotenuse is `5` units. Find the equation of the line.
View SolutionFind the equations of the line which passes through the point `(3,4)` and the sum of its intercepts on the axes is `14` .
View SolutionFor what values of `aa n db` the intercepts cut off n the coordinate axes by the line `a x+b y+8=0` are equal in length but opposite in signs to those cut off by the line `2x-3y+6=0` on the axes.
View SolutionFind the equation of the straight line which passes though `(1,-2)a n d` cuts off equal intercepts on the axes.
View SolutionIf the line `(x/a)+(y/b)=1` moves in such a way that `(1/(a^2))+(1/(b^2))=(1/(c^2))` , where `c` is a constant, prove that the foot of the perpendicular from the origin on the straight line describes the circle `x^2+y^2=c^2dot`
View SolutionIf the sum of the distances of a moving point in a plane from the axes is `1,` then find the locus of the point.
View SolutionFind the equation of the straight lines each of which passes through the point `(3,2)` and cuts off intercepts a and b respectively on x and y - axes such that `a-b=2.`
View SolutionThe equation of straight line which passes through the point (-4,3) such that the portion of the line between the axes is divided by the point in ratio 5:3 is -
View SolutionProve that the length of perpendiculars from points 'P(m^2,2m) Q (mn ,m+n) and R(n^2,2n)' to the line `x cos^2theta+ysinthetacostheta+sin^2theta=0` are in G.P.
View SolutionThe equation of the base of an equilateral triangle is `x+y-2=0` and the opposite vertex has coordinates (2, -1). Find the area of the triangle.
View SolutionFind the equations of lines passing through the point `(1,0)` and a distance `(sqrt(3))/2` from the origin.
View SolutionFind the coordinates of a point on `x+y+3=0,` whose distance from `x+2y+2=0` is `sqrt(5)dot`
View SolutionA point moves such teat its distance from the point `(4,0)` is half that of its distance from the line `x=16 ,` find its locus.
View SolutionFind the locus of a point which moves in such away that the square of its distance from the point `(3,-4)` is numerically equal to its distance from the line `5x-12 y=13.`
View SolutionFind the equation of the straight line on which the length of the perpendicular from the origin is `4` units and the line makes an angle of `120^0` with positive direction of x-axis
View SolutionFind the equation of the straight line upon which the length of the perpendicular from the origin is `5a n d` the slope of this perpendicular is `3/4dot`
View SolutionA line forms a triangle of area `54sqrt(3)s q u a r e` units with the coordinate axes. Find the equation of the line if the perpendicular drawn from the origin to the line makes an angle of `60^0` with the X-axis.
View SolutionA straight canal is `4 1/2m i l e s` from a place and the shortest route from this place to the canal is exactly north-east. A village is `3m i l e s` north and four miles east from the place. Does it lie by the nearest edge of the canal?
View SolutionFind the equation of the line on which the length of the perpendicular segment from the origin to the line is `4` and the inclination of the perpendicular segment with the positive direction of x axis is`30^0dot`
View SolutionFind the equation of the straight line on which the length of the perpendicular from the origin is `2` and the perpendicular makes an angle `alpha` with x-axis such that `sinalpha=1/3dot`
View SolutionFind the equation of a straight line on which the perpendicular from the origin makes an angle of `30^0` with x-axis and which forms a triangle of area `50sqrt(3)` with the axes.
View SolutionThe slope of a straight line through `A(3,2)i s3//4` Find the coordinates of the points on the line that are `5u n i t s` away from`Adot`
View SolutionFind the equation of the line through the point `A(2,3)` and making an angle an angle of `45^0` with the x-a xi s . Also, determine the length of intercept on it between `A a n d` the line `x+y+1=0.`
View SolutionIf the straight line through the point (3,4) makes an angle `pi/6` with x-axis and meets the line 12 x + 5 y + 10 = 0 at Q, Then the length of PQ is :
View SolutionThe angle between the diagonals of a quadrilateral formed by the lines `x/a+y/b=1,x/b+y/a=1,x/a+y/b=2 and x/b+y/a=2` is
View SolutionFind the equation of two straight lines which are parallel to `x+7y+2=0` and at unit distance from the point `(1,-1)dot`
View SolutionShow that the lines `4x+y-9=0,x-2y+3=0,5x-y-6=0` make equal intercepts on any line of slope 2.
View SolutionFind the value of `m` for which the lines `m x+(2m+3)y+m+6=0a n dm x+(2m+1)x+(m-6)y+9=0` intersect at a; point on `y-a xi sdot`
View SolutionThe sides `A Ba n dA C` of a triangle `A B C` are respectively `2x+3y=29a n dx+2y=16` respectively. If the mid-point of `B Ci s(5,6)` then find the equation of `B Cdot`
View SolutionA line through `A(-5,-4)` meets the lines `x+3y+2=0,2x+y+4=0 and x-y-5=0` at the points `B , Ca n dD` rspectively, if `((15)/(A B))^2+((10)/(A C))^2=(6/(A D))^2` find the equation of the line.
View SolutionExplain BPT Theorem
View SolutionTransform the equation of the line `sqrt(3)x+y-8=0` to (i) slope intercept form and find its slope and y-intercept (ii) intercept form and find intercepts in the coordinates axes (iii) normal form and find the inclination of the perpendicular segment from the origin on the line with the axis and its length.
View SolutionFind the distance of the point `(2,3)` from the line `2x-3y+9=0` measured along a line `x-y+1=0.`
View SolutionThe line joining two points A(2,0) and B(3,1) is rotated about A in anticlockwise direction through an angle of `15^@`. find the equation of line in the new position. If b goes to c in the new position what will be the coordinates of C.
View SolutionFind the direction in which a straight line must be drawn through the point `(1,2)` so that its point of intersection with the line `x+y" = "4` may be at a distance of 3 units from this point.
View SolutionShow that the equations of the straight lines passing through the point `(3,-2)` and inclined at `60^0` to the line `sqrt(3)x+y=1 a r e y+2=0a n dy-sqrt(3)x+2+3sqrt(3)=0.`
View SolutionA vertex of an equilateral triangle is `(2,3)` and the opposite side is `x+y=2.` Find the equations of other sides.
View SolutionFind the value of `lambda` , if the line `3x-4y-13=0,8x-11 y-33=0 `and `2x-3y+lambda=0` are concurrent.
View SolutionIf the lines `a x+y+1=0,x+b y+1=0` and `x+y+c=0` are concurrent `(a!=b!=c!=1)` , prove that `1/(1-a)+1/(1-b)+1/(1-c)=1` .
View SolutionIf the straight line `x/a+y/b=1` passes through the line point of intersection of the lines `x+y=3` and `2x-3y=1` and is parallel to `x-y-6=0` , find `a` and `b. `
View SolutionFind the orthocentre of the triangle the equations of whose sides are `x+y=1,2x+3y=6a n d4x-y+4=0.`
View SolutionTwo vertices of a triangle are `(3,-1)a n d(-2,3)` and its orthocentre is at the origin,. Find the coordinates of its third vertex.
View SolutionTwo consecutive sides of a parallelogram are `4x+5y=0` and `7x+2y=0.` If the equation of one diagonal is `11 x+7y=9,` Equation of other diagonal : (A) `11x + 7y =0` (B) `3x - 5y + 5 = 0` (C) `7x + 11y = 0` (D) `x-y =0`
View SolutionFind the equation of the straight line passing through the point of intersection of the lines `5x-6y-1=0` and `3x+2y+5=0` and perpendicular to the line `3x-5y+11=0.`
View SolutionShow that the line `x-y-6=0,4x-3y-20=0` and `6x+5y+8=0` are concurrent. Also, find their common point of intersection.
View SolutionThree sides `A B ,A Ca n dC A` of triangle `A B C` are`5x-3y+2=0,x-3y-2=0a n dx+y-6=0` respectively. Find the equation of the altitude through the vertex `Adot`
View SolutionFind the coordinates of the incentre and centroid of the triangle whose sides have the equations `3x-4y=0,5 x+12y=0 and y-15=0.`
View SolutionShow that the straight lines given by `x(a+2b)+y(a+3b)=a` for different values of a and b pass through a fixed point.
View SolutionIf `a ,b ,c` are variables such that `3a+2b+4c=0` , then show that the family of lines givenby `a x+b y+c=0` pass through a fixed point. Also, find that point.
View SolutionIf the algebraic sum of the perpendiculars from the points `(2,0),(0,2),(1,1)` to a variable line be zero, then prove that line passes through a fixed-point whose coordinates are `(1,1)dot`
View SolutionA ray of light is sent along the line `x-2y-3=0` upon reaching the line `3x-2y-5=0,` the ray is reflected from it. Find the equation of the line containing the reflected ray.
View Solutionlines `L_1:ax+by+c=0` and `L_2:lx+my+n=0` intersect at the point `P` and make a angle `theta` between each other. find the equation of a line `L`different from `L_2` which passes through `P` and makes the same angle `theta` with `L_1`
View SolutionFind the equation of the straight line passing through the point of intersection of `2x+3y+1=0a n d3x-5y-5=0` and equally inclined to the axes.
View SolutionFind the equation of the straight line which cuts off intercept on X-axis which is twice that on Y-axis and is at a unit distance from the origin.
View SolutionFind the equation of the straight line passing through the point of intersection of `2x+y-1=0` and `x+3y-2=0` and making with the coordinate axes a triangle of area 3/8 sq. units.
View SolutionFind the equations of the lines through the point of intersection of the lines `x -y+1=0` and` 2x-3y+5= 0`whose distance from the point`(3, 2)` is `7/5`
View SolutionIf the diagonals of the quadrilateral formed by lines `l_1x+m_1y+n_1=0,` `l_2x+m_2y+n_2=0,` `l_1x+m_1y+n_1'=0,` and `l_2x+m_2y+n_2'=0,` are perpendicular, then value of `l_1^2-l_2^2+m_1^2-m_2^2.`
View SolutionWrite the area of the figure formed by the lines `a|x|+b|y|+c=0.`
View SolutionIf `theta` is the acute angle between the lines with slopes m1 and m2 then `tantheta = (m_1 -m_2)/(1+m_1m_2)`.If p is the length the perpendicular from point P(x1, y1) to the line ax+ by +c =0 then p= `(ax_1+by_1+c)/(sqrt(a^2+b^2))`
View SolutionA straight line `L` is perpendicular to the line `5x-y=1.` The area of the triangle formed by the line `L` and the coordinate axes is `5' square units. Find the equation of the line `L`
View SolutionFind the image of the point `(-8,12)` with respect to line mirror `4x+7y+13=0.`
View SolutionShow that the equation of a line passing through `(acos^3theta,asin^3theta)` and perpendicualar to the line `xsectheta+ycos e ctheta=a 'i s 'xcostheta-ysintheta-acos2thetadot`
View SolutionFind the equation of a straight line parallel to `2x+3y+11=0` and which is such that the sum of its intercepts on the axes is `15.`
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point `(1,-2)` on the line `y=2x+1.`
View SolutionIf the lines `p_1x+q_1y=1,p_2x+q_2y=1a n dp_3x+q_3y=1,` be concurrent, show that the point `(p_1, q_1),(p_2, q_2)a n d(p_3, q_3)` are collinear.
View SolutionProve that the medians of a triangle are concurrent and find the position vector of the point of concurrency (that is, the centroid of the triangle)
View SolutionShow that the altitudes of a triangle are concurrent
View SolutionTwo sides of an isosceles triangle are given by the equations `7x-y+3=0 and x+y-3=0` and its third side passes through the point `(1,-10)dot` Determine the equation of the third side.
View Solution
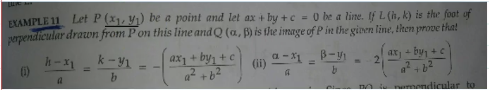
View SolutionFind the equations of the sides of an isosceles right angled triangle the equation of whose hypotenuse is `3x+4y=4` and the opposite vertex is the point (2, 2).
View SolutionA line `4x+y=1` passes through the point A(2,-7) and meets line BC at B whose equation is `3x -4y +1=0`, the equation of line AC such that `AB=AC` is (a) 52x +89y +519=0(b) 52x +89y-519=0 c) 82x +52y+519=0 (d) 89x +52y -519=0
View SolutionOne side of a rectangle lies along the line `4x+7y+5=0.` Two of its vertices are `(-3,1)` `a n d` `(1,1)dot` Find the equations of the other three sides.
View SolutionIf two opposite vertices of square are (1,2) and (5,8), find the coordinates of its other two vertices and the equations of its sides.
View SolutionFind the equation of the straight line which passes through the intersection of the lines `x-y-1=0` `a n d` `2x-3y+1=0` and parallel (i) `x`-axis (ii)`y`-axis (iii) 3x+4y=14.`
View Solution
All Questions questions and complete solutions for chapter THE STRAIGHT LINES of RD SHARMA MATHS (ENGLISH) of Class 11