Complete Solutions to All Questions of chapter TRIGONOMETRIC FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | TRIGONOMETRIC FUNCTIONS |
| Mathematics | All Questions |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
Prove that: `("cos"(2pi+theta)"c o s e c"(2pi+theta)"tan"(pi//2+theta))/("sec"(pi//2+theta)costheta"cot"(pi+theta))=1`
View SolutionProve that: `(sin(180^0+theta)cos(90^0+theta)t a n(270^0-theta)cot(360^0-theta))/(sin(360^0-theta)cos(360^0+theta)cos e c(-theta)"sin"(270^0+theta))=1`
View SolutionProve that: `(cos e c(90^0+theta)+cot(450^0+theta))/(cos e c(90^0-theta)+t a n(180^0-theta))+(t a n(180^0+theta)+s e c(180^0-theta))/(t a n(360^0+theta)-s e c(-theta))`=2
View SolutionProve that: `(t a n(90^0-theta)s e c(180^0-theta)sin(-theta))/(sin(180^0+theta)cot(360^0-theta)cosec(90^0-theta))=1`
View SolutionProve that: `{1+cottheta-s e c(pi/2+theta)}{1+cottheta+s e c(pi/2+theta)}=2cottheta`
View SolutionProve that: `2sin^2(3pi/4)+2cos^2(pi/4)+2sec^2(pi/3)=10`
View SolutionProve that: `sin^2(pi/6)+cos^2(pi/3)-t a n^2pi/4=-1/2`
View Solution`cot^2` `pi/6` `+cose c` `(5pi)/6` `+3tan^2` `pi/6=6`
View SolutionProve that: `2sin^2(pi/6)+cosec^2((7pi)/6)cos^2(pi/3)=3/2`
View SolutionFind all other trigonometrical ratios if ` sintheta=-(2sqrt(6))/5 andtheta` lies in quadrant III.
View SolutionFind `sinthetaa n dt a nthetaifcostheta=-(12)/(13)andtheta` lies in the third quadrant.
View SolutionIf `(sinA)/(sinB)=pa n d(cosA)/(cosB)=q ,` find `tanAa n dtanBdot`
View SolutionIf `10sin^4alpha+15cos^4alpha=6` , find the value of `27cos e c^6alpha+8s e c^6alpha` .
View SolutionIf `a=s e ctheta-t a ntheta` and `b=cos e ctheta+cottheta` , then show that `a b+a-b+1=0.`
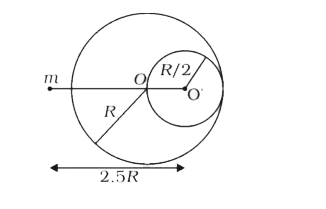
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
View SolutionIf `T_n=sin^ntheta+cos^ntheta` , prove that (i) `(T_3-T_5)/(T_1)=(T_5-T_7)/(T_3)` (ii) `2T_6-3T_4+1=0` (iii) `6T_(10)-15 T_8+10 T_6-1=0`
View SolutionProve that: `sqrt((1-sintheta)/(1+s intheta))+sqrt((1+sintheta)/(1-s intheta)=){2/(costheta),if0lt=theta
View SolutionIf `sectheta+tantheta=p ,` obtain the values of `sectheta,tantheta and sintheta` in terms of `p` .
View SolutionIf `acos theta-b sin theta=c ,` show that `asin theta+b cos theta=+-sqrt(a^2+b^2-c^2dot)`
View SolutionIf `t a ntheta+sintheta=m` and `tantheta-sintheta=n ,` show `m^(2)-n^2=4sqrt(m ndot)`
View SolutionProve that: `s e c^2theta+cos e c^2thetageq4` .
View SolutionGiven that: `(1+cosalpha)(1+cosbeta)(1+cosgamma)=(1-cosalpha)(1-cosbeta)(1-cosgamma)dot` Show that one of the values of each member of this equality is `sinalphasinbetasingammadot`
View SolutionProve that: `3(sintheta-costheta)^4+6(sintheta+costheta)^2+4(sin^6theta+cos^6theta)-13=0.`
View SolutionProve that: `2s e c^2theta-s e c^4theta-2cos e c^2theta+cos e c^4theta=(1-t a n^8theta)/(t a n^4theta)`
View SolutionIf `A` lies in second quadrant and `3tanA+4=0,` then the value of `2cotA-5cos A+sinA` is equal to
View SolutionIs the following inequality correct? `sin1^0> sin1`
View SolutionIf `f(x)=cos^2x+s e c^2x ,t h e n` (a) `f(x)<1` (b) `f(x)=1` (c) `2ltf(x)<1` (d) `""""f(x)ge2`
View SolutionIf `sectheta=x+1/(4x),` then `s e ctheta+t a ntheta=` (a) `x ,1/x` (b) `2x ,1/(2x)` (c) `-2x ,1/(2x)` (d) `-1/x ,x`
View SolutionIf `s e c^2theta=(4x y)/((x+y)^2)` is true if and only if (a)`x+y!=0` (b) `x=y , x!=0` (c) `x=y` (d) `x!=0,y!=0`
View SolutionIf `cos e ctheta+cottheta=(11)/2` , then `t a ntheta=` `(21)/(22)` (b) `(15)/(16)` (c) `(44)/(117)` (d) `(117)/(44)`
View SolutionIf `(3pi)/4 lt alpha lt pi`, then `sqrt(2cotalpha+1/(sin^2alpha))` is equal to (a) `1-cotalpha` (b) `1+cotalpha` (c) `-1+cotalpha` (d) `-1-cotalpha`
View SolutionIf `x=rsinthetacosphi,y=rsinthetasinphi and z=rcostheta, then x^2+y^2+z^2` is independent of `(a)theta,phi` (b) `r ,theta` (c) `r ,phi` (d) r
View SolutionIf `sintheta+costheta=0 and theta` lies in the fourth quadrant, find `sintheta and costheta`
View SolutionProve that: `sqrt(1-sintheta)/(1+s intheta)+sqrt((1+sintheta)/(1-s intheta)=){2/(costheta),if0lt=theta
View SolutionProve that: `cos((3pi)/2+x)cos(2pi+x){cot((3pi)/2-x)+"cot"(2pi+x)}=1`
View SolutionProve that: `(cos(pi+x)cos(-x))/(sin(pi-x)cos(pi/2+x)} =cot^2x`
View SolutionIf `x=(2sintheta)/(1+costheta+sintheta)` , then prove that `(1-costheta+sintheta)/(1+sintheta)` is equal to `x` .
View SolutionIf `tanx=(b)/(a)`, then find the value of `sqrt((a+b)/( a-b ))+sqrt((a-b)/(a+b)).`
View SolutionFind the values of the following trigonometric ratios. (1) `cos e c390^0` (ii) `cot570^0` (iii) `t a n480^0` (iv) `cos270^0` (v) `t a n(19pi)/3` (vi) `s in((-11pi)/3)` (vii) `cot(-15pi)/4`
View SolutionProve that: `sin(-420^0)(cos390^0)+cos(-660^0)(sin330^0)=-1.`
View SolutionProve that: `"sec"((3pi)/2-theta)"sec"(theta-(5pi)/2)+t a n((5pi)/2+theta)"tan"(theta-(3pi)/2)=-1.`
View SolutionProve that: `sin^2pi/(18)+sin^2pi/9+sin^2(7pi)/(18)+sin^2(4pi)/9=2`
View SolutionIf any quadrilateral ABCD, prove that `"sin"(A+B)+sin(C+D)=0` `"cos"(A+B)=cos(C+D)`
View SolutionFind the value of the expression `3{sin^4((3pi)/2-theta)+sin^4(3pi+theta)}-2{sin^6(pi/2+theta)+sin^6(5pi-theta)}`
View SolutionIf `t a n^2theta=1-a^2` , prove that `sectheta+t a n^3thetacos e ctheta=(2-a^2)^(3//2).`
View SolutionIf `acos^3theta+3acosthetasin^2theta=m and asin^3theta+3acos^2thetasintheta=n` , then prove that: `(m+n)^(2//3)+(m-n)^(2//3)=2a^(2//3)`
View SolutionIf `2t a n^2alphat a n^2betat a n^2gamma+t a n^2alphat a n^2beta+t a n^2betat a n^2gamma+t a n^2gammat a n^2alpha=1,` prove that `s i n^2alpha+s i n^2beta+s i n^2gamma=1` .
View SolutionIf `m^2 + m'^2 + 2mm' costheta = 1` and `n^2+n'^2+2n n'costheta=1`, `(mn + m' n' + (m n' + m' n) costheta = 0` prove that `m^2 + n^2 = cosec^2theta`
View SolutionIf `(sin^4theta)/a+(cos^4theta)/b=1/(a+b)` , prove that `(sin^8theta)/(a^3)+(cos^4theta)/(b^3)=1/((a+b)^3)` `(sin^(4n)theta)/(a^(2n-1))+(cos^(4n)theta)/(b^(2n-1))=1/((a+b)^(2n-1)),n in N`
View SolutionIf `(cos^4alpha)/(cos^2beta)+(sin^4alpha)/(sin^2beta)=1` prove that (i) `sin^4alpha+sin^4beta=2sin^2alphasin^2beta` (ii) `(cos^4beta)/(cos^2alpha)+(sin^4beta)/(sin^2alpha)=1`
View SolutionIf `x` is any non-zero real number, show that `costheta' a n d ' sintheta` can never equal to `x+1/x ,`
View SolutionIf `A=cos^2theta+sin^4theta,` prove that `3/4lt=Alt=1` for all values of `thetadot`
View SolutionIf `tantheta+sectheta=e^x` then `costheta` equals
View SolutionProve that:`sqrt((1+costheta)/(1-costheta))=cos e ctheta+cottheta` .
View SolutionProve the following identities: `sin^8theta-cos^8theta=(sin^2theta-cos^2theta)(1-2sin^2thetacos^2theta)`
View SolutionProve the following identities: `cot^4theta+cot^2theta=cos e c^4theta-"c o s e c"^2"theta"`
View SolutionProve the following identities: `2sec^2theta-sec^4theta-2cos e c^2theta+cosec^4 theta=cot^4theta-tan^4theta`
View SolutionProve the following identities: `(sintheta+cos e ctheta)^2+(costheta+sectheta)^2=7+tan^2theta+cot^2theta`
View SolutionProve the following identity: `(1+cottheta-cos e ctheta)(1+t a ntheta+s e ctheta)=2`
View SolutionProve the following identity: `(t a ntheta+s e ctheta-1)/(t a ntheta-s e ctheta+1)=(1+sintheta)/(costheta)`
View SolutionIf `costheta+sintheta=sqrt(2)costheta,` show that `costheta-sintheta=sqrt(2)sintheta`
View SolutionIf `acostheta+b sintheta=x` and ` asintheta-bcostheta=y` prove that `a^2+b^2=x^2+y^2`
View SolutionIf `tan theta +sin theta =m` and `tan theta -sin theta =n` then prove `m^2-n^2=4sqrt(mn)`
View SolutionProve the following identity: `sec^4theta-sec^2theta=tan^4theta+tan^2theta`
View SolutionProve that `sin^6theta+cos^6theta=1-3sin^2thetacos^2theta`
View SolutionProve the following identity: `(cosectheta-sintheta)(s e ctheta-costheta)(t a ntheta+cottheta)=1`
View SolutionProve the following identity: `cos e c\ theta(s e ctheta-1)-cottheta(1-costheta)=t a ntheta-sintheta`
View SolutionProve the following identity: `(1-sin AcosA)/(cos A(s e c A-cosec A))dot(sin^2A-cos^2A)/(sin^3 A+cos^3 A)=sin A`
View SolutionProve the following identity: `(t a n A)/(1-cot A)+(cot A)/(1-t a n A)=(s e c A\ cos e c\ A+1)`
View SolutionProve the following identity: `(sin^3A+cos^3A)/(sinA+cosA)+(sin^3A-cos^3A)/(sinA-cosA)=2`
View SolutionProve the following identity: `(s e c A\ s e c B+t a n AtanB)^2-(s e c A\ t a n B+t a n A s e c B)^2=1`
View SolutionProve the following identity: `(costheta)/(1-sintheta)=(1+costheta+sintheta)/(1+costheta-sintheta)`
View SolutionProve the following identity: `(tan^3theta)/(1+tan^2theta)+(cot^3theta)/(1+cot^2theta)=(1-2sin^2thetacos^2theta)/(sintheta\ costheta)`
View SolutionIf `(ax)/(costheta)+(by)/(sintheta)=a^2-b^2` , and `(axsintheta)/(cos^2theta)-(bycostheta)/(sin^2theta)=0`, prove that `(ax)^(2/3)+(by)^(2/3)=(a^2-b^2)^(2/3)`
View SolutionProve the following identity: `(1/(sec^2theta-cos^2theta)+1/(cos e c^2theta-sin^2theta))sin^2thetacos^2theta=(1-sin^2thetacos^2theta)/(2+sin^2thetacos^2theta)`
View SolutionProve the following identity: `(1+t a nalphat a nbeta)^2+(tanalpha-t a nbeta)^2=sec^2alphasec^2beta`
View SolutionProve the following identity: `((1+cottheta+t a ntheta)(sintheta-costheta))/(sec^3theta-cos e c^3theta)=sin^2thetacos^2theta`
View SolutionProve the following identity: `(2sinthetacostheta-costheta)/(1-sintheta+sin^2theta-cos^2theta)=cottheta`
View SolutionProve the following identity: `costheta(t a ntheta+2)(2t a ntheta+1)=2s e ctheta+5sintheta`
View SolutionIf `sintheta=(a^2-b^2)/(a^2+b^2),` find the value of `t a ntheta,\ s e ctheta\ a n d\ cos e ctheta`
View SolutionIf `t a ntheta=a/b ,\ ` show that `(a\ sintheta-b costheta)/(\ a\ sintheta+b\ costheta)=(a^2-b^2)/(a^2+b^2)`
View SolutionIf `cosectheta-sintheta=a^3, sectheta-costheta=b^3`, then prove that `a^2b^2(a^2+b^2)=1`
View SolutionIf `sintheta+costheta=m ,` then prove that `sin^6theta+cos^6theta=(4-3(m^2-1)^2)/4,\ w h e r e\ m^2lt=2.`
View SolutionFind the values of `cos theta` and `tan theta` when `sin theta =-3/5` and `pi < theta < (3pi)/2`
View SolutionIf `cos theta= -1/2` and `pi < theta < (3pi)/2` then find the value of `4tan^2 theta- 3cosec^2 theta`
View SolutionProve that: `sqrt((1-sintheta)/(1+sintheta))= sec theta- tan theta `when `(-pi/2) < theta < pi/2` and `-sec theta+tan theta` when `pi/2< theta< (3pi)/2`
View SolutionFind the values of the other five trigonometric functions I each of the following: `cottheta=(12)/5,theta` in quadrant III
View SolutionFind the values of the other five trigonometric functions in each of the following: `costheta=-1/2,theta` in quadrant II
View SolutionFind the values of the other five trigonometric functions in each of the following: `t a ntheta=3/4,theta` in quadrant III
View SolutionFind the values of the other five trigonometric functions in each of the following: `sintheta=3/5,theta` in quadrant I
View SolutionIf `sintheta=(12)/(13)a n d\ theta` lies in the second quadrant, find the values of `s e ctheta+t a nthetadot`
View SolutionIf `sintheta=3/5,tanphi=1/2 and pi/2ltthetaltpi phi<(3pi)/ 2`="" ,="" find="" the="" values="" of="" `8\="" t="" a="" ntheta-sqrt(5)\="" s="" e="" cvarphi`<="" b="">
View SolutionIf `costheta=-3/5 and pilttheta<(3pi)/2` find the values of other five trigonometric functions and hence evaluate`(cosectheta-cottheta)/(sectheta-tantheta)`.
View SolutionFind the values of the following trigonometric ratio: `sin315^0`
View SolutionFind the values of the following trigonometric ratio: `cos210^0`
View SolutionFind the values of the following trigonometric ratio: `"cos"(-480^0)`
View SolutionFind the values of the following trigonometric ratio: `sin(-1125^@)`
View SolutionProve that: `cos510^0cos 330^0+sin 390^0cos 120^0=-1.`
View SolutionProve that `("cos"(90^0+theta)"sec"(-theta)"tan"(180^0-theta))/("sec"(360^0-theta)"sin"(180^0+theta)"cot"(90^0-theta))=-1.`
View SolutionIf `A ,\ B ,\ C ,\ D` are angles of a cyclic quadrilateral, prove that `cos A+cos B+cos C+cos D=0.`
View Solution
All Questions questions and complete solutions for chapter TRIGONOMETRIC FUNCTIONS of RD SHARMA MATHS (ENGLISH) of Class 11