Complete Solutions to Exercise of chapter SIMPLE HARMONIC MOTION of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | SIMPLE HARMONIC MOTION |
| RESONANCE | Exercise |
| Number Of Questions | 28 |
| Academic Year | 2023-24 |
Equation of two S.H.M. `x_(1)=5 sin (2pi t+pi//4),x_(2)=5sqrt(2)(sin 2pit+cos 2pit)` ratio of amplitude & phase difference will be
A. `2:1,0`
B. `1:2,0`
C. `1:2,pi//2`
D. `2:1,pi//2`
View SolutionA particle is executing S.H.M. from mean position at 5 cm distance, acceleration is `20 cm//sec^(2)` then value of angular velocity will be
View SolutionA particle is executing a simple harmonic motion. Its maximum acceleration is `alpha` and maximum velocity is `beta`. Then, its time period of vibration will be
View SolutionA particle oscillating in simple harmonic motion has amplitude 'a'. The distance from the mean position at which its velocity will be one half of the maximum velocity is
View SolutionAcceleration versus time graph of a body in SHM is given by a curve shown below. T is the time period. Then corresponding graph between kinetic energy KE and time t is correctly represented by

View SolutionIn S.H.M., potential energy (U) V/s, time (t) . Graph is
View SolutionThe variation of the acceleration (f) of the particle executing S.H.M. with its displacement (X) is represented by the curve
View SolutionThe displecement-time graph of a particle execting SHM is shown in figure. Which of the following statements is false?
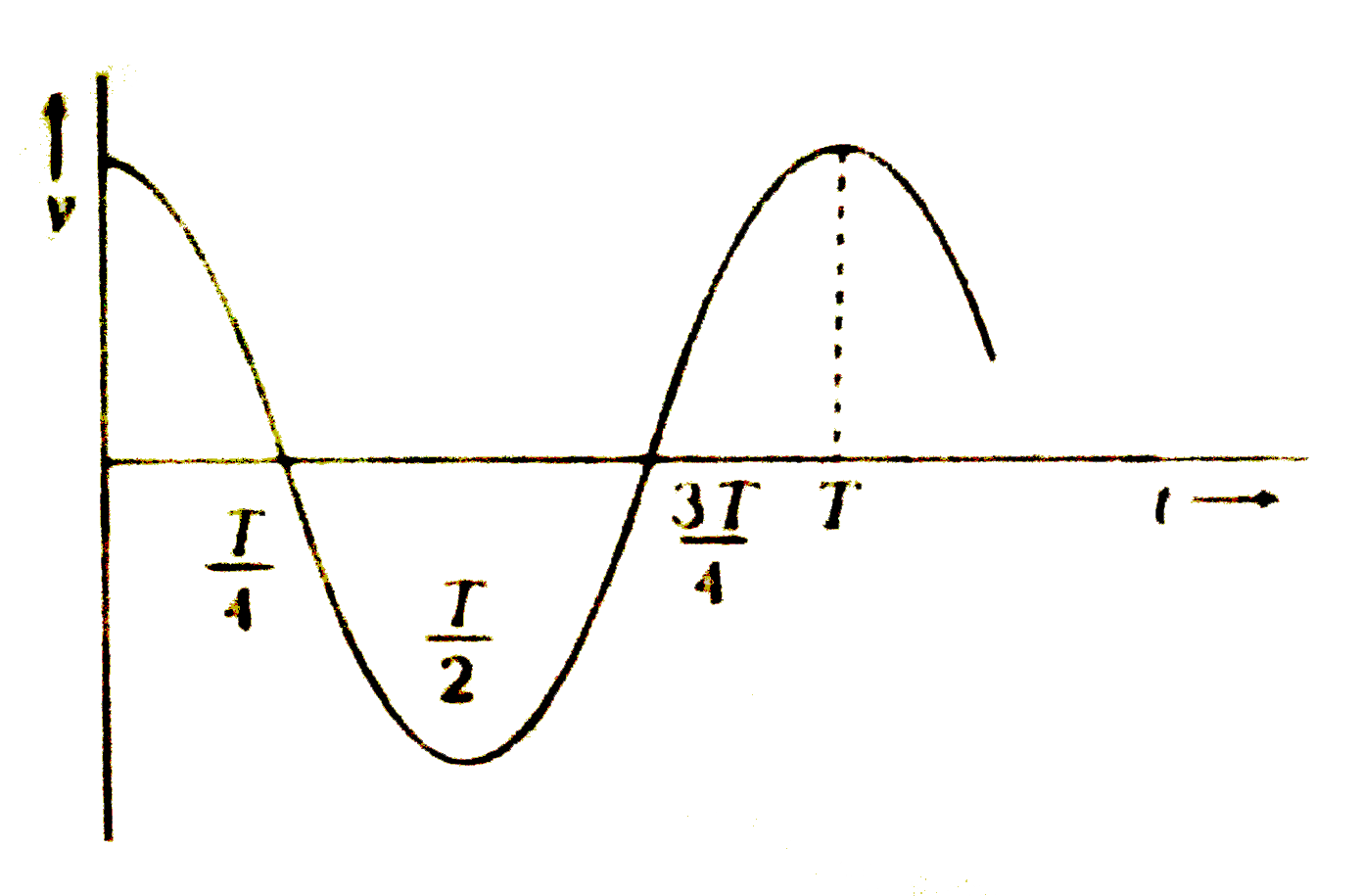
View SolutionFor a simple harmonic vibrator frequency n, the frequency of kinetic energy changing completely to potential energy is
View SolutionA particle is executing SHM with an amplitude 4 cm. the displacment at which its energy is half kinetic and half potential is
View SolutionFor a particle executing S.H.M. which of the following statements holds good `:`
View SolutionThe equation of SHM of a particle is `(d^2y)/(dt^2)+ky=0`, where k is a positive constant. The time period of motion is
View SolutionThe total energy of the body executing S.H.M. is E. Then the kinetic energy when the displacement is half of the amplitude is
View SolutionA linear harmonic oscillator of force constant `2 xx 10^(6)N//m` and amplitude `0.01 m` has a total mechanical energy of `160 J`. Its
View SolutionA particle executing SHM of amplitude 4 cm and T=4 s . The time taken by it to move from positive extreme position to half the amplitude is
View SolutionThe potential energy of a particle execuring S.H.M. is 5 J, when its displacement is half of amplitude. The total energy of the particle be
View SolutionA body of mass `m` is suspended from three springs as shown in figure. If mass `m` is displaced slightly then time period of oscillation is

View SolutionOne mass m is suspended from a spring. Time period of oscilation is T. now if spring is divided into n pieces & these are joined in parallel order then time period of oscillation if same mass is suspended.
View SolutionA spring has a certain mass suspended from it and its period for vertical oscillations is `T_(1)`. The spring is now cut into two equal halves and the same mass is suspended from one of the half. The period of vertical oscillation is now `T_(2)`. The ratio of `T_(2)//T_(1)` is
View SolutionTwo objects A and B of equal mass are suspended from two springs constants `k_(A)` and `k_(B)` if the objects oscillate vertically in such a manner that their maximum kinetic energies are equal, then the ratio of their amplitudes is
View SolutionIf the period of oscillation of mass M suspended from a spring is one second, then the period of 9M will be
View SolutionA simple pendulum suspended from the ceilling of a stationary trolley has a length l. its period of oscillation is `2pisqrt(l//g)`. What will be its period of oscillation if the trolley moves forward with an acceleration f ?
A. `2pisqrt(l/(f-g))`
B. `2pisqrt(l/(f+g))`
C. `2pisqrt(l/((f^(2)+g^(2))^(1//2)))`
D. `2pisqrt(l/(f^(2)-g^(2)))`
View SolutionIf length of simple pendulum is increased by 6% then percentage change in the time-period will be
View SolutionA man measures the period of a simple pendulum inside a stationary lift and finds it to be T sec. if the lift accelerates upwards with an acceleration g/6, then the period of the pendulum will be
View SolutionIn case of a forced vibration, the resonance wave becomes very sharp when the
View SolutionThe amplitude of a damped oscillator becomes half in one minutes. The amplitude after 3 minutes will be 1/x times of the original . Determine the value of x.
View SolutionStatement-1: kinetic energy of SHM at mean position is equal to potential energy at ends for a particle moving in SHM.
Statement-2: Total energy in SHM is conserved.
View SolutionStatement-1 : Frequency of kinetic energy of SHM is double that of frequency of SHM.
Statement-2. In SHM the velocity is ahead of displacement by a phase angle of `(pi)/2`.
View Solution
Exercise questions and complete solutions for chapter SIMPLE HARMONIC MOTION of RESONANCE ENGLISH of Class 11