Complete Solutions to Exercise of chapter STRING WAVES of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | STRING WAVES |
| RESONANCE | Exercise |
| Number Of Questions | 32 |
| Academic Year | 2023-24 |
two particle of medium disturbed by the wave propagation are at `x_(1)=0cm and x_(2)=1 cm`. The respective displacement (in cm) of the particles can be given by the equation:
`y_(1)=2 sin 3pi t, y_(2) sin (3pi t-pi//8)` the wave velocity is
View SolutionThe equation of a travelling wave is given as `y=5sin10pi(t-Q.01x),` along the x-axis . Here, all quantities are in SI units. The phase difference between the points separated by a distance of 10m alond x-axis is
View SolutionGraph show three waves that are separately send along a string that is stretched under a certain tension along `x-`axis. If `omega_(1).omega_(2)` and `omega_(3)` are their angular frequencies respectively then :
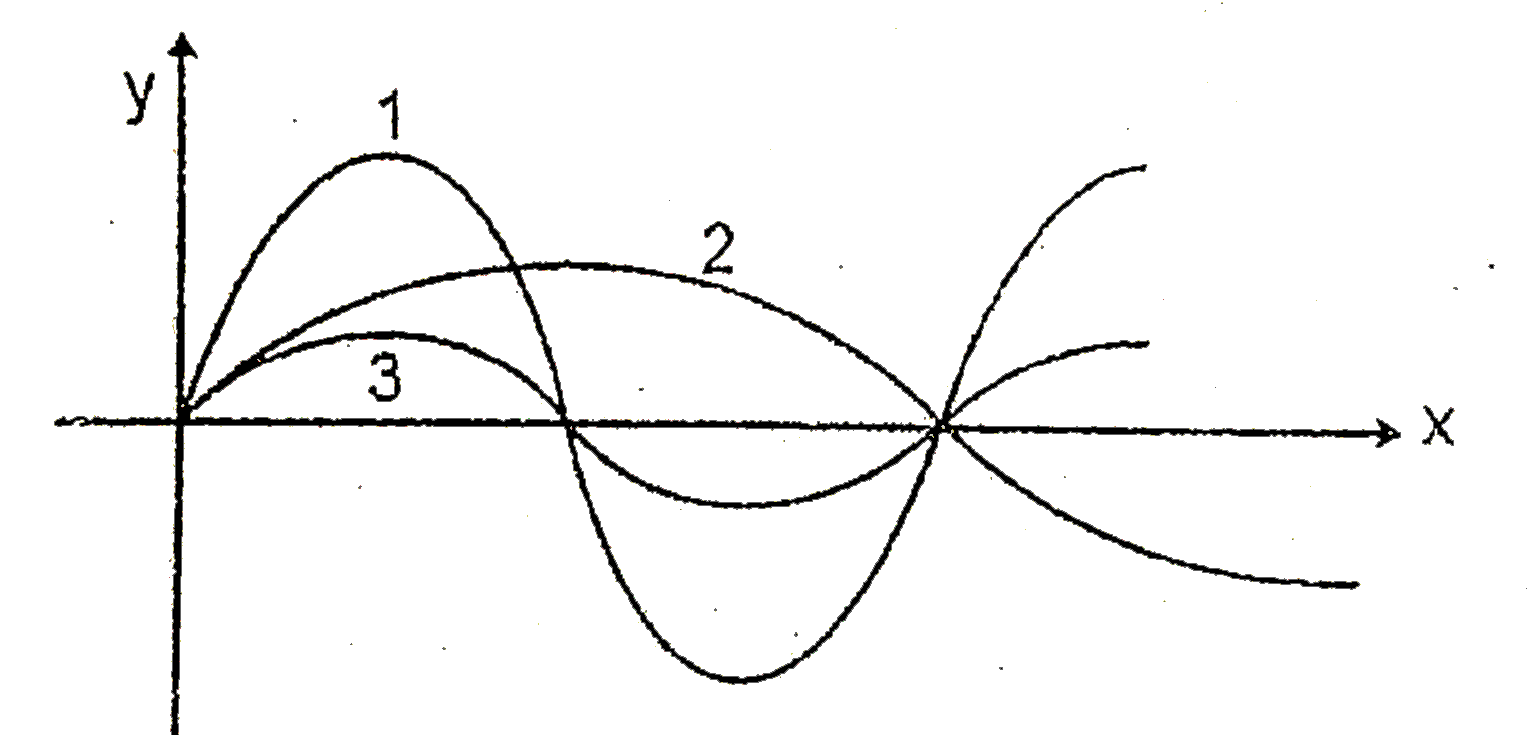
View Solutionthe same progressive wave is reprsented by two group I and II. Graoup I shows how the displacement 'y' varies with the distance x along the wave at a given time. Graph II shows how y varies with time t at a given point on the wave. The ratio of measurements AB to CD, marked on the curvse m repersents.
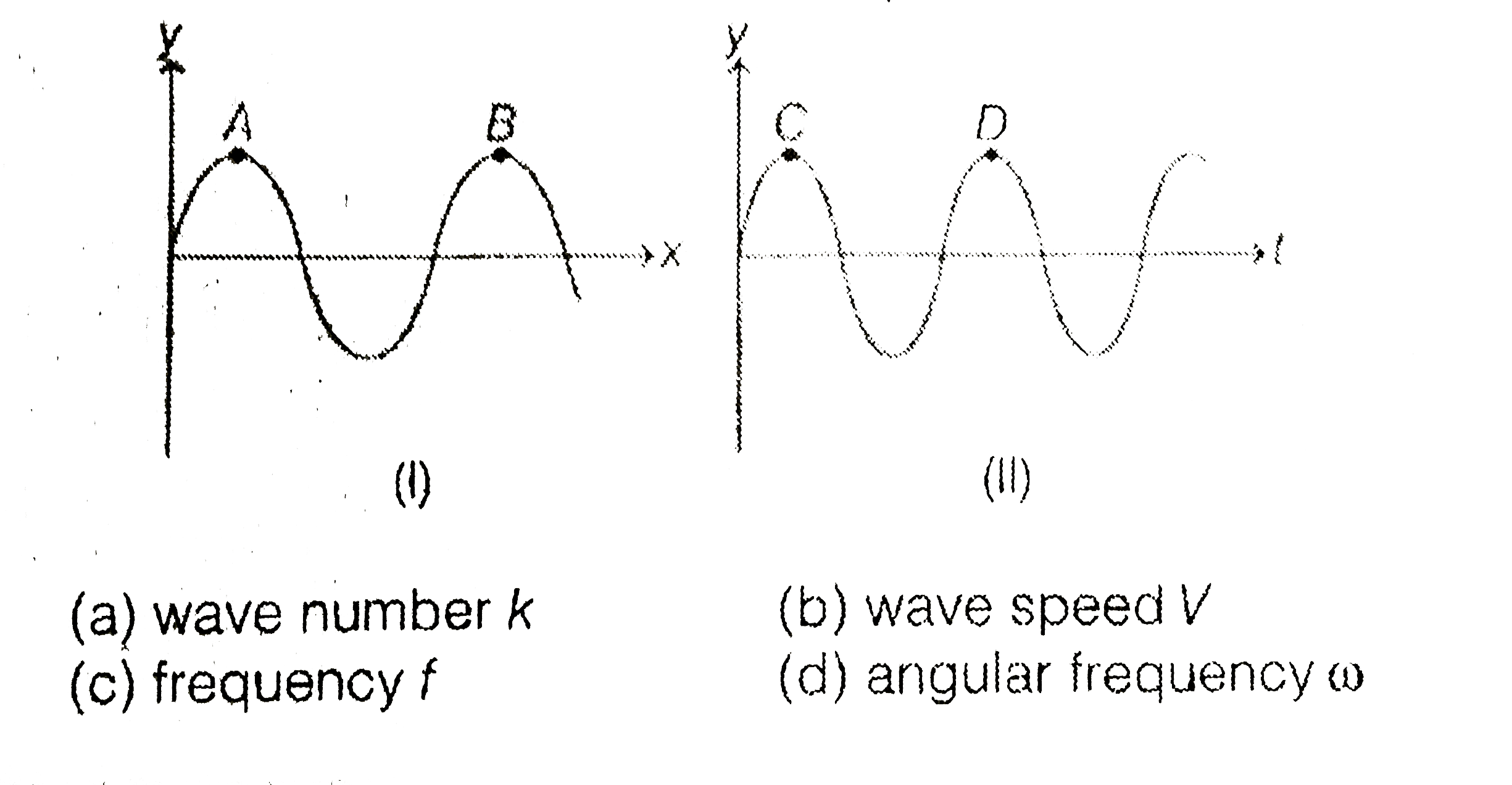
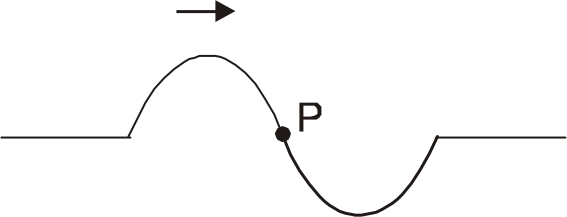
View SolutionA pulse on a string is shown in the figure.P is particle of the string.Then state which of the following are correct .
View SolutionA transverse wave described by equation `y=0.02sin(x+30t)` (where x and t are in meters and seconds, respectively) is travelling along a wire of area of cross-section `1mm^2` and density `8000kg//m^(2)`. What is the tension in the string?
View SolutionIf at `t = 0`, a travelling wave pulse in a string is described by the function,
`y = (10)/((x^(2) + 2 ))`
Hence, `x and y` are in meter and `t` in second. What will be the wave function representing the pulse at time `t`, if the pulse is propagating along positive x-axis with speed `2 m//s`?
View SolutionThe displacement from the position of equilibrium of a point 4 cm from a source of sinusoidal oscillations is half the amplitude at the moment `t=T//6` (T is the time perios). Assume that the source was at mean position at `t=0`. The wavelength of the running wave is :
A. 0.96 m
B. 0.48 m
C. 0.24 m
D. 0.12 m
View SolutionSinusoidal waves 5.00 cm in amplitude are to be transmitted along a string having a linear mass density equal to `4.00xx10^-2 kg//m`.If the source can deliver a average power of 90 W and the string is under a tension of 100 N, then the highest frequency at which the source can operate is (take `pi^2=10`):
View SolutionTwo interferring waves have the same wavelength, frequency and amplitude. They are travelling in the same direction but `90^(@)` out of phase compared to individual waves. The resultant wave will have the same.
View SolutionA travelling wave `y=A sin (kx- omega t +theta )` passes from a heavier string to a lighter string. The reflected wave has amplitude `0.5A` . The junction of the strings is at `x=0`. The equation fo the refelcted wave is `:`
View SolutionThe figure shows three progressive waves A, B and c. wahat canbe concluded from the figure that with respect to wave A?
View SolutionTwo wave function in a medium along x direction are given by
`y_(1)=1/(2+(2x-3t)^(2))m`, `y_(2)=-1/(2+(2x+3t-6)^(2))m`
Where x is in meters and t is in seconds
A. There is no position at which resultant displacement will be zero at all times
B. There is no time at which resultant displacement will be zero everywhere.
C. Both waves travel in same directions.
D. Both waves travel in oppoisite directions.
View SolutionWhen a wave pulse travelling in a string is reflected from a rigid wall to which string is tied as shown in figure. For this sitution two statements are given below.
(1) The reflected pulse in same orientation of incident pulse due to a phase change of `pi` radians
(2) During relfection the wall exerts a force on string in upward direction

View SolutionA wire of length 'l' having tension T and radius 'r' vibrates with fundamental frequency 'f'.Another wire of the same metal with length 2l having tension 2 T and radius 2 r will vibrate with fundamental frequency:
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode Amplitude at the centre of the string is 4 mm. Distance between the two points having amplitude 2mm is
View SolutionWhat is the percentage change in the tension necessary in a sonometer of fixed length to produce a note one octave lower (half of original frequency) than before?
View SolutionA string of length 'l' is fixed at both ends. It is vibrating in tis 3rd overtone with maximum amplitude 'a' the amplitude at a distance `l/3` from one end is
View SolutionTwo vibrating strings of same material stretched under same tension and vibrating with same frequency in the same overtone have radii 2r and r. Then the ratio of their lengths is:
View SolutionWhich of the following travelling wave will produce standing wave , with nodes at `x = 0`, when superimosed on ` y = A sin ( omega t - kx)`
View SolutionA standing wave pattern is formed on a string One of the waves if given by equation `y_1=acos(omegat-kx+(pi)/(3))` then the equation of the other wave such that at `x=0` a node is formed.
View Solution`S_(1)` : A standing wave pattern if formed in a string. The power transfer through a point (other than node and antinode) is zero always
`S_(2)`: if the equation of transverse wave is `y= sin 2pi[t/0.04-x/40]`, where distance is in cm. time in second, then the wavelength will be 40 cm.
`S_(3)`: if the length of the vibrating string is kept constant, then frequency of the string will be directly proportional to `sqrt(T)`
View Solution`S_(1)`: The particles speed can never be equal to the wave speed in sine wave if the amplitude is less then wavelength divided by `2pi`.
`S_(2)`: In transverse wave of amplitude A, the maximum particle velocity is four times its wave velocity. Then, the wave length of the wave is `piA`
`S_(3)`: the phase difference between two points separated by 1m in a wave of frequency 120 Hz is `90^(@)`. the velocity of the wave is 480 m/s
View SolutionTwo small boat are `10 m` apart on a lake. Each pops up and down with a period of `4.0` seconds due to wave motion on the surface of water. When one boat is at its highest point, the other boat is at its lowest point. Both boats are always within a single cycle of the waves. The speed of the waves is :
View SolutionThree waves of equal frequency having amplitudes `10mum`, `4mum`, `7mum` arrive at a given point with successive phase difference of `pi//2`, the amplitude of the resulting wave in `mum` is given by
View SolutionWhat is the second lowest frequency for standing waves on a wire that is 10.0 m long has a mass of 100 g and is stretched under a tension of 25 N which is fixed at both ends ?
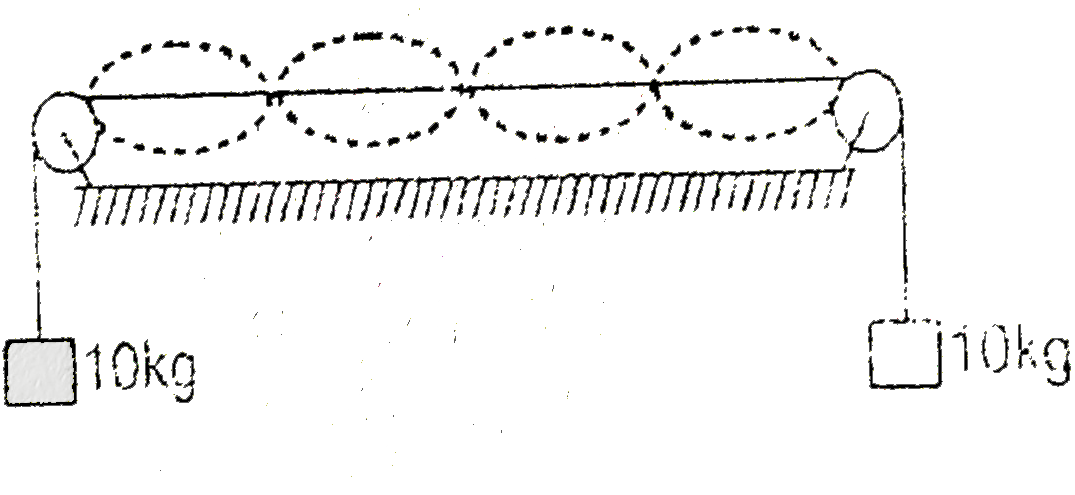
View SolutionThe length of a shown in figure betweenn the pulleys is `1.5 m` and its mass is `15 g`. Find the freqency of vibration with which the wire vibrates in four loops leaving the middle point of the wire between the pulleys at rest. `(g = 10 m//s^(2))`
View SolutionThe equation of a wave traveling on a string is `y=4sin.(pi)/(2)(8t-(x)/(8))`. If x and y are in cm, then velocity of wave is
View SolutionThe equation of a progressive wave is given by `y=a sin (628t-31.4x)`. If the distance are expressed in cms and time seconds, then the wave in this string wll be
View SolutionA string is stretched by a force of 40 newton. The mass of 10 m length of this string is 0.01 kg. the speed of transverse waves in this string will be
View SolutionThe density of the material of a wire used in sonometer is `75xx10^(-2) kg //m^(3)`. If the stress on the wire is `3.0xx10^(4) N//m^(2)`, the speed of transverse wave in the wire will be
View SolutionAssertion: In a small segment of string carrying sinusoidal wave, total energy is conserved.
Reason: Every small part moves in SHM and total energy of SHM is conserved.
View Solution
Exercise questions and complete solutions for chapter STRING WAVES of RESONANCE ENGLISH of Class 11