Complete Solutions to Exercise of chapter WAVE OPTICS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | WAVE OPTICS |
| RESONANCE | Exercise |
| Number Of Questions | 35 |
| Academic Year | 2023-24 |
If the relative permitivity and relative permeability of a medium are 2 and 1.28 respectively, then refractive index of that material is:
View SolutionTwo light waves travelling in same medium are given by `E_(1)=2sin(100pit-kx+30^(@))` and `E_(2)=3cos(200pit-k^(')x+60^(@))`. The ratio of intensity of first wave to that of second wave is:
View SolutionIf the ratio of the intensity of two coherent sources is 4 then the visibility `[(I_(max)-I_(min))//(I_(max)+I_(min))]` of the fringes is
View SolutionThe distance of `n^(th)` bright fringe to the `(n+1)^(th)` dark fringe in Young's experiment is equal to:
View SolutionIn Young's double slit experiment, we get `60` fringes in the field of view of monochromatic light of wavelength `4000Å`. If we use monochromatic light of wavelength `6000Å`, then the number of fringes obtained in the same field of view is
View SolutionIf the distance between the first maxima and fifth minima of a double-slit pattern is 7 mm and the slits are separated by 0.15 mm with the screen 50 cm from the slits, then wavelength of the light used is
View SolutionIn Young'double-slit interference experiment, if the slit separation is made threefold, the fringe width becomes
View SolutionThe path difference between two interfering waves at a point on the screen is `lambda // 6`, The ratio of intensity at this point and that at the central bright fringe will be (assume that intensity due to each slit is same)
View SolutionIf the first minima in Young's double-slit experiment occurs directly in front of one of the slits (distance between slit and screen `D = 12 cm` and distance between slits `d = 5 cm)`, then the wavelength of the radiation used can be
View SolutionTwo coherent ligh sources each of wavelength `lambda` are separated by a distance `3lambda`. The maximum number of minimas formed on line AB which runs from `-oo " to " +oo` is
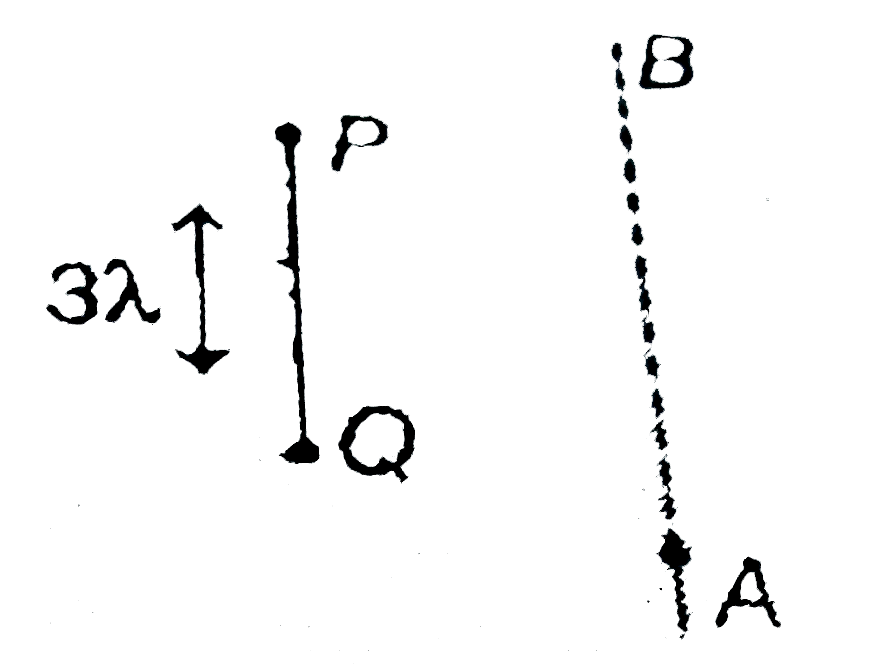
View SolutionA thin oil film of refracting index `1.2` floats on the surface of water `(mu=4/3)`. When a light of wavelength `lamda=9.6xx10^(-7)m` falls normally on the film air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is `Zxx10^(-7)m`. Then find `Z`.
View SolutionThe wavefront of a light beam is given by the equation `x + 2y + 3x = c` (where c is arbitrary constant), then the angle made by the direction of light with the y-axis is
View SolutionIn a single-slit diffraction experiment, the width of the slit is made half of the original width:
View SolutionOn a very hot day, a boy standing at a large distance observers a neon monochromatic lamp hanging at a height h above the ground. He observe the lamp as shown in the figure
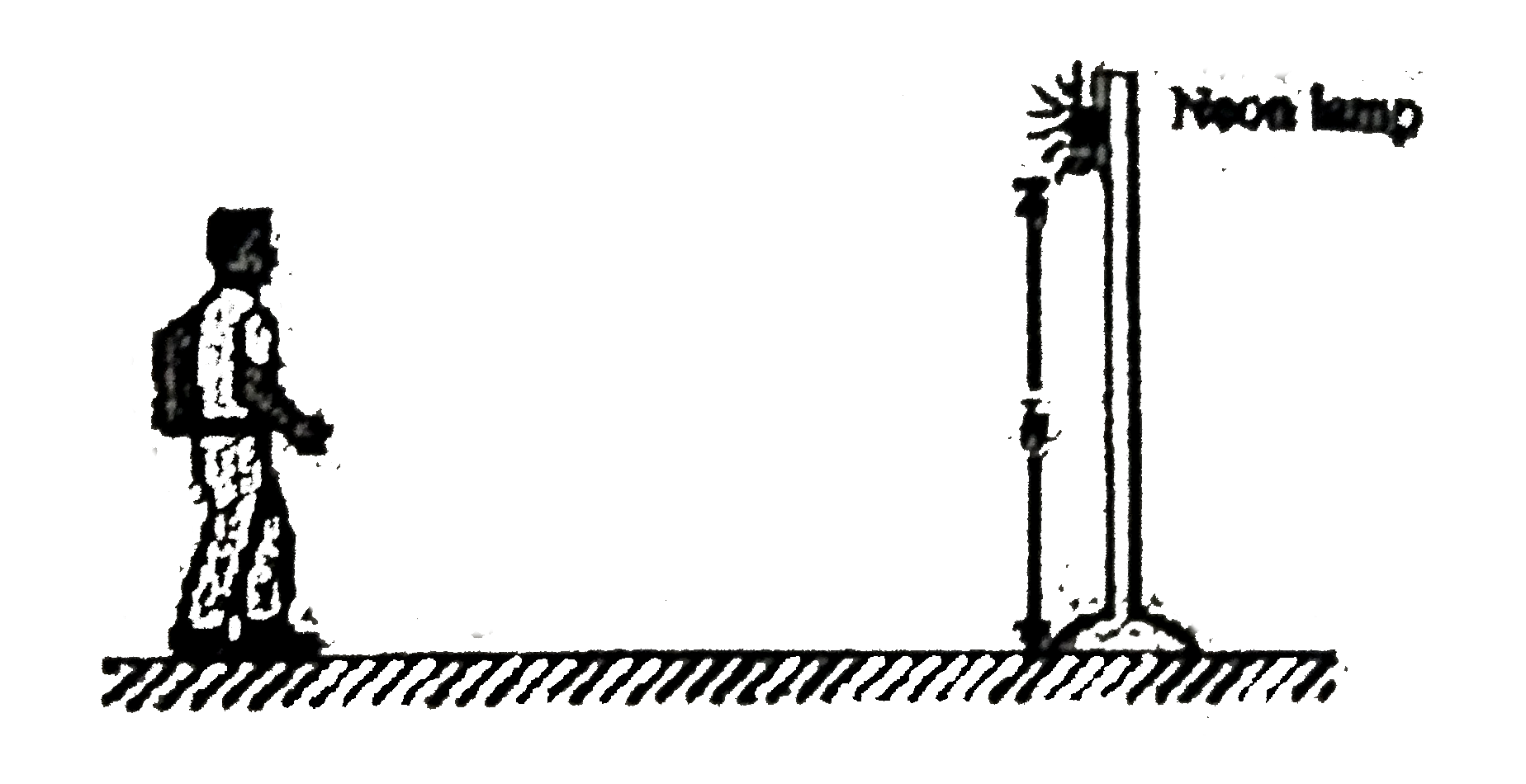
View SolutionIf torch is used in place of monochromatic light in Young's experiment what will happen
View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance `d (gt gtb)` from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View SolutionThe ratio of intensities of two waves are given by `4:1`. The ratio of the amplitudes of the two waves is
View SolutionTwo coherent monochromatic light beams of intensities I and 4I are superposed. The maximum and minimum possible intensities in the resulting beam are
View SolutionThe contrast in the fringes in any interference pattern depends on -
View SolutionYoung's experiment is performed in air and then performed in water, the fringe width:
View SolutionThe Youn'g double slit experiment is performed with blue and green light of wavelength `4360Å` and `5460Å` respectively, if x is the distance of 4th maxima from the central one, then
View SolutionA light ray incidents on water `(n=4/3)` surface from air and reflected from air and reflected part of it is found to be polarized. Find the deviation of refracted light from its original path:
View SolutionIn a Fresnel biprism experiment the two positions of lens give separation between the slits as 16 cm and 9 cm respectively. The actual distance of separation is
View SolutionThe ratio of diameters of fourth and ninth half period zones is:
View SolutionThe maximum numbers of possible interference maxima for slit separation equal to twice the wavelength in Young's double slit experiment is
View SolutionCalculate the width of central maxima, if light of 9000Å incidents upon a slit of width 1.5 mm. Screen is kept 150 cm away from the slit.
View SolutionTwo slits at a distance of `1mm` are illuminated by a light of wavelength `6.5xx10^-7m`. The interference fringes are observed on a screen placed at a distance of `1m`. The distance between third dark fringe and fifth bright fringe will be
View SolutionA parallel beam of monochromatic light is used in a Young's double slit experiment. The slits are separated by a distance d and the screen is placed parallel to the plane of the slits. Show that if the incident beam makes an angle `theta=sin^-1(lamda/(2d))` with the normal to the plane of the slits, there will be a dark fringe at the centre Po of the pattern.
View SolutionWhich of the following statement is correct?
View SolutionA single slit of width 0.1mm is illuminated by parallel light of wavelength 6000Å, and diffraction bands are observed on a screen 40cm from the slit. The distance of third dark band from the central bright band is:
View SolutionA light wave of frequency `5 xx 10^(14)` Hz enters a medium of refractive index 1.5. In the medium, the velocity of the ligth of wave is `"________"` and its wavelength `"_________"`,
View SolutionIf one of the slit of a standard Young's double slit experiment is covered by a thin parallel sided glass slab so that it transmits only one-half the light intensity of the other, then
View SolutionA Young's double slit experiment is performed with white light.
View SolutionA parallel beam of light `(lambda= 5000 Å)` is incident at an angle `theta=30^@` with the normal to the slit plane in a Young's double slit experiment. The intensity due to each slit is `I_0`. Point O is equidistant from `S_1 and S_2`. The distance between slits is 1mm.
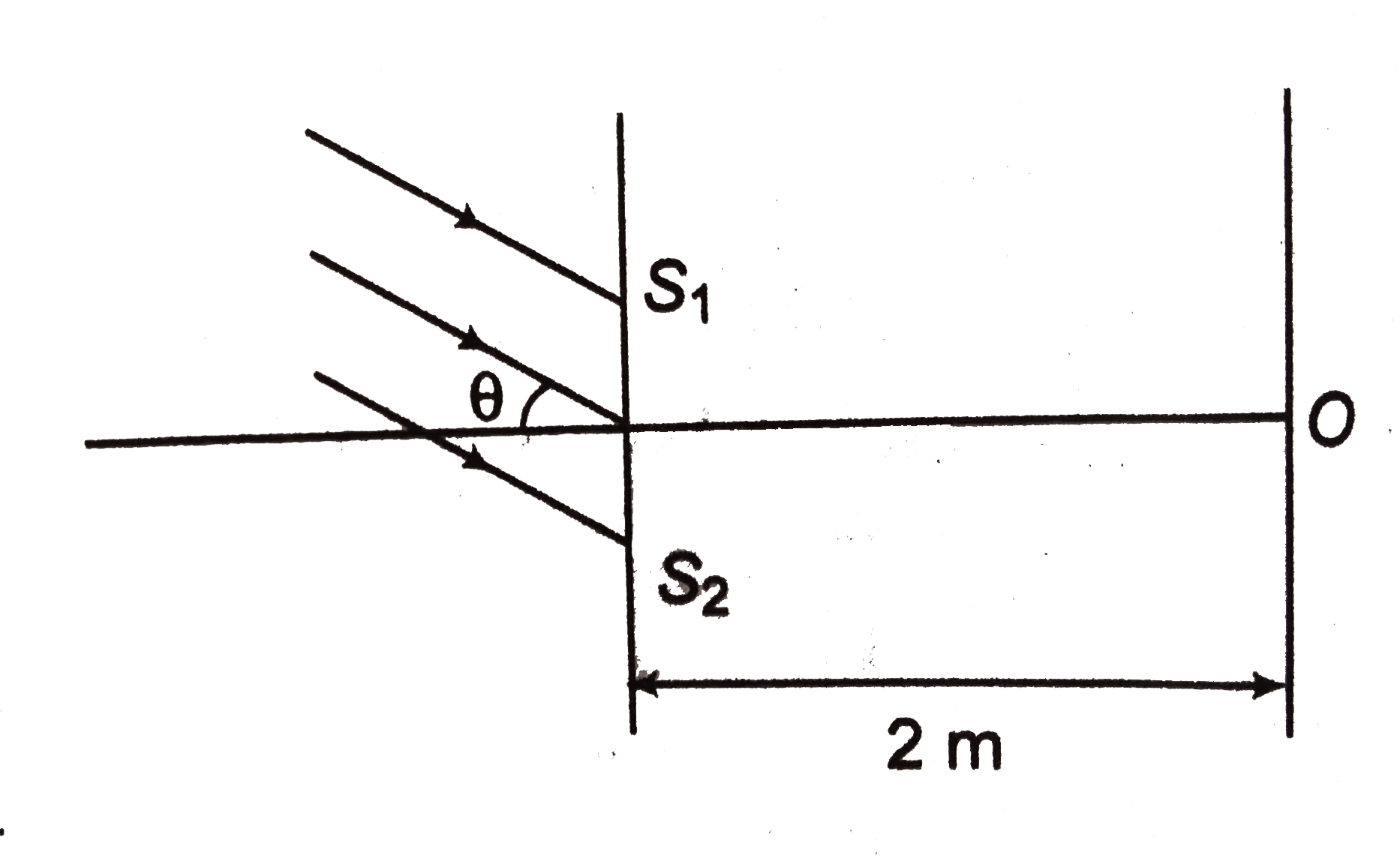
View SolutionStatement I: Two coherent point sources of light having no-zero phase difference are separated by a small distance. Then, on the perpendicular bisector of line segment joining both the point sources, constructive interference cannot be obtained.
Statement II: For two waves from coherent point sources to interfere constructively at a point, the magnitude of their phase difference at that point must be `2 m pi` (where m is non-negative integer).
View Solution
Exercise questions and complete solutions for chapter WAVE OPTICS of RESONANCE ENGLISH of Class 11