Complete Solutions to गत वर्षो के विभिन्न प्रतियोगी परीक्षाओ में पूछे प्रश्न of chapter कार्य ऊर्जा और शक्ति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | कार्य ऊर्जा और शक्ति |
| SANJEEV PUBLICATION | गत वर्षो के विभिन्न प्रतियोगी परीक्षाओ में पूछे प्रश्न |
| Number Of Questions | 23 |
| Academic Year | 2023-24 |
किसी कण पर `( 4 hat(i) + 3hat(j)) N ` बल लगाने पर वह बिंदु `(-2 hat(i) + 5 hat(j))` से बिंदु `( 4 hat(j) + 3hat(k))` तक विस्थापित हो जाता है । इस प्रक्रिया में बल द्वारा किया गया कार्य -
View Solutionजब एक रबड़ के छल्ले को x दूरी तक तानित किया जाता है , तब परिमाण `F = ax+bx^(2)` एक प्रत्यन्न बल लगता है , वहाँ a तथा b स्थिरांक है बिना तनित रबड़ के छल्ले की L से तानित करने में किया गया कार्य है -
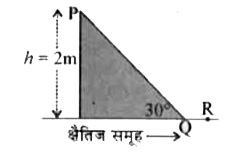
View Solutionm द्रव्यमान का एक बिंदु कण एक बिंदु एक खुरदरे पथ PQR ( चित्र देखिये ) पर चल रहा है। कण और पथ के बीच घर्षण गुणांक `mu` है। कण , P से छोड़े के बाद R पर पहुँच कर रूक जाता है । पथ के भाग PQ और QR पर चलने में कण द्वारा खर्च की गई उर्जाएँ बराबर है । PQ से QR पर होने वाले दिशा बदलाव में कोई खर्च नहीं होती । तब `mu` और दूरी `x ( = QR)`के मान लगभग है क्रमशः -
View Solutionकिसी बल क्षेत्र में कण की स्थितिज ऊर्जा निम्नलिखित है -
`U = A/(r^(2)) - B/r`
जहाँ A तथा B धनात्मक नियतांक है तथा r कण की बल क्षेत्र के केंद्र से दूरी है स्थायी संतुलन की दशा में कण की दूरी होगी -
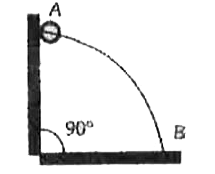
View Solutionएक तार जो एक छोटे मोती के मध्य में स्थित छिद्र से गुजरता है , को एक चतुर्थाश वृत्त के अनुरूप मोड़ा गया है तार को भूमि पर ऊर्ध्वातल में स्थित किया गया है जैसा चित्र में दर्शाया गया है । मोती को तार के ऊपरी सिरे से छोड़ा जाता है , जिससे यह तार के अनुदिश बिना किसी घर्षण से सरकता है। जब मोती A से B तक सरकता है , तब इसके द्वारा तार पर लगने वाला बल है -
View Solution` 400 ms^(-1)` के क्षैतिज वेग से चलती हुई 10 g द्रव्यमान की एक गोली 2 kg द्रव्यमान के लकड़ी के एक गुटके से टकराती है। यह गुटका एक 5 m लम्बी हल्की अवितान्य डोरी से लटका है। यदि गोली के टकराने के परिणामस्वरूप गुटके का गुरुत्व केंद्र 10 cm ऊर्ध्वाधर ऊपर उठ जाता है , तो गुटके से क्षैतिज दिशा में बाहर निकलने पर गोली की चाल होगी -
View Solutionएक कण किसी एक आकर्षण विभव `U = k/(2r^(2))` के अंतर्गत त्रिज्या a के एक गोलाकार पथ में चल रहा है , उसकी ऊर्जा होगी -
View Solution1 kg द्रव्यमान का कोई पिंड किसी कालाश्रित बल , ` bar(F) = (2 hat(ti) + 3t^(2)hat (j))N,` यहाँ `hat(i)` और `hat(j)` x-तथा y-अक्ष के इकाई वेक्टर हैं, समय t पर इस बल द्वारा विकसित शक्ति क्या होगी -
View Solutionx - दिशा में 2v चाल से चलते हुए द्रव्यमान के एक कण से , y - दिशा में v वेग से चलता हुआ 2m द्रव्यमान का एक कण टकराता है यदि यह संघट्ट ( टक्कर ) पूणतः अप्रत्यास्थ है तो टक्कर के दौरान ऊर्जा का क्षय ( हानि ) होना -
View Solutionकिसी घर्षणहीन पृष्ठ पर v चाल से चलता हुआ M द्रव्यमान का एक ब्लॉक उसी द्रव्यमान M के विरामावस्था में स्थित एक अन्य ब्लॉक से टकराता है। टक्कर के पश्चात पहला ब्लॉक चाल `v/3` से अपनी प्रारंभिक गति की दिशा से `theta ` कोण पर चलने लगता है तो टक्कर के पश्चात दूसरे ब्लॉक की चाल होगी।
View Solutionदो एकसमान गेंदों A तथा B के वेग क्रमशः `0.5 m//s` तथा `-0.3 m//s` है। ye एक रेखा के अनुदिश चलते हुए टकराती है। यदि यह टक्कर प्रत्यास्थ है , इस टक्कर के पश्चात A तथा B के वेग क्रमशः होंगे -
View Solutionएक द्रव्यमान m एवं प्रारंभिक वेग v के एक कण A की टक्कर द्रव्यमान `m/2` के स्थिर कण B से होती है। यह टक्कर सम्मुख एवं प्रत्यावस्था है। टक्कर के बाद डी - ब्रोग्ली तरंगदैर्घ्य `lambda_(A)` से `lambda_(B)`का अनुपात होगा -
View Solutionद्रव्यमान m का एक गतिशील गुटका 4 m द्रव्यमान के किसी दूसरे स्थिर गुटके से संघट्ट करता है । संघट्ट के पश्चात हल्का गुटका विराम अवस्था में आ जाता है । यदि हलके गुटके का आरंभिक वेग है तो प्रत्यानयन गुणांक का मान होगा -
View Solution1 Kg द्रव्यमान का एक कण समय पर निर्भर F= 6t बल का अनुभव करता है यदि कण विरामावस्था से चलता है तो पहले 1 सेकंड में बल द्वारा किया गया कार्य होगा -
View Solutionद्रव्यमान `m= 10^(-2)`किलोग्राम का एक पिंड एक माध्यम से गति कर रहा है और एक घर्षण बल `F=-kv^(2)` का अनुभव करता है पिण्ड का प्रारंभिक वेग `v_(0)= 10 ms^(-1)` है यदि 10 सेकंड के बाद उसकी ऊर्जा `1/8mv_(0)^(2)` है तो `k` का मान होगा -
View Solutionद्रव्यमान 'm' का एक कण चाल '2v' से जाते हुए एक द्रव्यमान '2m' के कण जो इसी दिशा में चाल 'v' से जा रहा है , से संघट्ट करता है । संघट्ट के बाद पहला कण स्थिर अवस्था में आ जाता है तथा दूसरा कण ही द्रव्यमान 'm' के दो कणो में विभाजित हो जाता है । ये दोनों कण आरंभिक दिशा से `45^(@)` के कोण पर जाते है । ये दोनों कण आरंभिक दिशा से के कोण पर जाते है । प्रत्येक चलायमान कण की गति का मान होगा -
View Solution`M= 4m` द्रव्यमान का एक वेज आकार का गुटका एक घर्षणहीन सतह पर रखा है । m द्रव्यमान का एक कण गुटके की ओर v वेग से आता है । कण और सतह या कण और गुटके की और कोई घर्षण नहीं है। कण के द्वारा गुटके के ऊपर छड़ी गयी अधिकतम ऊँचाई होगी।
View Solutionएक टेनिस की गेंद को एक क्षैतिज चिकनी सतह पर गिराया जाता है । गेंद सतह से टकराने के पश्चात पुनः अपने मूल स्थान पर पहुँच जाती है । संघट्ट के दौरान , गेंद पर लगने वाला बल उसकी संपीडन लम्बाई के अनुक्रमानुपाती है। निम्न में से कोण सा रेखाचित्र , समय t के सतह गेंद की गतिज ऊर्जा K के परिवर्तन को सर्वाधिक उचित रूप से प्रदर्शित करता है । ( चित्र केवल सांकेतिक है और मापन के अनुरूप नहीं है - )
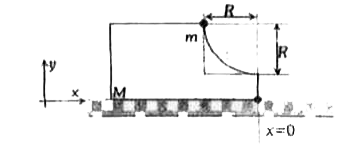
View Solutionवृत्ताकार चाप वाले एक गुटके का द्रव्यमान M है। ये गुटका एक घर्षण रहित एक मेज पर स्थित है । मेज के सापेक्ष गुटके का दाहिना कोर x=0 पर स्थित है। द्रव्यमान m वाले एक बिंदु कण को वृत्ताकार चाप के उच्चतम बिंदु से विरामावस्था से छोड़ा जाता है । ये बिंदु कण वृत्ताकार पथ पर निचे की और सरकता है । जब बिंदु कण गुटके से संपर्क विहीन हो जाता है , तब उसकी तात्क्षणिक स्थिति x और गति v है। निम्न में से कौन सा ( से ) कथन सही है / हैं -
View Solution1 Kg द्रव्यमान के एक कण एक स्थिर 5 द्रव्यमान के कण से प्रत्यास्तथा टकराता है टकराने के बाद 1 kg का कण `2 ms^(-t)` चाल से पहले की विपरीत दिशा में जाने लगता है । इन दो द्रव्यमानो के बारे में निम्न में से कौन सा प्रकथन सही है -
View Solutionm द्रव्यमान का एक छोटा गुटका नत - समतल की घर्षण रहित सतह पर गति करता है ( चित्रानुसार )। नत - समतल का झुकाव कोण अचानक बिंदु B पर `60^(@)` से `30^(@)` परिवर्तित हो जाता है । प्रारम्भ में गुटका ,A पर विराम में है । मान लीजिये की गुटके व नत - समतल के मध्य संघट्ट पूर्णतः अप्रत्यास्थ है । (`g = 10 m//s^(2)`)
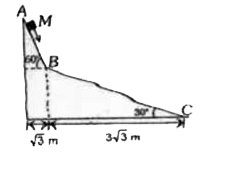
द्वितीय नत तल पर टकराने के तुरंत बाद गुटके की बिंदु B पर चाल है -
View Solutionm द्रव्यमान का एक छोटा गुटका नत - समतल की घर्षण रहित सतह पर गति करता है ( चित्रानुसार )। नत - समतल का झुकाव कोण अचानक बिंदु B पर `60^(@)` से `30^(@)` परिवर्तित हो जाता है । प्रारम्भ में गुटका ,A पर विराम में है । मान लीजिये की गुटके व नत - समतल के मध्य संघट्ट पूर्णतः अप्रत्यास्थ है । (`g = 10 m//s^(2)`)
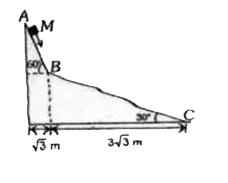
द्वितीय नत - तल को छोड़ने के तुरंत पूर्व बिंदु C पर गुटके की चाल है -
View Solutionm द्रव्यमान का एक छोटा गुटका नत - समतल की घर्षण रहित सतह पर गति करता है ( चित्रानुसार )। नत - समतल का झुकाव कोण अचानक बिंदु B पर `60^(@)` से `30^(@)` परिवर्तित हो जाता है । प्रारम्भ में गुटका ,A पर विराम में है । मान लीजिये की गुटके व नत - समतल के मध्य संघट्ट पूर्णतः अप्रत्यास्थ है । (`g = 10 m//s^(2)`)
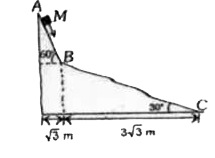
यदि गुटके व नत - तल के मध्य संघट्ट पूर्णतः प्रत्यास्थ हो , तब द्वितीय नट - तल टकराने के तुरंत पश्चात बिंदु B पर गुटके क वेग का ऊर्ध्वाधर ( ऊपर की दिशा में ) घटक होगा -
View Solution
गत वर्षो के विभिन्न प्रतियोगी परीक्षाओ में पूछे प्रश्न questions and complete solutions for chapter कार्य ऊर्जा और शक्ति of SANJEEV PUBLICATION of Class 11
All Exercises from SANJEEV PUBLICATION Class 11 PHYSICS कार्य ऊर्जा और शक्ति
- अन्य महत्वपूर्ण कीजिये ( कॉलम से कॉलम का सही मिलान कीजिये )
- अन्य महत्वपूर्ण प्रश्न ( नीचे दिए गए वाक्यों में सत्य /असत्य कथन का चयन कीजिये - )
- अन्य महत्वपूर्ण प्रश्न ( बहुचयनात्मक प्रश्न )
- अन्य महत्वपूर्ण प्रश्न ( रिक्त स्थानों के प्रश्न )
- अन्य महत्वपूर्ण प्रश्न (अतिलघुरात्मक प्रश्न )
- अन्य महत्वपूर्ण प्रश्न (आंकिक प्रश्न )
- अन्य महत्वपूर्ण प्रश्न (निबंधनात्मक प्रश्न )
- अन्य महत्वपूर्ण प्रश्न (लघुरात्मक प्रश्न )
- अभ्यास के अतिरिक्त प्रश्न -
- उदाहरण
- गत वर्षो के विभिन्न प्रतियोगी परीक्षाओ में पूछे प्रश्न
- पाठ्य पुस्तक के प्रश्न