Complete Solutions to गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न of chapter कणों के निकाय तथा घूर्णी गति of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | कणों के निकाय तथा घूर्णी गति |
| SANJEEV PUBLICATION | गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
किसी एकसमान ठोस शंकु के द्रव्यमान केंद्र की उसके शीर्ष से दूरी `z_(0)` हैं । यदि शंकु के आधार की त्रिज्या R तथा शंकु की ऊंचाई h हो तो `z_(0)` का मान निम्नांकित में से kiske बराबर होगा -
View Solutionविभिन्न द्रव्यमानों के तीन पिंड x- अक्ष पर इस प्रकार रखते हैं की 300 g का पिंड मूल बिंदु पर 500 g का x = 40 cm पर तथा 400 g का x = 70 cm पर हो तो मूलबिंदु से द्रव्यमान केंद्र की दूरी होगी -
View Solutionचित्र द्वारा दर्शाये संबहुभुजाओं की संख्या n = 3,3,5 ..... है । सभी बहुभुजाओं का संहित केंद्र अनुभूमिक तल से h ऊंचाई पर है । बिना फिसले क्षैतिज तल पर प्रतिगामी शीर्ष के चारों ओर घूर्णन कर अर्गसृत हो रहे हैं । प्रत्येक बहुभुज के संहित केंद्र के रेखापाठ की ऊंचाई की अधिकतम वृद्धि `Delta` है । तब `Delta` की h और n पर निर्भरता निम्न में से दी जायगी -
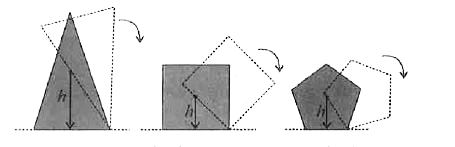
View Solutionएक हल्की छड़ की लम्बाई l है । इसके दो सिरों से क्रमश :` m_(1)` तथा `m_(2)` द्रव्यमान के पिंड संग्लन हैं । इस छड़ के लंबवत तथा इसके द्रव्यमान केंद्र से गुजरते हुए अक्ष के परित इस निकाय का जड़त्व आघूर्ण होगा -
View Solutionएक त्रिज्या R तथा लम्बाई l के एक समान बेलन का उसके अभिलम्ब द्विभाजक के सापेक्ष जड़त्व अपूर्ण I है । जड़त्व आपूर के निम्नतम मान के लिए अनुपात I/R क्या होगा -
View Solutionचित्रानुसार सात एक जैसी वृत्ताकार समतल डिस्को , जिनमें प्रत्येक का द्रव्यमान M तथा त्रिज्या R है , को सममित रूप से जोड़ा जाता है । समतल के लंबवत तथा P से गुजरने वाली अक्ष के सापेक्ष , इस संयोजन का जड़त्व आघूर्ण है -
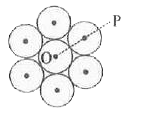
View SolutionR त्रिज्या तथा 9 M द्रव्यमान की एक वृत्तीय चकती se R/3 त्रिजा की एक छोरी चाक्ति काटी जाती है । चकति के तल के लंबवत तथा O से गुजरते वाली तथा अक्ष के प्रीत: शेष चक्ति का जड़त्व आघूर्ण होगा -
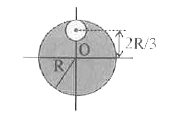
View Solutionकिसी दृढ़ छड़ की लम्बाई L है और उसका द्रव्यमान नगण्य है । इसके दो विपरीत सिरों पर क्रमश : `m_(1)` तथा `m_(2)` द्रव्यमान के दो बिंदु पिंड रखे गये हैं इस छड़ को उसके स्वयं के लंबवत अक्ष के परित घुर्णन करना है जो छड़ पर स्थित किसी बिंदु P से होकर गुजरती है । तो बिंदु P की वह स्थिति जिसके लिए छड़ को कोणीय वेग `omega_(0)` से घूर्ण करने के लिए आवश्यक कार्य न्यूनतम होगा कौन सी है -
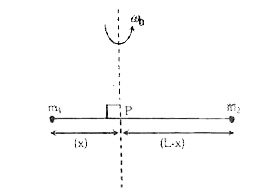
View Solutionकिसी ठोस गोले द्रव्यमान M तथा इसकी त्रिज्या R है । इसमें से अधिकतम संभव आयतन का एक क्यूब काट लिया जाता है इस क्यूब का जड़त्व आघूर्ण कितना होगा , यदि इसका पूर्ण अक्ष इसके केंद्र से होकर गुजरता है तथा इसके किसी एक फलक के लंबवत है -
View Solutionएक घर्षणहीन बेयरिंग पर एक घिरनी के चरों ओर एक डोरी को लपेट क्र द्रव्यमान m लटकाया गया है । घिरनी का द्रव्यमान m और त्रिज्या R है । यह मान लें की घिरनी एक पूर्ण एकसमान वृत्तीय चकती है । यदि डोरी घिरनी पर फिसलती नहीं है , तब द्रव्यमान m का त्वरण है -
View Solutionएक मोटर वाहन किसी सड़क पर `54 kmh^(-1)` की छाल से चल रहा है । इसके पहियों की त्रिज्या 0.45 m और घूर्णन अक्ष के प्रिट का जड़त्व आघूर्ण `3 gm^(2)` है यदि वाहन 15s में विराम अवस्था में आये तब ब्रेक द्वारा पहिए पर लगा ओसात बल आघूर्ण का मान होगा
View Solutionएक समरूप छड़ AB की लम्बाई l तथा द्र्वयमान m है , यह बिंदु A के परित घूर्णन के लिए स्वतंत्र है । क्षैतिज स्थिति में विराम से छड़ को छोड़ा जाता है । छड़ का A के परित : जड़त्व आघूर्ण `(ml^(2))/(3)` हो तब का प्रारम्भिक कोणीय त्वरण होता -

View Solutionएक छल्ला जिसका द्रव्यमान M तथा त्रिज्या R है केंद्र O से होकर जाने वाले स्थिर उध्र्वाधर अक्ष के चारों ओर (i) कोणीय गति से घूम रहा है । स समय पर `(M)/(8)` द्रव्यमान के दो बिंदु द्रव्यमान छल्ले के केंद्र O पर विराम स्थिति में हैं । वे चित्र में दर्शाए अनुसार छल्ले पर लगी द्रव्यमान रहित दो छड़ों के त्रिजात: बहार की ओर गति कर सकते हैं । किसी एक क्षण पर निकाय की कोणीय गति `(8)/(9) omega` तथा एक द्रव्यमान O से `(3)/(5)` की दूरी पर है । इस क्षण दूसरे बिंदु द्रव्यमान की O से दूरी होती -
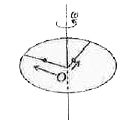
View Solutionलम्बाई l की एक अवितंय डोरी से बंधे द्र्व्यमान m के एक बाब को एक ऊर्ध्वाधर आधार से लटकाया जाता है । बाब ऊर्ध्वाधर पर कोणीय चाल `omega` d/s से एक क्षैतिज वृत्त में घूर्णन करता है । निलंबन बिंदु पर -
View Solutionघूर्णन करते हुए दो पिंडों A तथा B के द्रव्यमान क्रमश : m तथा 2m और जड़त्व आघूर्ण क्रमश : `I_(A)` तथा `I_(B) (I_(B) > I_(A))` है । दोनों की घूर्णन गतिज ऊर्जाएं बराबर हैं । यदि इसके कोणीय क्रमश `L_(A)` तथा `L_(B)` हो तब -
View Solutionद्रव्यमान M तथा त्रिज्या R का एक ठोस गोला अपने व्यास के परित घूर्णन कर रहा है । उसी द्रव्यमान तथा उसी त्रिज्या का एक ठोस बेलन भी अपने ज्यामितीय अक्ष के परित घूर्णन कर रहा है । बेलन के घूर्णन की कोणीय चाल गोले से दोगुना है । इन दोनों की घूर्णन गतिज ऊर्जाओं का अनुपात `(E_( गोला ) // E_( बेलन ))` होगा -
View Solutionकोई डिरक और कोई गोला जिनकी त्रिज्याएँ समान परन्तु द्रव्यमान भिन्न है समान उन्नतांश और लम्बाई के दो आनत समतलों पर लुढ़कते हैं । इन दोनों पिंडों में से तली तक पहले कौन पहुंचेगा -
View Solutionएक ठोस गोला लोटन गति में है । लोटन गति में वास्तु की स्थानंतरीय गति ऊर्जा `(K_(t)` के साथ -साथ घूर्णी गतिज ऊर्जा `(K_(r ))` भी होती है । गोले के लिए `K_(t) : (K_(t) + K_(r ))` का अनुपात होगा -
View Solutionएक समतल को पीछे से साफ़ करने की एक मशीन द्वारा R त्रिजा के पीछे को कुल ऊर्ध्वाधर बल F से दबाकर उसे उसकी अक्ष के परित एक नियत कोणीय गति से घुमाया जाता है । यदि बल F पीछे पर एकसमान वितरित है तथा पीछे तथा समतल के बीच ghrshn गुणांक `mu` है तो मशीन द्वारा पीछे पर लगाया गया बल आघूर्ण होगा -
View Solutionएक द्रव्यमान रहित तथा 3l की छड़ पर दो द्र्व्यमान चित्रानुसार उसके सिरों पर लगाएं हैं तथा उसे एक क्षैतिज अक्ष पर बिंदु P से कीलकित जाता है । जब इस छड़ को क्षैतिज अवस्था से छोड़ा जाता है तो उसका तात्क्षणिक त्वरण होगा -

View Solutionचित्रानुसार 20 g द्रव्यमान के एक कण को 5m/s व वक्र के अनुगत प्रारंभिक वेग से बिंदु A से छोड़ा जाता है । बिंदु A की बिंदु B से ऊंचाई h है । यह कण घर्षणहीन पृष्ठ पर सरकता है। जब कण बिन्दु B पर पहुंचता है , तो इसका बिंदु O के सापेक्ष कोणीय संवेग क्या होगा -
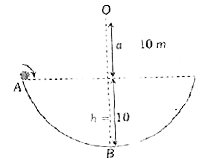
View Solutionद्रव्यमान M तथा लम्बाई L की एक पतली छड़ कोणीय चाल `omega_(0)` से छड़ के लंबवत तथा उसके केंद्र से जाने वाली अक्ष आकार की स्वतंत्र रूप से घूम रही है । द्रव्यमान m तथा नगण्य आकर की दो महिकारों आरम्भ में छड़ ke केंद्र पर है । यह मणिकाएँ छड़ पर चलने को स्वतंत्र हैं । अमिकाएँ जब छड के विपरीत सिरों पर पहुंचती है तो इस विन्यास को कोणीय छल होगी -
View Solutionद्रव्यमान M तथा त्रिज्या R के एक ठोस गोले को दो आसमान हिस्सों में बाँटा जाता है ।
View Solution`(7M)/(8)` द्रव्यमान के पहले हिस्से को एक 2R त्रिज्या की एकसमान डिस्क में बदला जाता है । बचे हुए हिस्से से एक एकसमान ठोस गोला बनाया जाता है । मानाकि `I_(1)` डिस्क का उसकी अक्ष के परित जड़त्व आघूर्ण है तथा `I_(2)` नये गोले का उसके अक्ष के परित जड़त्व आघूर्ण है । अनुपात `I_(1)//I_(2)` होगा -
View Solutionद्रव्यमान m के एक कण की स्थितिज ऊर्जा `V (r ) = kr^(2) //2` है , जहाँ r एक नियत बिंदु O से कण की दूरी है और K उचित विमाओं वाला एक धनात्मक नियतांक है । यह कण बिंदु O के सापेक्ष R त्रिज्या वाली एक वृत्तीय कक्ष में घूम रहा है । यदि V कण की चाल है और L बिंदु Q के सापेक्ष इसके कोणीय संवेग का परिमाण है , तो निम्नलिखित कथनों में से कौन सा नहीं है -
View Solutionएक वृत्तकर वलय और एक वृत्तकर चकती एक आनंत ताल के शीर्ष पर अलग-अलग वीरामवस्था में है आनंत तल क्षैतिज तल से `60^(@)` का कोण बनाता है । दोनों वस्तुएँ एक ही पल न्यूनतम दूरी वाले पथ पर बिना फ़िसले लोटना आरम्भ करती हैं । यदि दोनों वस्तुओं का क्षैतिज तल पर पहुंचने का समयांतर `(2 - sqrt(3))//sqrt(10)` हो , तो आनंत तल के शीर्ष की ऊंचाई .... मीटर में । `(g = 10 ms^(-2))` लें ।
View Solutionएक L लम्बाई का दृढ़ दंड AB अपनी ऊर्ध्वाधर स्थिति से घर्षणहीन अनुभूमिका तल पर चित्रानुसार फिसल रहा है । समय के किसी क्षण पर दंड ऊर्ध्वाधर से बनाया कोण `theta` है । निम्न में से कौन सा प्रकथन सही है -
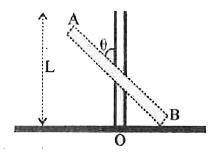
View Solutionऊर्ध्वाधर धुरी पर दो चकती A तथा B को समक्ष रूप से लगाया गया है । चकती के जड़त्व आघूर्ण उभयनिष्ठ अक्ष के परित क्रमश : I तथा 2I है । स्प्रिंग को `x_(1)` दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग `2 omega` प्राप्त करती है । समान स्प्रिंग नियतांक की स्प्रिंग को `x_(2)` दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग `omega` प्राप्त करती है । दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है ।
उपरोक्त प्रक्रम में गतिज ऊर्जा का क्षय है -
View Solutionऊर्ध्वाधर धुरी पर दो चकती A तथा B को समक्ष रूप से लगाया गया है । चकती के जड़त्व आघूर्ण उभयनिष्ठ अक्ष के परित क्रमश : I तथा 2I है । स्प्रिंग को `x_(1)` दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग `2 omega` प्राप्त करती है । समान स्प्रिंग नियतांक की स्प्रिंग को `x_(2)` दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग `omega` प्राप्त करती है । दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है ।
जब चकती B को चकती A के सम्पर्क में किया जाता है , तब ये समय t में उभयनिष्ठ कोणीय वेग प्राप्त कर लेती है । इस समय अंतराल में एक चकती द्वारा दूसरी से प्राप्त औसत घर्षण बल आघूर्ण है -
View Solutionऊर्ध्वाधर धुरी पर दो चकती A तथा B को समक्ष रूप से लगाया गया है । चकती के जड़त्व आघूर्ण उभयनिष्ठ अक्ष के परित क्रमश : I तथा 2I है । स्प्रिंग को `x_(1)` दूरी तक सम्पीड़ित करने से प्राप्त सम्पूर्ण स्थितिज ऊर्जा से चकती A प्रारम्भिक कोणीय वेग `2 omega` प्राप्त करती है । समान स्प्रिंग नियतांक की स्प्रिंग को `x_(2)` दूरी तक सम्पीड़ित करने से चकती B कोणीय वेग `omega` प्राप्त करती है । दोनों चकतियाँ दक्षिणावर्त दिशा में घूर्णन करती है । <,बर>, अनुपात `x_(1)//x_(2)` है -
View Solution
गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न questions and complete solutions for chapter कणों के निकाय तथा घूर्णी गति of SANJEEV PUBLICATION of Class 11
All Exercises from SANJEEV PUBLICATION Class 11 PHYSICS कणों के निकाय तथा घूर्णी गति
- अन्य महत्वपूर्ण प्रश्न - अतिलघुत्तरात्मक प्रश्न
- अन्य महत्वपूर्ण प्रश्न - कॉलम A से कॉलम B का सही मिलान कीजिए -
- अन्य महत्वपूर्ण प्रश्न - निबन्धात्मक प्रश्न
- अन्य महत्वपूर्ण प्रश्न - रिक्त स्थान की पूर्ति
- अन्य महत्वपूर्ण प्रश्न - लघुत्तरात्मक प्रश्न
- अन्य महत्वपूर्ण प्रश्न - सत्य/असत्य
- अन्य महत्वपूर्ण प्रश्न -बहुविकल्पी प्रश्न
- अन्य महत्वपूर्ण प्रश्न - आंकिक प्रश्न
- उदाहरण
- गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न
- पाठ्यपुस्तक के प्रश्न