Complete Solutions to अभ्यास (पाठ्यपुस्तक (NCERT) के प्रश्न ) of chapter अणुगति सिध्दान्त of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | अणुगति सिध्दान्त |
| SANJEEV PUBLICATION | अभ्यास (पाठ्यपुस्तक (NCERT) के प्रश्न ) |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
ऑक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गये कुल आयतन का अनुपात ज्ञात कीजिये। ऑक्सीजन के एक अणु का व्यास `3A` लीजिये।
View Solutionमोलर आयतन STP पर किसी गैस (आदर्श ) के 1 मोल द्वारा घेरा गया है। आयतन है। (STP : 1 atm दाब `0^(@)C` ) दर्शाइये कि यह 22.4 लीटर है।
View Solutionचित्र में ऑक्सीजन के `1.00 xx 10^(-3)` kg द्रव्यमान लिये`PV//T` एवं P में दो अलग – अलग तापों पर ग्राफ दर्शाये गये है।
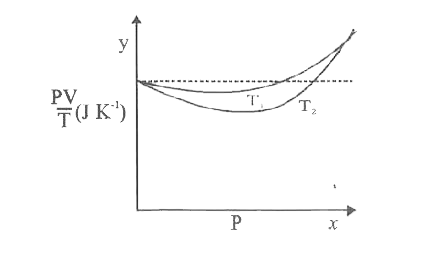
(a) बिंदुकित रेखा क्या य दर्शाती है।
(b) क्या सत्य है। `T_(1) gt T_(2) "अथवा" T_(1) lt T_(2) ?`
(c ) अक्ष पर जहॉ। मिलते है। वहाँ `PV//T` का मान क्या है।
(d) यदि हम ऐसे ही ग्राफ `1.00 xx 10^(3) kg` हाइड्रोजन के लिए बनाऍं तो भी क्या उस बिंदु पर जहाँ तक्र y-अक्ष से मिलते है। `PV//T` का मान कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा। `H_(2)` का अणु द्रव्यमान `=2.02 u O_(2)` का द्रव्यमान
`=32.u ,R = 8,31 J mol^(-1) K^(-1)`
View Solutionएक ऑक्सीजन सिलिंडर जिसका आयतन 30 लीटर है में ऑक्सीजन का आरंभिक दाब 15 atm एवं ताप `27^(@)C` है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी दाब गिर कर 11 atm एवं ताप गिर कर `17^(@)C` हो जाता हैं ज्ञात कीजिए। कि सिलिंडर से ऑकसीजन की कितनी मात्रा निकाली गई है।
`(R= 8.31 J mol^(-1) K^(-1)` ऑक्सीजन का अणु द्रव्यमान `O_(2) = 32 u`) ।
View Solutionवायु का एक बुलबुला जिसका आयतन `1.0cm^(3)` बाहरी झील की तली से जहाँ ताप `12^(@)C` है। उठकर ऊपर जाता हैं जहाँ ताप `35^(@)C` हैं अब इसका आयतन क्या होगा।
View Solution,एक कमरे में जिसका आयतन `25.0m^(3)` है। `27^(@)C` ताप और 1atm दाब पर वायु के कुल अणुओं (जिनमें नाइट्रोजन , ऑक्सीजन , जलवाष्प ओर अन्य सभी अवयवों के कण सम्मिलित है। ) की संख्या ज्ञात कीजिए।
View Solutionहीलियम परमाणु की औसत तापीय ऊर्जा का आकलन कीजिये। (i) कमरे के ताप `(27^(@)C)`पर । (ii) सूर्य के पृष्ठीय ताप `(600 K)` पर। (iii) 100 लाख केल्विन ताप (तारे के क्रोड का प्रारूपिक ताप ) पर।
View Solutionसमान धरिता के तीन बर्तनों में एक ही ताप और दाब पर गैसे भरी है। पहले बर्तन में नियाँन गैस है। दूसरे में क्लोरीन गैस है और तीसरे में यूरेनियम हैक्साफलोराइड गेस है। क्या तीनो बर्तनो में गैसों के संगत अणुओ की संख्या समान हैं क्या तीनो प्रकारणों में अणुओं की
`V_(rms)` (वर्ग माध्य मूल चाल ) समान हैं
View Solutionकिस ताप पर आर्गन गैस सिलिंडर में अणुओं की `C_(rms) – 20^(@)C` पर हीलियम गैस परमाणुओं की `c_(rms) ` के बराबर होगी।
(Ar का परमाणु द्रव्यमान =39.9u एवं हीलियम का परमाणु द्रव्यमान =4.0 u)
View Solutionनाइट्रोजन गैस के एक सिलिंडर में 2.0 atm दाब एवं `170^(@)C` ताप पर , नाइट्रोजन अणुओं के माध्य मुक्त पथावं संघटट आवृति का आकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग `1.0A` लिजिए। संघट – काल की तुलना अणुओं द्वारा दो संघटटों के बीच स्वतंत्रातापूर्वक चलने में लगे समय से कीजिए। । (नाइट्रोजन आण्विक द्रवव्यमान =28.0 u )।
View Solutionएक मीटर लंबी सँकरी (और एक सिरे पर बंद ) नली क्षेतिज रखी गई । इसमें 76cm लंबाई भरा पारद सूत्र वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा। सय यदि खुला सिरा नीचे की और रखते हुए नली को ऊर्ध्वाधर कर दिया जाए।
View Solutionकिसी उपकरण से हाइड्रोजन गैस `28.7 cm^(3) s^(-1)` की दर से विसरित हो रही हैं उन्ही स्थितियों में कोई दूसरी गैस `7.2 cm^(3) s^(-1)` की दर से विसरित होती है। इस दूसरी गैस को पहचानिए।
[संकेत : ग्राहम के विरण नियम `R_(1)// R_(2) = (M_(2) //M_(1))^(1//2)` का उपयोग कीजिए यहाँ `R_(1), R_(2)` क्रमश: गैसों की विसरण दर तथा `m_(1) ` एवं `m_(2)` उनके आण्विक द्रव्यमान है यह नियम अणुगति सिध्दांत का एक सरल परिणाम है।]
View Solutionसाम्यवस्था में किसी गैस का घनत्व और दाब अपने सम्पूर्ण आयतन में एकसमान है यह पूर्णतया सत्य केवल तभी है। जब किसी गैस स्तभ का घनत्व एकमसान नही होता हैं जैसा निभरता वातारण के नियम `n_(2)= n_(1) exp [-(mg)/( k_(B) T) (h_(2) = h_(1))]` से दी जाती है। `n_(2) ,n_(1)` क्रमश: `h_(1)` व`h_(1)` ऊँचाईयों पर संख्यात्मक निलंबित किसी कण के अवसादन साम्य के लिए समीकरण
लिए कीजिए यहाँ p निलंबित कण का घनत्व तथाp चारों तरफ के माध्यम का घनतव है। `N_(A)` आवोगाद्रो संख्या तथा R सार्वत्रिक गैस नियंतांक है। [संकेत : निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिध्दात का उपयोग कीजिए।]
View Solutionनीचे कुछ ठोसें व द्रवों के घनत्व दिए गए है। उनके परमाणुओं की आमापों का आकलन कीजिए।
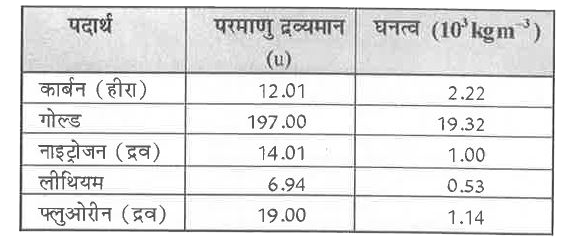
[संकेत : मान लीजिए कि परमाणु ठोस अथवा द्रव् प्रावस्था में द्रढुता से बँधे है तथा आवोगद्रो संख्या के ज्ञात मान का उपयोग कीजिए। प्रयोग नही करना चाहिए। क्योकि दृढ़ संवेष्टन सन्निकटन की रूक्षात के परमाणवीय आकार कुछ A के परासर है। ]
View Solutionऑक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गये कुल आयतन का अनुपात ज्ञात कीजिये। ऑक्सीजन के एक अणु का व्यास `3A` लीजिये।
View Solutionमोलर आयतन STP पर किसी गैस (आदर्श ) के 1 मोल द्वारा घेरा गया है। आयतन है। (STP : 1 atm दाब `0^(@)C` ) दर्शाइये कि यह 22.4 लीटर है।
View Solutionचित्र में ऑक्सीजन के `1.00 xx 10^(-3)` kg द्रव्यमान लिये`PV//T` एवं P में दो अलग – अलग तापों पर ग्राफ दर्शाये गये है।

(a) बिंदुकित रेखा क्या दर्शाती है?
(b) क्या सत्य है? `T_(1) gt T_(2) "अथवा" T_(1) lt T_(2) ?`
(c ) अक्ष पर जहाँ वक्र मिलते है वहाँ `PV//T` का मान क्या है।
(d) यदि हम ऐसे ही ग्राफ `1.00 xx 10^(3) kg` हाइड्रोजन के लिए बनाऍं तो भी क्या उस बिंदु पर जहाँ तक्र y-अक्ष से मिलते है। `PV//T` का मान कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा। `H_(2)` का अणु द्रव्यमान `=2.02 u O_(2)` का द्रव्यमान
`=32.u ,R = 8,31 J mol^(-1) K^(-1)`
View Solutionएक ऑक्सीजन सिलिंडर जिसका आयतन 30 लीटर है में ऑक्सीजन का आरंभिक दाब 15 atm एवं ताप `27^(@)C` है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी दाब गिर कर 11 atm एवं ताप गिर कर `17^(@)C` हो जाता हैं ज्ञात कीजिए। कि सिलिंडर से ऑकसीजन की कितनी मात्रा निकाली गई है।
`(R= 8.31 J mol^(-1) K^(-1)` ऑक्सीजन का अणु द्रव्यमान `O_(2) = 32 u`) ।
View Solutionवायु का एक बुलबुला जिसका आयतन `1.0cm^(3)` बाहरी झील की तली से जहाँ ताप `12^(@)C` है। उठकर ऊपर जाता हैं जहाँ ताप `35^(@)C` हैं अब इसका आयतन क्या होगा।
View Solution,एक कमरे में जिसका आयतन `25.0m^(3)` है। `27^(@)C` ताप और 1atm दाब पर वायु के कुल अणुओं (जिनमें नाइट्रोजन , ऑक्सीजन , जलवाष्प ओर अन्य सभी अवयवों के कण सम्मिलित है। ) की संख्या ज्ञात कीजिए।
View Solutionहीलियम परमाणु की औसत तापीय ऊर्जा का आकलन कीजिये। (i) कमरे के ताप `(27^(@)C)`पर । (ii) सूर्य के पृष्ठीय ताप `(600 K)` पर। (iii) 100 लाख केल्विन ताप (तारे के क्रोड का प्रारूपिक ताप ) पर।
View Solutionसमान धरिता के तीन बर्तनों में एक ही ताप और दाब पर गैसे भरी है। पहले बर्तन में नियाँन गैस है। दूसरे में क्लोरीन गैस है और तीसरे में यूरेनियम हैक्साफलोराइड गेस है। क्या तीनो बर्तनो में गैसों के संगत अणुओ की संख्या समान हैं क्या तीनो प्रकारणों में अणुओं की
`V_(rms)` (वर्ग माध्य मूल चाल ) समान हैं
View Solutionकिस ताप पर आर्गन गैस सिलिंडर में अणुओं की `C_(rms) – 20^(@)C` पर हीलियम गैस परमाणुओं की `c_(rms) ` के बराबर होगी।
(Ar का परमाणु द्रव्यमान =39.9u एवं हीलियम का परमाणु द्रव्यमान =4.0 u)
View Solutionनाइट्रोजन गैस के एक सिलिंडर में 2.0 atm दाब एवं `170^(@)C` ताप पर , नाइट्रोजन अणुओं के माध्य मुक्त पथावं संघटट आवृति का आकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग `1.0A` लिजिए। संघट – काल की तुलना अणुओं द्वारा दो संघटटों के बीच स्वतंत्रातापूर्वक चलने में लगे समय से कीजिए। । (नाइट्रोजन आण्विक द्रवव्यमान =28.0 u )।
View Solutionएक मीटर लंबी सँकरी (और एक सिरे पर बंद ) नली क्षेतिज रखी गई । इसमें 76cm लंबाई भरा पारद सूत्र वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा। सय यदि खुला सिरा नीचे की और रखते हुए नली को ऊर्ध्वाधर कर दिया जाए।
View Solutionकिसी उपकरण से हाइड्रोजन गैस `28.7 cm^(3) s^(-1)` की दर से विसरित हो रही हैं उन्ही स्थितियों में कोई दूसरी गैस `7.2 cm^(3) s^(-1)` की दर से विसरित होती है। इस दूसरी गैस को पहचानिए।
[संकेत : ग्राहम के विरण नियम `R_(1)// R_(2) = (M_(2) //M_(1))^(1//2)` का उपयोग कीजिए यहाँ `R_(1), R_(2)` क्रमश: गैसों की विसरण दर तथा `m_(1) ` एवं `m_(2)` उनके आण्विक द्रव्यमान है यह नियम अणुगति सिध्दांत का एक सरल परिणाम है।]
View Solutionसाम्यवस्था में किसी गैस का घनत्व और दाब अपने सम्पूर्ण आयतन में एकसमान है यह पूर्णतया सत्य केवल तभी है। जब किसी गैस स्तभ का घनत्व एकमसान नही होता हैं जैसा निभरता वातारण के नियम `n_(2)= n_(1) exp [-(mg)/( k_(B) T) (h_(2) = h_(1))]` से दी जाती है। `n_(2) ,n_(1)` क्रमश: `h_(1)` व`h_(1)` ऊँचाईयों पर संख्यात्मक निलंबित किसी कण के अवसादन साम्य के लिए समीकरण
लिए कीजिए यहाँ p निलंबित कण का घनत्व तथाp चारों तरफ के माध्यम का घनतव है। `N_(A)` आवोगाद्रो संख्या तथा R सार्वत्रिक गैस नियंतांक है। [संकेत : निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिध्दात का उपयोग कीजिए।]
View Solutionनीचे कुछ ठोसें व द्रवों के घनत्व दिए गए है। उनके परमाणुओं की आमापों का आकलन कीजिए।

[संकेत : मान लीजिए कि परमाणु ठोस अथवा द्रव् प्रावस्था में द्रढुता से बँधे है तथा आवोगद्रो संख्या के ज्ञात मान का उपयोग कीजिए। प्रयोग नही करना चाहिए। क्योकि दृढ़ संवेष्टन सन्निकटन की रूक्षात के परमाणवीय आकार कुछ A के परासर है। ]
View Solutionऑक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गये कुल आयतन का अनुपात ज्ञात कीजिये। ऑक्सीजन के एक अणु का व्यास `3A` लीजिये।
View Solutionमोलर आयतन STP पर किसी गैस (आदर्श ) के 1 मोल द्वारा घेरा गया है। आयतन है। (STP : 1 atm दाब `0^(@)C` ) दर्शाइये कि यह 22.4 लीटर है।
View Solutionचित्र में ऑक्सीजन के `1.00 xx 10^(-3)` kg द्रव्यमान लिये`PV//T` एवं P में दो अलग – अलग तापों पर ग्राफ दर्शाये गये है।

(a) बिंदुकित रेखा क्या दर्शाती है?
(b) क्या सत्य है? `T_(1) gt T_(2) "अथवा" T_(1) lt T_(2) ?`
(c ) अक्ष पर जहाँ वक्र मिलते है वहाँ `PV//T` का मान क्या है।
(d) यदि हम ऐसे ही ग्राफ `1.00 xx 10^(3) kg` हाइड्रोजन के लिए बनाऍं तो भी क्या उस बिंदु पर जहाँ तक्र y-अक्ष से मिलते है। `PV//T` का मान कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा। `H_(2)` का अणु द्रव्यमान `=2.02 u O_(2)` का द्रव्यमान
`=32.u ,R = 8,31 J mol^(-1) K^(-1)`
View Solutionएक ऑक्सीजन सिलिंडर जिसका आयतन 30 लीटर है में ऑक्सीजन का आरंभिक दाब 15 atm एवं ताप `27^(@)C` है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी दाब गिर कर 11 atm एवं ताप गिर कर `17^(@)C` हो जाता हैं ज्ञात कीजिए। कि सिलिंडर से ऑकसीजन की कितनी मात्रा निकाली गई है।
`(R= 8.31 J mol^(-1) K^(-1)` ऑक्सीजन का अणु द्रव्यमान `O_(2) = 32 u`) ।
View Solutionवायु का एक बुलबुला जिसका आयतन `1.0cm^(3)` बाहरी झील की तली से जहाँ ताप `12^(@)C` है। उठकर ऊपर जाता हैं जहाँ ताप `35^(@)C` हैं अब इसका आयतन क्या होगा।
View Solution,एक कमरे में जिसका आयतन `25.0m^(3)` है। `27^(@)C` ताप और 1atm दाब पर वायु के कुल अणुओं (जिनमें नाइट्रोजन , ऑक्सीजन , जलवाष्प ओर अन्य सभी अवयवों के कण सम्मिलित है। ) की संख्या ज्ञात कीजिए।
View Solutionहीलियम परमाणु की औसत तापीय ऊर्जा का आकलन कीजिये। (i) कमरे के ताप `(27^(@)C)`पर । (ii) सूर्य के पृष्ठीय ताप `(600 K)` पर। (iii) 100 लाख केल्विन ताप (तारे के क्रोड का प्रारूपिक ताप ) पर।
View Solutionसमान धरिता के तीन बर्तनों में एक ही ताप और दाब पर गैसे भरी है। पहले बर्तन में नियाँन गैस है। दूसरे में क्लोरीन गैस है और तीसरे में यूरेनियम हैक्साफलोराइड गेस है। क्या तीनो बर्तनो में गैसों के संगत अणुओ की संख्या समान हैं क्या तीनो प्रकारणों में अणुओं की
`V_(rms)` (वर्ग माध्य मूल चाल ) समान हैं
View Solutionकिस ताप पर आर्गन गैस सिलिंडर में अणुओं की `C_(rms) – 20^(@)C` पर हीलियम गैस परमाणुओं की `c_(rms) ` के बराबर होगी।
(Ar का परमाणु द्रव्यमान =39.9u एवं हीलियम का परमाणु द्रव्यमान =4.0 u)
View Solutionनाइट्रोजन गैस के एक सिलिंडर में 2.0 atm दाब एवं `170^(@)C` ताप पर , नाइट्रोजन अणुओं के माध्य मुक्त पथावं संघटट आवृति का आकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग `1.0A` लिजिए। संघट – काल की तुलना अणुओं द्वारा दो संघटटों के बीच स्वतंत्रातापूर्वक चलने में लगे समय से कीजिए। । (नाइट्रोजन आण्विक द्रवव्यमान =28.0 u )।
View Solutionएक मीटर लंबी सँकरी (और एक सिरे पर बंद ) नली क्षेतिज रखी गई । इसमें 76cm लंबाई भरा पारद सूत्र वायु के 15 cm स्तंभ को नली में रोककर रखता है। क्या होगा। सय यदि खुला सिरा नीचे की और रखते हुए नली को ऊर्ध्वाधर कर दिया जाए।
View Solutionकिसी उपकरण से हाइड्रोजन गैस `28.7 cm^(3) s^(-1)` की दर से विसरित हो रही हैं उन्ही स्थितियों में कोई दूसरी गैस `7.2 cm^(3) s^(-1)` की दर से विसरित होती है। इस दूसरी गैस को पहचानिए।
[संकेत : ग्राहम के विरण नियम `R_(1)// R_(2) = (M_(2) //M_(1))^(1//2)` का उपयोग कीजिए यहाँ `R_(1), R_(2)` क्रमश: गैसों की विसरण दर तथा `m_(1) ` एवं `m_(2)` उनके आण्विक द्रव्यमान है यह नियम अणुगति सिध्दांत का एक सरल परिणाम है।]
View Solutionसाम्यवस्था में किसी गैस का घनत्व और दाब अपने सम्पूर्ण आयतन में एकसमान है यह पूर्णतया सत्य केवल तभी है। जब किसी गैस स्तभ का घनत्व एकमसान नही होता हैं जैसा निभरता वातारण के नियम `n_(2)= n_(1) exp [-(mg)/( k_(B) T) (h_(2) = h_(1))]` से दी जाती है। `n_(2) ,n_(1)` क्रमश: `h_(1)` व`h_(1)` ऊँचाईयों पर संख्यात्मक निलंबित किसी कण के अवसादन साम्य के लिए समीकरण
लिए कीजिए यहाँ p निलंबित कण का घनत्व तथाp चारों तरफ के माध्यम का घनतव है। `N_(A)` आवोगाद्रो संख्या तथा R सार्वत्रिक गैस नियंतांक है। [संकेत : निलंबित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिध्दात का उपयोग कीजिए।]
View Solutionनीचे कुछ ठोसें व द्रवों के घनत्व दिए गए है। उनके परमाणुओं की आमापों का आकलन कीजिए।

[संकेत : मान लीजिए कि परमाणु ठोस अथवा द्रव् प्रावस्था में द्रढुता से बँधे है तथा आवोगद्रो संख्या के ज्ञात मान का उपयोग कीजिए। प्रयोग नही करना चाहिए। क्योकि दृढ़ संवेष्टन सन्निकटन की रूक्षात के परमाणवीय आकार कुछ A के परासर है। ]
View Solution
अभ्यास (पाठ्यपुस्तक (NCERT) के प्रश्न ) questions and complete solutions for chapter अणुगति सिध्दान्त of SANJEEV PUBLICATION of Class 11
All Exercises from SANJEEV PUBLICATION Class 11 PHYSICS अणुगति सिध्दान्त
- अन्य महत्त्वपूर्ण प्रश्न (अतिलघूत्तरात्मक प्रश्न)
- अन्य महत्त्वपूर्ण प्रश्न (आंकिक प्रश्न )
- अन्य महत्त्वपूर्ण प्रश्न (कॉलम)
- अन्य महत्त्वपूर्ण प्रश्न (निबन्धात्मक प्रश्न )
- अन्य महत्त्वपूर्ण प्रश्न (बहुचयनात्मक प्रश्न )
- अन्य महत्त्वपूर्ण प्रश्न (रिक्त स्थानों की प्रूर्ति कीजिए। )
- अन्य महत्त्वपूर्ण प्रश्न (लघूत्तरात्मक प्रश्न )
- अन्य महत्त्वपूर्ण प्रश्न (सत्य / असत्य )
- अभ्यास (पाठ्यपुस्तक (NCERT) के प्रश्न )
- उदाहरण
- गत वर्षो की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न