Complete Solutions to अभयास (पाठ्यपुस्तक के प्रश्न) of chapter दोलन of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | दोलन |
| SANJEEV PUBLICATION | अभयास (पाठ्यपुस्तक के प्रश्न) |
| Number Of Questions | 25 |
| Academic Year | 2023-24 |
नीचे दिये गये उदाहरणों में कौन आवर्ती गति को निरूपित करता है?
(i) किसी तैराक द्वारा नदी के एक तट से दूसरे तट तक जाना और अपनी एक वापसी यात्रा पूरी करना।
(ii) किसी स्वतंत्रतापूर्वक लटकाये गये दंडचुम्बक को उसकी N-S दिशा से विस्थापित कर छोड़ देना।
(iii) अपने द्रव्यमान केन्द्र के परितः घूर्णी गति करता कोई हाइड्रोजन अणु।
(iv) किसी कमान से छोड़ा गया तीर।
View Solutionनीचे दिये गये उदाहरणों में कौन (लगभग) सरल आवर्त गति को तथा कौन आवर्ती परन्तु सरल आवर्त गति निरूपित नहीं करते हैं?
(i) पृथ्वी की अपने अक्ष के परितः घूर्णन गति।
(ii) किसी U नली में दोलायमान पारे के स्तम्भ की गति।
(iii) किसी चिकने वक्रीय कटोरे के भीतर एक बॉल बियरिंग की गति जब उसे निम्नतम बिन्दु से कुछ ऊपर के बिन्दु से मुक्त रूप से छोड़ा जाये।
(iv) किसी बहु परमाणुक अणु की अपनी साम्यावस्था की स्थिति के परितः व्यापक कम्पन।
View Solutionचित्र में किसी कण की रैखिक गति के लिये चार :आरेख दिये गये हैं। इनमें से कौन-सा आरेख आवर्ती गति का निरूपण करता है? उस गति काआवर्तकाल क्या है (आवर्ती गति वाली गति का)
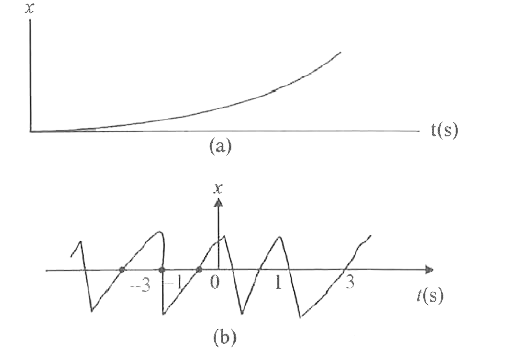
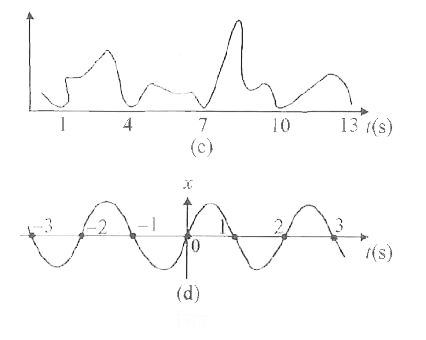
View Solutionनीचे दिये गये समय के फलनों में कौनसा
(a) सरल आवर्त गति
(b) आवर्ती परन्तु सरल आवर्त गति नहीं, तथा
(c) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिये:(`omega` कोई धनात्मक अचर है।)
(a) `sinomegat-cosomegat`
(b) `sin^(3)omegat`
(c) `3cos(pi/4 - 2omegat`
(d) `cosomegat + cos3omegat + cos5omegat`
(e) `exp(-omega^(2)t^(2))
(f)`1 + omegat + omega^(2)t^(2)`
View Solutionकोई कण एक दूसरे से 10 सेमी. दूरी पर स्थित दो बिन्दुओं तथा B के बीच रैखिक सरल आवतं गति कर रहा है। A से 8 की ओर की दिशा को धनात्मक दिशा मानकर वेग, त्वरण तथा कण पर लगे बल के चिन्ह ज्ञात कीजिये जबकि यह कण
(a)Aसिरे पर है
(b) B सिरे पर है
(c)A की ओर जाते हुए AB के मध्य बिन्दु पर है।
(d)A की ओर जाते हुए B से 2 सेमी. दूर है।
(e)B की ओर जाते हुए A से 3 सेमी. दूर है तथा
(f) A की ओर जाते हुए Bसे 4 सेमी. दूर है।
View Solutionनीचे दिये गये किसी कण के त्वरण a तथा विस्थापन x के बीच संबंधों में से किससे सरल आवर्त गति संबद्ध है
(a) a = 0.7x
(b) a = -`200x^(2)`
(c) a = -10x
(d) `a= 100x^(3)`
View Solutionसरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिये गये विस्थापन फलन द्वारा किया जाता है,
`x(t) = Acos (omegat+phi)` यदि कण की आरंभिक (t=0) स्थिति 1 सेमी. तथा उसका आरम्भिक वेग `pi` cm/s है, तो कण का आयाम तथा आरंभिक कला कोण क्या है? कण की कोणीय आवृत्ति `pi//s` है। यदि सरल आवर्त गति का वर्णन करने के लिये कोज्या (cos) फलन के स्थान पर हम ज्या (sin) फलन चुनें, `x=B sin (omegat+alpha)` तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा?
View Solutionकिसी कमानीदार तुला का पैमाना 0 से 50 kg तक अंकित है और पैमाने की लंबाई 20 cm है। इस तुला से लटकाया गया कोई पिण्ड, जब विस्थापित करके मुक्त किया जाता है, 0.65 के आवर्तकाल से दोलन करता है। पिण्ड का भार कितना है?
View Solution1200Nm 'कमानी-स्थिरांक की कोई कमानी चित्र में दर्शाए अनुसार किसी क्षैतिज मेज से जड़ी है। कमानी के मुक्त सिरे से 3kg द्रव्यमान का कोई पिण्ड जुड़ा है। इस पिण्ड को एक ओर ___ 2.0 cm दूरी तक खींच कर मुक्त किया जाता है।
(i) पिण्ड के दोलन की आवृत्ति,
(ii) पिण्ड का अधिकतम त्वरण, तथा
(iii) पिण्डकी अधिकतम चाल ज्ञात कीजिए।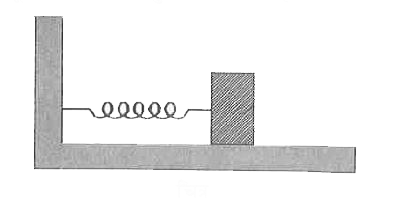
View Solutionप्रश्न 9 में,मान लीजिए जब कमानी अतानित अवस्था में है तब पिण्ड की स्थिति x=0 है तथा बाएं से दाएं की दिशा x - अक्ष की धनात्मक दिशा है। दोलन करते पिण्ड के विस्थापन x को समय के फलन के रूप में दर्शाइए, जबकि विराम घड़ी को आरंभ (t=0) करते समय पिण्ड,
(a) अपनी माध्य स्थिति, (b) अधिकतम तानित स्थिति, तथा (c) अधिकतम संपीड़न की स्थिति पर है।
सरल आवर्त गति के लिए ये फलन एक-दूसरे से आवृत्ति में, आयाम में अथवा आरंभिक कला में किस रूप में भिन्न हैं?
View Solutionचित्र में दिए गए दो आरेख दो वर्तल गतियों के तदनुरूपी हैं। प्रत्येक आरेख पर वृत्त की त्रिज्या, परिक्रमण-काल, आरंभिक स्थिति और परिक्रमण की दिशा दर्शायी गई है। प्रत्येक प्रकरण में, परिक्रमण करते कण के त्रिज्य-सदिश के x अक्ष पर प्रक्षेप के तदनुरूपी सरल आवर्त गति ज्ञात कीजिए।
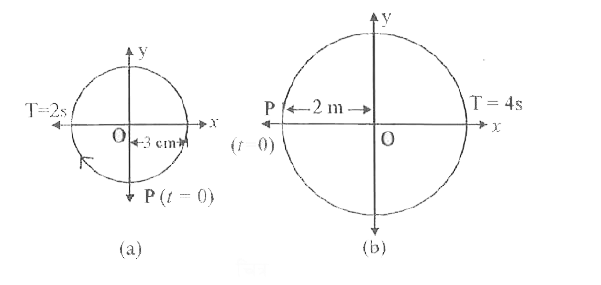
View Solutionनीचे दी गई प्रत्येक सरल आवर्त गति के लिए तदनरूपी निर्देश वृत्त का आरेख खींचिए। घूर्णी कण की आरंभिक (t =0) स्थिति, वृत्त की त्रिज्या तथा कोणीय चाल दर्शाइए। सुगमता के लिए प्रत्येक प्रकरण में परिक्रमण की दिशा वामावर्त लीजिए। (x को cm में तथा को में लीजिए।)
(a)x=-2sin (3t+`pi//3`)
(b)`x=cos (pi/6 -t)`
(c)`x=3sin (2pit+pi//4)`
(d) `x=2cos pit`
View Solutionचित्र (a) में k बल-स्थिरांक की किसी कमानी के एक सिरे को किसी दृढ़ आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के मुक्त सिरे पर बल F आरोपित करने से कमानी तन जाती है। चित्र (b) में उस कमानी के दोनों मुक्त सिरों से द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के दोनों सिरों को चित्र (b) में समान बल Fद्वारा तानित किया गया है।
(a) दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या होगा?
(b) यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन काआवर्तकाल ज्ञात कीजिए।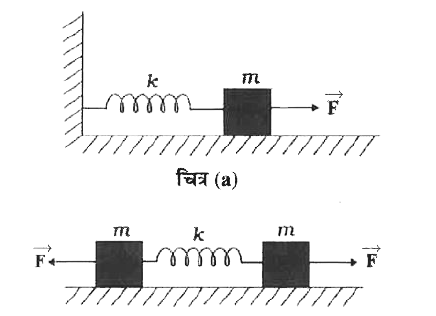
View Solutionकिसी रेलगाड़ी के इंजन के सिलिंडर हैड में पिस्टन का स्ट्रोक (आयाम का दो गुना) 1.0m का है। यदि पिस्टन 200 rad/min की कोणीय आवृत्ति से सरल आवर्त गति करता है, तो उसकी अधिकतम चाल कितनी होगी?
View Solutionचन्द्रमा के पृष्ठ पर गुरुत्वीय त्वरण 1.7ms है। यदि किसी सरल लोलक का पृथ्वी के पृष्ठ पर आवर्तकाल 3.5s है, तो उसका चन्द्रमा के पृष्ठ पर आवर्तकाल कितना होगा? (पृथ्वी के पृष्ठ पर `g = 9.8 ms^(-2)`)
View Solutionनीचे दिए गए प्रश्नों के उत्तर दीजिए:
(a) किसी कण की सरल आवर्त गति के आवर्तकाल का मान उस कण के द्रव्यमान तथा बल-स्थिरांक पर निर्भर करता है: `T=2pisqrt(m//k)` कोई सरल लोलक सन्निकट सरल आवर्त गति करता है। तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नहीं करता?
(b) किसी सरल लोलक की गति छोटे कण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है। बड़े कोणों के दोलनों के लिए एक अधिक गूढ़ विश्लेषण यह दर्शाता है कि Tका मान `2pisqrt` से अधिक होता है। इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिंतन कीजिए।
(c) कोई व्यक्ति कलाई घड़ी बाँधे किसी मीनार की चोटी से गिरता है। क्या मुक्त रूप से गिरते समय उसकी घड़ी यथार्थ समय बताती
(d) गुरुत्व बल के अंतर्गत मुक्त रूप से गिरते किसी केबिन में लगे सरल लोलक के दोलन की आवृत्ति क्या होती है?
View Solutionकिसी कार की छत से `l` लम्बाई का कोई सरल लोलक, जिसके लोलक का द्रव्यमान `M` है, लटकाया गया है। कार `R` त्रिज्या के वृत्तीय पथ पर एक समान चाल `v` से गतिमान है। यदि लोलक त्रिज्य दिशा में अपनी साम्यावस्था की स्थिति के इधर-उधर छोटे दोलन करता है, तो इसका आवर्तकाल क्या होगा?
View Solutionआधार क्षेत्रफल A तथा ऊँचाई के एक कॉर्क का बेलनाकार टुकड़ाp, घनत्व के किसी द्रव में तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते हैं, यह दर्शाइए कि कॉर्क ऊपर-नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल `T=2pisqrt((hrho)/(rho_(1)g))` है।
यहाँ `rho` कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए)।
View Solutionपारे से भरी किसी U नली का एक सिरा किसी चूषण पंप से जुड़ा है, तथा दूसरा सिरा वायुमंडल में खुला छोड़ दिया गया है। दोनों स्तंभों में कुछ दाबान्तर बनाए रखा जाता है। यह दर्शाइए कि जब चूषण पंप को हटा देते हैं, तब U नली में पारे का स्तंभ सरल आवर्त गति करता है।
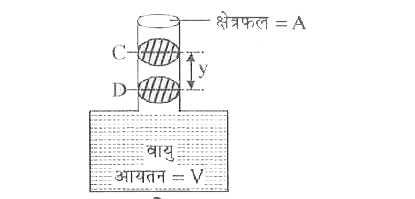
View Solutionचित्र में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ काट का क्षेत्रफल A है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है। यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते हैं, तो वह सरल आवर्त गति करती है। दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए।
View Solutionआप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं। यह मानिए कि आप इस वाहन की निलंबन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं। जब समस्त वाहन इस पर रखा जाता है, तब निलंबन 15 cm आनमित होता है। साथ ही, एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोतरी हो जाती है। निम्नलिखित के मानों का आकलन कीजिए:
(a) कमानी स्थिरांक, तथा
(b) कमानी तथा एक पहिए के प्रघात अवशोषक तंत्र के लिए अवमंदन स्थिरांक b
यह मानिए कि प्रत्येक पहिया 750 kg द्रव्यमान वहन करता है|
View Solutionयह दर्शाइए कि रैखिक सरल आवर्त गति करते किसी कण के लिए दोलन की किसी अवधि की औसत गतिज ऊर्जा उसी अवधि की औसत स्थितिज ऊर्जा के समान होती है।
View Solution10 किग्रा द्रव्यमान की कोई वृत्तीय चक्रिका अपने केंद्र से जुड़े किसी तार से लटकी है । चक्रिका को घूर्णन देकर तार में ऐंठन उत्पन्न करके मुक्त कर दिया जाता है । मरोड़ी दोलन का आवर्तकाल 1.5 सेकंड है । चक्रिका की त्रिज्या 15 सेमी है । तार का मरोड़ी कमानी नियतांक ज्ञात कीजिये । ( मरोड़ी कमानी `alpha`नियतांक सम्बद्ध `J= -alpha theta` द्वारा परिभाषित किया जाता है , यहाँ J प्र्त्यानयन बल युग्म है तथा `theta`ऐंठन कोण है )
View Solutionकोई वस्तु 5cm के आयाम तथा 0.2 सेकण्ड की आवृत्ति से सरल आवृत्ति गति करती है। वस्तु का त्वरण तथा वेग ज्ञात कीजिए जब वस्तु का विस्थापन (a) 5 cm (b) 3 cm (c) 0 cm हो।
View Solutionकिसी कमानी से लटका एक पिंड एक क्षैतिज तल में कोणीय वेग`omega` से घर्षण या अवमंदन रहित दोलन कर सकता है। इसे जब `x_(0)` दूरी तक खींचते है ओर खींचकर छोड़ देते है तो यह संतुलन केंद्र से समय t=0 पर `v_(0)`वेग से गुजरता है। प्राचल `omega, x_(0)`तथा `v_(0)` के पदों में परिणामी दोलन का आयाम ज्ञात कीजिए ( संकेत - समीकरण` x = a cos (omegat +theta)` से प्रारंभ कीजिए। ध्यान रहे की प्रारंभिक वेग ऋणात्मक है। )
View Solution
अभयास (पाठ्यपुस्तक के प्रश्न) questions and complete solutions for chapter दोलन of SANJEEV PUBLICATION of Class 11
All Exercises from SANJEEV PUBLICATION Class 11 PHYSICS दोलन
- अन्य महत्वपूर्ण प्रश्न(अतिलघूत्तरात्मक प्रश्न)
- अन्य महत्वपूर्ण प्रश्न(बहुचयनात्मक प्रश्न)
- अन्य महत्वपूर्ण प्रश्न(मिलान कीजिये)
- अन्य महत्वपूर्ण प्रश्न(रिक्त स्थानों की पूर्ति कीजिए)
- अन्य महत्वपूर्ण प्रश्न(लघूत्तरात्मक प्रश्न)
- अन्य महत्वपूर्ण प्रश्न(विस्तृत उत्तरीय प्रश्न )
- अन्य महत्वपूर्ण प्रश्न(सत्य/असत्य)
- अभयास (पाठ्यपुस्तक के प्रश्न)
- उदहारण
- गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गए प्रश्न