Complete Solutions to पाठ्यपुस्तक के उदाहरण of chapter सरल रेखाएँ of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | सरल रेखाएँ |
| SCIENCE PUBLICATION | पाठ्यपुस्तक के उदाहरण |
| Number Of Questions | 19 |
| Academic Year | 2023-24 |
उन रेखाओं के ढाल ज्ञात कीजिए जो -
(a) `(3,-2)` और `(-1,4)` बिन्दुओं से होकर जाती है।
(b) `(3,-2)` और `(7,-2)` बिन्दुओं से होकर जाती है।
(c ) `(3,-2)` और (3, 4) बिन्दुओं से होकर जाती है।
(d) धन x - अक्ष से `60^(@)` का कोण बनाती है।
View Solutionयदि दो रेखाओं के बीच का कोण `(pi)/(4)` है और रेखा की ढाल `(1)/(2)` है तो दूसरे रेखा की ढाल ज्ञात कीजिए।
View Solution`(-2,6)` और (4, 8) बिन्दुओं को मिलाने वाली रेखा (8, 12) और (x, 24) बिन्दुओं को मिलाने वाली रेखा पर लम्ब है। x का मान ज्ञात कीजिए।
View Solutionतीन बिन्दु `P(h, k), Q(x_(1),y_(1))` और `R(x_(2),y_(2))` एक रेखा पर है। दिखाइए `(h-x_(1)), (y_(2)-y_(1))=(k-y_(1))(x_(2)-x_(1))`
View Solutionनिम्न आकृति में एक रैखिक गति का समय और दूरी का लेखा चित्र दिया है। समय और दूरी को दो स्थितियाँ जब T = 0, D = 2 और जब T = 3, D = 8 अंकित की गई है। ढाल की संकल्पना का प्रयोग करके गति का नियम ज्ञात कीजिए अर्थात दूरी, समय पर किस प्रकार आश्रित है।
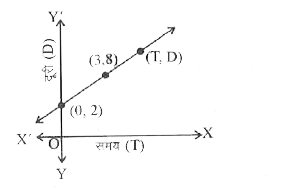
View Solutionअक्षों के समान्तर और `(-2,3)` से जाने वाली रेखाओं के समीकरण ज्ञात कीजिए।
View Solution`(-2,3)` से जाने वाली ढाल `-4` की रेखा का समीकरण ज्ञात कीजिए।
View Solutionबिन्दुओं `(1,-1)` और (3, 5) से होकर जाने वाली रेखा का समीकरण लिखिए।
View Solutionउन रेखाओं के समीकरण लिखिए जिनके लिए `tan theta = (1)/(2)` जहाँ `theta` रेखा का झुकाव है और (i) y- अंतः खण्ड `-(3)/(2)` है | (ii) x - अंतखण्ड 4 है।
View Solutionएक रेखा का समीकरण ज्ञात कीजिए जो x और y अक्ष से क्रमशः -3 और 2 के अंतः खण्ड बनाती है।
View Solutionरेखा का समीकरण ज्ञात कीजिए जिसकी मूल बिन्दु से लाम्बिक दुरी 4 इकाई और घन x - अक्ष तथा लम्ब के बीच कोण `15^(@)` है।
View Solutionफारेनहाइट ताप F और परम ताप K एक रैखिक समीकरण को सन्तुष्ट करते है। दिया है कि K = 273 जब F = 32 ओर K = 373 जब F = 212 तो K को F के पदों में व्यक्त कीजिए और F का मान ज्ञात कीजिए जबकि K = 0
View Solutionएक रेखा का समीकरण `3x-4y+10=0` है। इसके (i) ढाल (ii) x और y अन्तः खण्ड ज्ञात कीजिए।
View Solutionसमीकरण `sqrt(3x)+y-8=0` को लम्ब रूप में रूपांतरित कीजिए और P तथा `omega` के मान ज्ञात कीजिए।
View Solution`y-sqrt(3)x-5=0` और `sqrt(3)y-x+6=0` रेखाओं के बीच का कोण ज्ञात कीजिए।
View Solutionदर्शाइए कि दो रेखाएँ `a_(1)x+b_(1)y+c_(1)=0` और `a_(2)x+b_(2)y+c_(2)=0` जहाँ `b_(1), b_(2)ne 0`
(i) समान्तर है यदि `(a_(1))/(b_(1))=(a_(2))/(b_(2))` और
(ii) लम्ब है यदि `a_(1)a_(2)+b_(1)b_(2)=0`
View Solutionरेखा `x-2y+3=0` पर लम्ब और बिन्दु `(1,-2)` से जाने वाली रेखा का समीकरण ज्ञात कीजिए।
View Solutionबिन्दु `(3,-5)` की रेखा `3x-4y-26=0` से दूरी ज्ञात कीजिए।
View Solutionसमान्तर रेखाओं `3x-4y+7=0` और `3x-4y+5=0` के बीच की दूरी ज्ञात कीजिए।
View Solution
पाठ्यपुस्तक के उदाहरण questions and complete solutions for chapter सरल रेखाएँ of SCIENCE PUBLICATION MATHS (HINDI) of Class 11
All Exercises from SCIENCE PUBLICATION Class 11 MATHS सरल रेखाएँ
- अन्य महत्त्वपूर्ण उदाहरण
- पाठ्यपुस्तक के उदाहरण
- पाठ्यपुस्तक प्रश्नावली 10.1 पर आधारित अन्य महत्त्वपूर्ण प्रश्नावली
- पाठ्यपुस्तक प्रश्नावली 10.2 पर आधारित अन्य महत्त्वपूर्ण प्रश्नावली
- पाठ्यपुस्तक प्रश्नावली 10.3 पर आधारित अन्य महत्त्वपूर्ण प्रश्नावली
- पाठ्यपुस्तक विविध उदाहरण
- प्रश्नावली 10.1
- प्रश्नावली 10.2
- प्रश्नावली 10.3
- विविध प्रश्नावली 10
- विविध प्रश्नावली 10 पर आधारित महत्त्वपूर्ण प्रश्नावली