Complete Solutions to उदाहरण of chapter मात्रक एवं मापन of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | मात्रक एवं मापन |
| SCIENCE PUBLICATION | उदाहरण |
| Number Of Questions | 42 |
| Academic Year | 2023-24 |
(a) `1^(@)` (डिग्री) (b) 1' (1 आर्क मिनट) एवं (c) 1'' (1 आर्क सेकण्ड) की कोणों के मान रेडियन में परिकलित कीजिए `(360^(@) = 2pi "rad", 1^(@) = "60' एवं 1' = 60'' लीजिए")` |
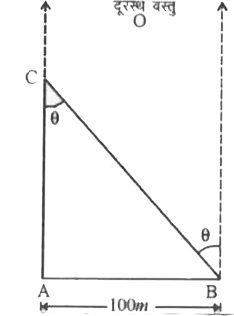
View Solutionएक व्यक्ति अपने पास की किसी मीनार की अपने से दूरी का आंकलन करना चाहता है | वह मीनार C के सामने किसी बिंदु A पर खड़ा होता है और AC की सीध में बहुत दूर स्थित किसी बिंदु O को देखता है | फिर वह AC के लंबवत 100m दूर स्थित बिंदु B तक चलता है ओर वहां से O एवं C को फिर देखता है | क्योंकि O बहुत अधिक दूरी पर है, BO एवं AO की दिशाएं व्यावहारिक रूप में एक ही हैं, लेकिन वह पाता है कि C की दृष्टि रेखा मूल दृष्टि रेखा के सापेक्ष `theta = 40^(@)` पर घूम गई है (`theta` को लंबन कहा जाता है) | उसकी मूल स्थिति A से मीनार C की दूरी का आंकलन कीजिए |
View Solutionहमारे सौर निकाय का निकटस्थ तारा (एल्फा सेंटरी) 4.29 प्रकाश वर्ष दूर है | पारसेक में यह दूरी कितनी है ? सूर्य के परित: कक्षा में 6 माह के अंतराल में दो स्थितियों से देखने पर इसका लंबन कोण कितना होगा ?
View Solutionपृथ्वी के दो व्यासत: विपरीत बिंदुओं A एवं B से चन्द्रमा का प्रेक्षण किया गया | प्रेक्षण की दो दिशाओं के बीच, चन्द्रमा पर अंतरित कोण `theta` की माप `1^(@)54'` है | पृथ्वी का व्यास लगभग `1.276 xx 10^(7) m`. है | पृथ्वी से चन्द्रमा की दूरी का अभिकलन कीजिए |
View Solutionसूर्य के कोणीय व्यास की माप 1920'' है | पृथ्वी से सूर्य की दूरी `1.496 xx 10^(11)m` है | सूर्य का व्यास परिकलित कीजिए |
View Solutionयदि किसी नाभिक का आमाप (जो वास्तव में `10^(-15) "से" 10^(-14)m` के परिसर में है) बढ़ाकर एक तीक्ष्ण पिन की नोक (`10^(-5)m "से" 10^(-14)m` के परिसर में) के बराबर कर दिया जाए, तो परमाणु का लगभग आमाप क्या है ?
View Solutionदिए गए वांडरवाल समीकरण `(P + (a)/(V^(2)))(V - b) = RT` से a तथा b की विमाएँ ज्ञात करो जहाँ a, b नियतांक है तथा P, V, R क्रमश: दाब, आयतन, तथा गैस नियतांक है |
View Solutionदिए गए संबंध में a, b की विमाएँ ज्ञात करो- `P = (b - x^(2))/(at)` जहाँ P शक्ति, x-दूरी तथा t समय |
View Solutionविमीय विधि से ऊर्जा को एक जूल से अर्ग में परवर्तित करो |
View Solutionगुरुत्वीय त्वरण (g) का मान 9.8 मीटर/सेकण्ड होता है यदि लम्बाई को किलोमीटर में तथा समय को मिनट में नापे तो g का नया मान क्या होगा ?
View Solutionपारे का घनत्व 13.6 ग्राम/सेमी। है | यदि द्रव्यमान को kg में तथा लम्बाई को मीटर में नापा जाये तो नयी पद्धति में पारे का घनत्व क्या होगा ?
View Solutionएक न्यूटन को डाइन में परिवर्तित करो |
View Solutionएक अश्व शक्ति में वॉट मात्रकों की संख्या ज्ञात करो | (1 अश्व शक्ति `= 550 xx 32` फुट पाउण्डल/से.)
View Solutionलाप्लास ने वायु में ध्वनि के वेग के लिए सूत्र `v = sqrt((gamma P)/(d))` प्राप्त किया | यहाँ v ध्वनि का वेग, P वायुमण्डलीय दाब है तथा d घनत्व तथा `gamma` एक शुद्ध अनुपात है | इस सूत्र की यथार्थता की जांच करो |
View Solutionसमीकरण `(1)/(2) mv^(2) = mgh` की विमीय दृष्टि से सत्यता की जाँच कीजिए जबकि m वस्तु का द्रव्यमान, v वेग, g गुरुत्वीय त्वरण तथा h ऊँचाई है |
View Solutionऊर्जा का SI मात्रक `J = kg m^(2) s^(-2)`, है, चाल v का `ms^(-1)` और त्वरण a का `ms^(-2)` है | गतिज ऊर्जा (K) के लिए निम्नलिखित सूत्रों में आप किस-किस को विमीय दृष्टि से गलत बताएँगे ? (m पिण्ड का द्रव्यमान है) |
(a) `K = m^(2) v^(3)`
(b) `K = (1//2) mv^(2)`
(c) K = ma
(d) `K = (3//16) mv^(2)`
(e) `K = (1//2) mv^(2) + ma`
View Solutionदो दृढ़ आधारों के बीच तनी हुई l लम्बाई वाली डोरी को कम्पन्न कराने पर उतपन्न ध्वनि की आवृति निम्न सूत्र के द्वारा दी जाती है-
`n = (1)/(2l) sqrt((Mg)/(m))`
Mg = डोरी का तनाव
m = डोरी की एकांक लम्बाई पर द्रव्यमान
तो सूत्र की सत्यता की जांच करो |
View Solutionगति के समीकरण `S = ut + (1)/(2)at^(2)` के सूत्र की सत्यता की जांच करो |
View Solutionयदि कोई m द्रव्यमान कण किसी वृताकार पथ में v वेग से घूम रहा है | यदि वृताकार पथ की त्रिज्या r हो तो अभिकेन्द्र बल `F = (mv^(2))/(r)` होगा | इस सूत्र की सत्यता की जांच करो |
View Solutionस्टोक्स ने यह ज्ञात किया कि यदि किसी पदार्थ की एक छोटी गेंद को श्याम माध्यम में गिरने दिया जाए तो उस गेंद पर माध्यम द्वारा आरोपित विस्कासिता बल F का मान निम्न बातो पर निर्भर करता हैं- (i) गेंद की त्रिज्या (r) (ii) विस्कासिता गुणांक `(eta)` (iii) गेंद का वेग v, बल के लिए सूत्र स्थापित करो |
View Solutionएक तार की कम्पनों की आवृति (n), तार की लम्बाई (l), तनाव (T) तथा प्रति एकांक लम्बाई के द्रव्यमान (m) पर निर्भर करती है | विमीय विधि से सूत्र की स्थापना करो |
View Solutionकिसी छोटी द्रव बूँद के पृष्ठ तनाव के कारण दोलन का समय T, बूँद के घनत्व d, त्रिज्या r तथा पृष्ठ तनाव S पर निर्भर करता है | विमीय विधि से सूत्र की स्थापना करो |
View Solutionएक सरल लोलक का आवर्तकाल उसके द्रव्यमान (m), लम्बाई (l) तथा गुरुत्वीय त्वरण (g) पर निर्भर करता है सूत्र की स्थापना करो |
View Solutionसूत्र `S = ut + (1)/(2) at^(2)` को विमीय विधि के द्वारा स्थापित करो | जहाँ S = दूरी, u = प्रारंभिक वेग, a = त्वरण, t = समय
View Solutionसरल आवर्त गति करते किसी पिण्ड की ऊर्जा E, पिण्ड के द्रव्यमान m, आवृति n तथा आयाम A पर निर्भर करती है | विमीय विधि से सूत्र की स्थापना करो |
View Solutionपानी का अपवर्तनांक 1.29, 1.33, 1.34, 1.35, 1.32, 1.36, 1.30 तथा 1.33 माना गया | निम्न की गणना करो-
(a) औसत मान
(b) परम त्रुटि या निरपेक्ष त्रुटि
(c) आपेक्षिक त्रुटि
(d) प्रतिशत त्रुटि
View Solutionराष्ट्रीय प्रयोगशाला में स्थित एक मानक घड़ी से तुलना करके दो घड़ियों की जाँच की जा रही है | मानक घड़ी जब दोपहर के 12 : 00 : 00 का समय दर्शाती है, तो इन दो घड़ियों के पाठ्यांक इस प्रकार हैं-
`{:(,"घड़ी 1","घड़ी 2"),("सोमवार",12 : 00 : 05,10 : 15 : 06),("मंगलवार",12 : 01 : 15,10 : 14 : 59),("बुधवार",11 : 59 : 08,10 : 15 : 18),("बृहस्पतिवार",12 : 01 : 50,10 : 15 : 07),("शुक्रवार",11 : 59 : 15,10 : 14 : 53),("शनिवार",12 : 01 : 30,10 : 15 : 24),("रविवार",12 : 01 : 19,10 : 15 : 11):}`
यदि आप कोई ऐसा प्रयोग कर रहे हो जिसके लिए आपको परिशुद्ध समय अंतराल मापन की आवश्यकता है, तो इनमें से आप किस घड़ी को वरीयता देंगे ? क्यों
View Solutionहम एक सरल लोलक का दोलन-काल ज्ञात करते हैं | प्रयोग के क्रमिक मापनों में लिए गए पाठ्यांक हैं- 2.63s, 2.56s, 2.42s, 2.71s एवं 2.80s | निरपेक्ष त्रुटि, सापेक्ष त्रुटि एवं प्रतिशत त्रुटि परिकलित कीजिए |
View Solutionएक तार के व्यास को स्क्रूगेज से नापने पर निम्न पाठ्यांक प्राप्त होते हैं- 1.328, 1.330, 1.325, 1.326, 1.334, 1.336 cm तो
(i) व्यास का माध्य (ii) माध्य परम त्रुटि (iii) प्रतिशत त्रुटि
View Solutionएक प्रयोग में दो संधारित्रों की धारिताएं `(1.3 +- 0.1) mu F` एवं `(2.4 +- 0.2)mu F` मापी गयी है | जब दोनों संधारित्र समांतर क्रम में लगे हो तो कुल धारिता ज्ञात करो एवं साथ ही प्रतिशत त्रुटि ज्ञात कीजिए |
View Solutionदो सिलेण्डरों की लम्बाई `l_(1) = (5.62 +- 0.01)` cm तथा `l_(2) = (4.34 +- 0.02)`cm लम्बाई का अंतर एवं प्रतिशत त्रुटि ज्ञात करो |
View Solutionकिसी तापमापी द्वारा मापे गए दो पिण्डो के ताप क्रमश: `t_(1) = 20^(@) C +- 0.5^(@)C` एवं `t_(2) = 50^(@) C +- 0.5^(@)C` हैं | इन पिण्डों का तापांतर और उसमें उतपन्न त्रुटि परिकलित कीजिए |
View Solutionप्रतिरोध R = V/I, जहाँ `V = (100 +- 5)V` वोल्ट एवं `I(10 +- 0.2)` एम्पियर है | R में प्रतिशत त्रुटि ज्ञात कीजिए |
View Solutionकिसी पटल की लम्बाई एवं चौड़ाई `(2.3 +- 0.2)`cm एवं `(1.6 +- 0.1)`cm. नापी गई है तो इसका क्षेत्रफल एवं त्रुटियाँ ज्ञात करो |
View Solutionयदि `Z = (A^(4)B^(1//3))/(CD^(3//2))` हो तो Z की आपेक्षिक त्रुटि ज्ञात कीजिए |
View Solutionकिसी सरल लोलक का दोलनकाल `T = 2pi sqrt(L//g)` होता है | यदि L का मापित मान 20.0 cm है जिसमें 1mm तक की यथार्थता है और समय को 1s विभेदन वाली कलाई घड़ी से मापने पर यह पाया जाता है कि लोलक के 100 दोलनों का समय 90s है तो यहाँ g के निर्धारित मान की यथार्थता क्या है ?
View Solution`R_(1) = 100 +- 3` ओम व `R_(2) = 200 +- 4` ओम के दो प्रतिरोधकों को (a) श्रेणी क्रम में, (b) पार्श्व क्रम में संयोजित किया गया है |
(a) श्रेणी क्रम संयोजन तथा (b) पार्श्व क्रम संयोजन में तुल्य प्रतिरोध ज्ञात कीजिए | (a) के लिए संबंध `R = R_(1) + R_(2)` एवं (b) के लिए `(1)/(R') = (1)/(R_(1)) + (1)/(R_(2))` तथा `(Delta R')/(R'^(2)) = (Delta R_(1))/(R_(1)^(2)) + (Delta R_(2))/(R_(2)^(2))` का उपयोग कीजिए |
View Solutionएक वस्तु `(4.0 +- 0.3)`से. में `(13.8 +- 0.2)` मी. की दूरी तय करती है त्रुटि के साथ वेग की गणना करो |
View Solutionनिम्नलिखित के लिए सार्थक अंक लिखो-
(i) 5238 N (ii) 4200 Kg. (iii) 34.000 m. (iv) 0.02340 N/m,
View Solutionकिसी घन की प्रत्येक भुजा की माप 7.203 m है | उचित सार्थक अंकों तक घन का कुल पृष्ठ क्षेत्रफल एवं आयतन ज्ञात कीजिए |
View Solutionनिम्न को सही सार्थक अंको तक हल कीजिए-
(i) `(4.0 xx 10^(-4)) - (2.5 xx 10^(-6))`
(ii) `(2.51 xx 10^(-4) xx 1.81 xx 10^(7))/(0.4463)`
(iii) 6.2 ग्राम + 4.33 ग्राम + 17.456 ग्राम
(iv) `943 xx 0.00345`
View Solutionकिसी पदार्थ के 5.74 g का आयतन 1.2 `cm^(3)` है | सार्थक अंकों को ध्यान में रखते हुए इसका घनत्व व्यक्त कीजिए |
View Solution
उदाहरण questions and complete solutions for chapter मात्रक एवं मापन of SCIENCE PHYSICS (HINDI) of Class 11