Complete Solutions to वस्तुनिष्ठ प्रश्न of chapter कार्य, शक्ति एवं ऊर्जा of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | कार्य, शक्ति एवं ऊर्जा |
| SHIVLAAL PUBLICATION | वस्तुनिष्ठ प्रश्न |
| Number Of Questions | 83 |
| Academic Year | 2023-24 |
m द्रव्यमान का एक पिण्ड नियत वेग 3u से चलता हुआ द्रव्यमान m के एक स्थिर पिण्ड से टकराता है | दोनों पिण्ड आपस में जुड़ जाते हैं संयुक्त पिण्ड का वेग क्या होगा ?
View Solutionकिसी कण पर बल `(4hati+3hatj)` न्यूटन लगाने पर वह बिंदु `(-2hati+5hatj)` मीटर से `(4hatj+3hatk)` मीटर तक विस्थापित हो जाता हैं | इस प्रक्रिया में बल द्वारा किया गया कार्य होगा :
View Solutionलम्बाई l की रस्सी के एक सिरे पर द्रव्यमान m का कण बाँधकर इसे दूसरे सिरे के सापेक्ष क्षैतिज वृत्त में चाल v से घुमाया जाता हैं | अर्द्धवृत्त घुमाने में किया गया कार्य होगा :
View Solutionएक व्यक्ति भार को पहले ऊपर तथा फिर नीचे लाता हैं | यदि उसके द्वारा कार्य केवल भार को ऊपर ले जाने में किया जाता हैं जिसके लिए ऊर्जा `3.8xx10^(7)` जूल प्रति/किग्राभार उसे शरीर की वसा से प्राप्त होती है जिसका केवल `20 %` भाग यांत्रिक ऊर्जा में बदलता हैं तो 10 किग्रा भार को 1000 बार/मीटर का ऊँचाई तक ऊपर ले जाने व नीचे लाने में व्यय वसा का द्रव्यमान होगा :
View Solution1 किग्रा द्रव्यमान का एक कण, समय पर निर्भर बल F = 6t का अनुभव करता हैं | यदि कण विरामावस्था से चलता हैं तो पहले 1 सेकण्ड में बल द्वारा किया गया कार्य होगा :
View Solution1 ग्राम द्रव्यमान की वर्षा के जल की एक बूँद, 1 किमी ऊँचाई से गिरती है और भू - तल से 50 मी/से की चाल से टकराती है | यदि 'g' का मान `"10 मी/से"^(2)` स्थिर रहे तो, ( i ) गुरुत्वीय बल तथा ( ii ) वायु के प्रतिरोधक बल द्वारा किया गया कार्य होगा :
View Solutionजब किसी स्प्रिंग को दूरी l तक ताना जाता हैं तो इसकी स्थितिज ऊर्जा 10 जूल हैं | इसको और आगे दूरी l तक तानने के लिए आवश्यक ऊर्जा होगी :
View Solutionजब रबर के एक छल्ले को दूरी x तक खींचा जाता हैं, तब परिमाण `F=ax+bx^(2)` का एक प्रत्यानयन बल लगता हैं , जहाँ a एवं b नियतांक हैं | बिना खिंचे रबर के छल्ले को l तक खींचने में किया गया कार्य हैं :
View Solutionलम्बाई 50 सेमी वाली एक भारहीन स्प्रिंग से द्रव्यमान 1.0 किग्रा का पिण्ड लटकाने पर उसकी लम्बाई में वृद्धि 2 सेमी होती हैं | पिण्ड को नीचे खींचकर स्प्रिंग की लम्बाई 60 सेमी कर दी जाती हैं | यदि `"g = 10 मीटर/सेकण्ड"^(2)` तो इस दशा में स्प्रिंग में संचित प्रत्यास्थ ऊर्जा होगी :
View Solutionकिसी स्प्रिंग का बल नियतांक K हैं | उसकी लम्बाई में `l_(1)` से `l_(2)` तक की वृद्धि करने में किया गया कार्य होगा :
View Solutionदो स्प्रिंगों जिनके बल नियतांक क्रमशः 1500 न्यूटन/मीटर तथा 3000 न्यूटन/मीटर हैं , को समान बल से खींचा जाता हैं | उनकी स्थितिज ऊर्जा का अनुपात होगा :
View Solutionदो स्प्रिंगों `S_(1)` व `S_(2)` को, जिनके बल नियतांक क्रमश : `K_(1)` व `K_(2)` हैं, समान बल से खींचने पर स्प्रिंग `S_(1)` पर स्प्रिंग `S_(2)` की अपेक्षा अधिक कार्य करना पड़ता हैं |
कथन 1 : यदि समान लम्बाई तक खींचा जाये तो `S_(1)` की अपेक्षा `S_(2)` पर अधिक कार्य करना होगा |
कथन 2 :: `K_(1) lt K_(2)`
View Solutionस्प्रिंग नियतांक K की स्प्रिंग से जुड़ा द्रव्यमान m का एक गुटका चिकनी क्षैतिज मेज पर दोलन कर रहा हैं | स्प्रिंग का दूसरा सिरा दीवार से जुड़ा हैं | स्प्रिंग की सामान्य लम्बाई पर गुटके की चाल v हैं | विराम में आने से पूर्व यदि गुटका साम्य स्थिति से दूरी x तक चलता हैं, तो :
View Solutionद्रव्यमान 0.1 किग्रा का एक पिण्ड वेग 10 मीटर/सेकण्ड से बल नियतांक 1000 न्यूटन/मीटर वाली एक स्प्रिंग से टकराता हैं ( स्प्रिंग का दूसरा सिरा कसा हैं ) तथा स्प्रिंग को सम्पीड़ित करने के पश्चात विराम पर आ जाता हैं | स्प्रिंग का सम्पीडन होगा :
View Solutionदो स्प्रिंगों के बल नियतांक क्रमश : `K_(1)` तथा `K_(2)` हैं | इन्हें इतना खींचा जाता हैं कि दोनों की स्थितिज ऊर्जाएँ समान हो जाएँ | इन पर लगाए गये बलों `F_(1)` तथा `F_(2)` का अनुपात होगा :
View Solutionसमान गतिज ऊर्जा के साथ गति कर रहे एक ट्रक और एक कार को समान मंदन बल लगाकर स्थिर अवस्था में लाया जाता है ,तब : (
View Solutionजब द्रव्यमान 1.0 किग्रा की वस्तु पर बल लगाकर उसे चलाया जाता हैं, तो उसकी स्थिति, समय के साथ निम्न प्रकार से - बदलती हैं : `x=(1)/(3)t^(3)`, जहाँ x मीटर में तथा t सेकण्ड में हैं | बल द्वारा पहले 2 सेकण्ड में किया गया कार्य होगा :
View Solutionकिसी वस्तु पर कार्यरत बल इसके द्वारा चली दूरी के व्युत्क्रमानुपाती हैं | किया गया कार्य W, विस्थापन x के साथ बदलेगा :
View Solutionएक द्रव्यमान रहित डोरी से द्रव्यमान M किग्रा का पिण्ड लटका हैं | पिण्ड को ऊर्ध्वाधर से कोण `45^(@)` तक विस्थापित करने के लिए आवश्यक क्षैतिज बल होगा :
View Solutionएक झुके हुए घर्षण रहित तल, जिसकी लम्बाई 5 मीटर तथा झुकाव कोण `theta=sin^(-1)(0.6)` हैं, पर द्रव्यमान 10 किग्रा की वस्तु को ऊपर ले जाने में किया गया कार्य होगा `("g = 10 मी/से"^(2)`) :
View Solutionएक पिण्ड जिसका द्रव्यमान 60 किलोग्राम हैं, को क्षैतिज धरातल पर रस्सी द्वारा 2 मीटर खींचा जाता हैं | यदि रस्सी का धरातल के साथ कोण `= 60^(@)` और `"g = 9 . 8 मी/से"^(2)` हैं, तो किया गया कार्य हैं :
View Solution2 किग्रा द्रव्यमान के एक ब्लॉक को नत तल पर खींचकर 10 मीटर ऊँचाई तक ऊपर ले जाने में 300 जूल कार्य करना पड़ता हैं | यदि `"g = 9 . 8 मी/से"^(2)` हैं, तो घर्षण के विरुद्ध किया गया कार्य हैं :
View Solutionद्रव्यमान m की एक कार संवेग p से गति कर रही हैं | यदि कार के टायरों एवं सड़क के मध्य घर्षण नियतांक `mu` हैं तो केवल घर्षण के कारण कार द्वारा रुकने से पूर्व तय की गई दूरी होगी :
View Solution2 किग्रा द्रव्यमान का एक ब्लॉक 4 मी/से की चाल से क्षैतिज फर्श पर गतिमान हैं | यह बिना दबी एक स्प्रिंग से टकराता हैं तथा इसे तब तक दबाता हैं जब तक कि स्वयं विराम में न आ जाए | यदि गतिक घर्षण बल 15 न्यूटन तथा स्प्रिंग नियतांक 10000 न्यूटन/मीटर हैं तो स्प्रिंग दबेगी :
View Solutionयदि किसी वस्तु पर बल f लगाने से उस वस्तु का वेग v हो जाता हैं , तो व्यय शक्ति होगी :
View Solutionओलम्पिक खेल में एक खिलाड़ी 100 मीटर दूरी 10 सेकण्ड में तय करता हैं | उसकी गतिज ऊर्जा निम्न परास में होगी :
View Solutionदो पिण्डों A तथा B के द्रव्यमान क्रमशः 1 किग्रा तथा 4 किग्रा हैं, लेकिन उनकी गतिज ऊर्जाएँ समान हैं | उनके रैखिक संवेग का अनपात होगा :
View Solutionचित्र 7.48 में दर्शाए अनुसार ऊँचाई 1 से घर्षणरहित पथ के अनुदिश विराम अवस्था से सरकने वाला कोई पिण्ड, व्यास AD = D के ऊर्ध्वाधर वृत्त को ठीक - ठीक पूरा करता हैं | तब ऊँचाई h होगी :

View Solutionसमय t = 0 पर एक कण X - अक्ष पर गति प्रारम्भ करता हैं | यदि उसकी गतिज ऊर्जा, समय t के साथ एकसमान रूप से बढ़ रही है तो उस पर आरोपित बल अनुक्रमानुपाती होगा :
View Solutionm = 10 - 2 किग्रा द्रव्यमान का एक पिण्ड एक माध्यम में जा रहा हैं और एक घर्षण बल `F=-kv^(2)` का अनुभव करता हैं | पिण्ड का प्रारम्भिक वेग `v_(0)=10` मी/से हैं | यदि 10 सेकण्ड के बाद उसकी ऊर्जा `(1)/(8)mv_(0)^(2)` हैं हो k का मान होगा :
View Solutionसरल रेखा में गति करते पिण्ड का संवेग यदि `20 %` बढ़ जाता हैं, तो उसकी गतिज ऊर्जा में प्रतिशत वृद्धि होगी :
View Solutionयदि किसी पिण्ड का संवेग `100 %` बढ़ जाता हैं तो इसकी गतिज ऊर्जा बढ़ेगी:
View Solutionयदि किसी पिण्ड की गतिज ऊर्जा में `0.1 %` की वृद्धि होती हैं, तो उसके संवेग में प्रतिशत वृद्धि होगी :
View Solutionएक किलोवाट - घंटा बराबर हैं :
View Solutionबन्दूक से एक गोली छोड़ी जाती है | फलस्वरूप बन्दूक प्रतिक्षिप्त हो जाती है | बन्दूक का द्रव्यमान, गोली के द्रव्यमान का 100 गुना है | गोली तथा बन्दूक की गतिज ऊर्जाओं का अनुपात होगा :
View Solutionएक गेंद जिसकी गतिज ऊर्जा E है, क्षैतिज से कोण `45^(@)` पर फेंकी गयी है | इसकी उड़ान के दौरान उच्चतम बिंदु पर गतिज ऊर्जा होगी :
View Solution100 ग्राम द्रव्यमान के एक कण को 5 मी/से की चाल से ऊर्ध्वाधर ऊपर की ओर फेंका जाता है | ऊपर जाने के दौरान गुरुत्व बल द्वारा किया गया कुल कार्य होगा :
View Solutionद्रव्यमान m की एक वस्तु त्रिज्या R वाले अर्द्धगोलीय प्याले के धरातल पर इसके किनारे से नीचे की ओर सरकती है | प्याले की तली पर पहुँचने पर वस्तु का वेग होगा :
View Solutionकिसी गतिशील पिंड का वेग दोगुना कर देने पर दोगुना हो जाता है :
View Solutionएक पिंड को हाथ से छोड़ने के उपरांत तथा इसके पृथ्वी तल से टकराने से पूर्व अपरिवर्तित रहने वाली राशि है :
View Solutionवेग V से चलता हुआ द्रव्यमान m का एक गोला एक रेत के लटके बोरे में घुसकर रुक जाता है | यदि बोरे का द्रव्यमान M है और वह ऊँचाई h ऊपर उठता है, तो गोले का वेग था :
View Solutionलम्बाई l तथा द्रव्यमान m की एक पतली एकसमान छड़ अपने एक सिरे से गुजरती क्षैतिज अक्ष के परितः स्वतंत्रतापूर्वक दोलन कर रही है | इसकी अधिकतम कोणीय चाल `omega` है | इसके द्रव्यमान केंद्र द्वारा उठी अधिकतम ऊँचाई होगी :
View Solutionअपनी निम्नतम स्थिति पर एक लोलक के गोलक की चाल 3 मी/से है | लोलक की लम्बाई 0.5 मीटर है | जब यह लम्बाई ऊर्ध्वाधर से कोण `60^(@)` बनाती है, तो गोलक की चाल होगी `(g = 10" मी/से"^(2))` :
View Solutionहाथ द्वारा एक बल लगाकर ऊर्ध्वाधरतः ऊपर की ओर एक 0.2 किग्रा द्रव्यमान की गेंद को फेंका जाता है | यदि बल लगाते समय हाथ 0.2 मीटर गति करता है तथा तत्पश्चात गेंद 2 मीटर गति करती है तो `g = 10" मी/से"^(2)` मानने पर गेंद पर हाथ द्वारा लगाया गया बल होगा :
View Solutionअचर शक्ति देने वाली एक मशीन द्वारा एक पिंड को विरामावस्था से सीधी रेखा में चलाते हैं | समय t में पिंड द्वारा चली गयी दूरी अनुक्रमानुपाती होगी :
View Solutionएक पतली छड़ ( लम्बाई l, द्रव्यमान m ) का एक सिरा जमीन पर है | इसे ऊर्ध्वाधर रखकर इस प्रकार गिरने दिया जाता है कि जमीन वाला सिरा फिसलता नहीं है | जमीन से टकराते समय दूसरे सिरे का वेग होगा :
View Solutionकिसी व्यक्ति का ह्रदय, धमनियों से 150 मिमी पारे के दाब पर, 5 लीटर रक्त प्रति मिनट पम्प करता है | यदि पारे का घनत्व `13.6xx10^(3)" किग्रा/मी"^(3)" तथा "g = 10" मी/से"^(2)` है तो, ह्रदय की शक्ति है :
View Solutionकिसी टरबाईन की ब्लेडों ( पंखों ) पर 100 किग्रा/सेकण्ड की दर से झरने से पानी गिर रहा है | यदि झरने की ऊँचाई 100 मीटर है तो टरबाईन को दी गयी शक्ति होगी :
View Solutionद्रव्यमान m की एक कार त्वरण a से सीधी समतल सड़क पर एक नियत प्रतिरोधी बल R के विरुद्ध चलायी जाती है | जब कार का वेग v है, तो इंजन द्वारा कार पर कार्य करने की दर होगी :
View Solutionदो बल `F_(1)` और `F_(2)` के कारण M द्रव्यमान का एक पिंड एक घर्षण रहित तल पर 10 मीटर/सेकण्ड की समान चाल से चल रहा है | समायोजन की कुल शक्ति है :
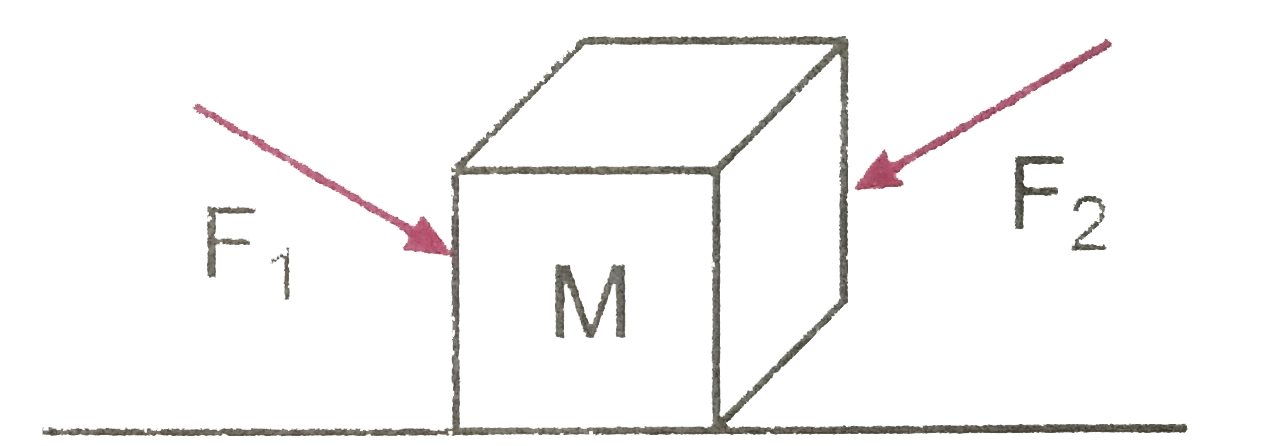
View Solutionद्रव्यमान m का एक बिंदु कण एक खुरदरे पथ PQR पर चल रहा है | ( चित्र 7.50 ) | कण तथा पथ के बीच घर्षण गुणांक `mu` को P से छोड़ने पर वह rR पर पहुँच कर रुक जाता है | पथ के भाग PQ तथा QR में व्यय ऊर्जा समान है | यदि पथ PQ से QR पर जाने में कोई ऊर्जा व्यय नहीं होती है तो `mu` तथा दूरी QR = x के मान हैं क्रमशः
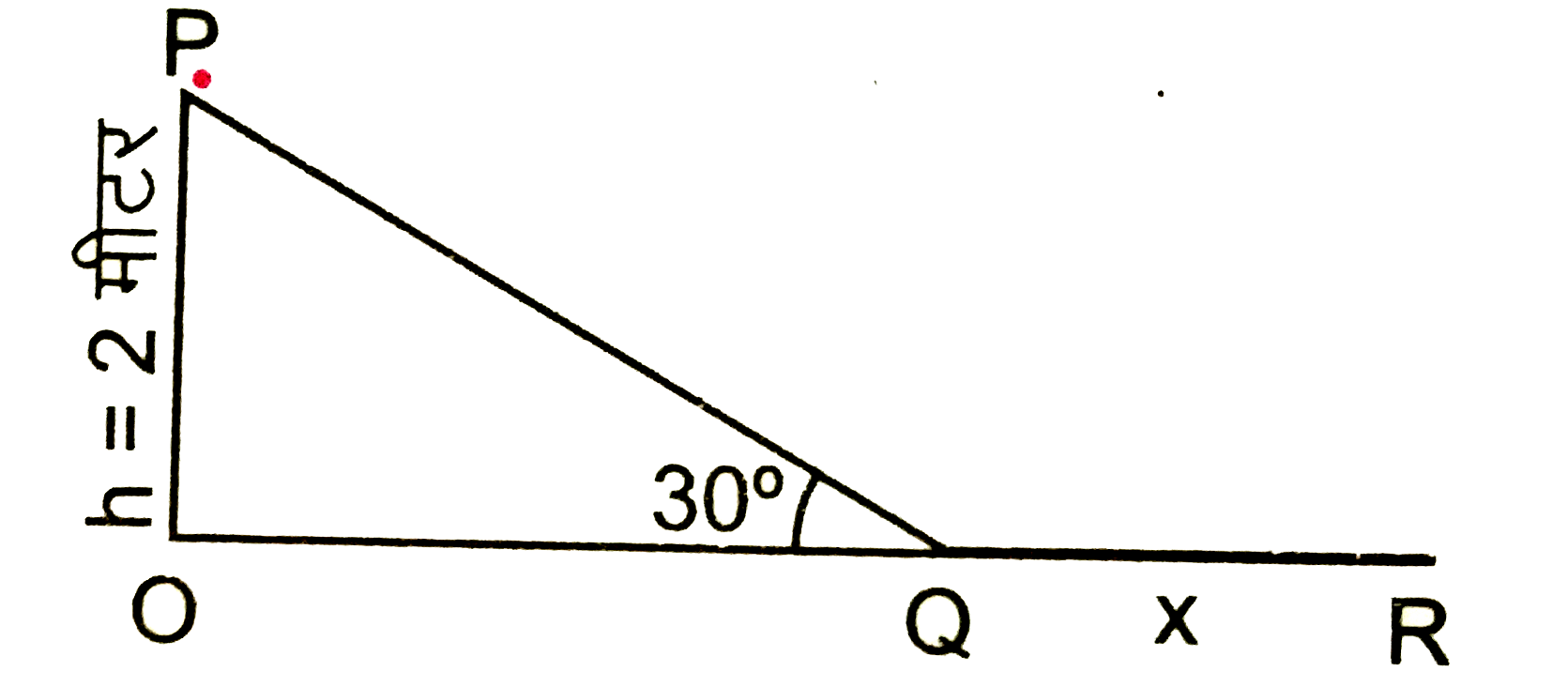
View Solutionसत्य कथन है :
View Solutionदो पिंडों की प्रत्यास्थ टक्कर में संरक्षित रहता है :
View Solutionएक गेंद फर्श पर टकराती है तथा अप्रत्यास्थ टक्कर के बाद उछलती है | इस दशा में :
View Solutionसंघट्ट में स्थिर राशियाँ हैं :
View Solutionदो कणों की प्रत्यास्थ टक्कर में संरक्षित रहता है :
View Solutionद्रव्यमान m का एक कण वेग `vecv` से चलते हुए एक उसी द्रव्यमान के स्थिर कण से सीधी टक्कर करता है | टक्कर के पश्चात पहले कण का वेग होगा :
View Solutionद्रव्यमान m की एक गेंद वेग v से चलकर, वेग 2v से सामने से आती हुई समान द्रव्यमान की दूसरी गेंद से सम्मुख प्रत्यास्थ टक्कर करती है | वेग v की दिशा को धनात्मक मानते हुए, टक्कर के बाद गेंदों के वेग होंगे :
View Solutionक्षैतिज वेग 400 मी/से से चलती हुई द्रव्यमान 10 ग्राम की एक गोली, द्रव्यमान 2 किग्रा के लकड़ी के एक गुटके से टकराती है | गुटका एक हल्की अवितान्य तथा लम्बाई 5 मीटर वाली डोरी से लटका है | यदि गोली के टकराने से गुटके का गुरुत्व केंद्र ऊर्धाधार ऊपर 10 सेमी उठ जाता है तो गुटके से क्षैतिज दिशा में बाहर निकलने पर गोली की चाल होगी :
View Solutionविरामावस्था में यूरेनियम के एक नाभिक का क्षय थोरियम तथा हीलियम के नाभिकों में होता है, तो :
View Solutionएक गेंद 8 सेमी ऊँचाई से गिरायी जाती है | यदि गेंद का फर्श से संघट्ट पूर्ण प्रत्यास्थ है, तो वह पुनः ऊपर उछलेगी :
View Solutionएक पिंड का द्रव्यमान m तथा प्रारम्भिक वेग v है | दूसरे पिण्ड जो कि स्थिर रखा है तथा जिसका द्रव्यमान M है, से सम्मुख टक्कर करता है | यदि टक्कर के पश्चात द्रव्यमान m वाला पिण्ड स्थिर हो जाए और केवल द्रव्यमान M वाला पिण्ड गति करे, तो यह तभी होगा, जबकि :
View Solution6 मी/से की क्षैतिज चाल से चलता हुआ एक द्रव्यमान m का कण उसी दिशा में 4 मी/से की चाल से चल रहे द्रव्यमान M के एक भारी कण से टक्कर करता है | यदि `mltltM`है तो टक्कर के बाद हल्के कण की चाल होगी, जबकि टक्कर पूर्ण प्रत्यास्थ हो :
View Solution050 ग्राम द्रव्यमान की एक गोली 10 मी/से के वेग से 950 ग्राम के एक स्थिर गुटके से टकराकर उसी में फँसी रह जाती है | गतिज ऊर्जा में हानि होगी :
View Solutionएक 20 किग्रा द्रव्यमान की एक वस्तु जो 10 मीटर/सेकण्ड की चाल से चल रहा है, एक 5 किग्रा के स्थिर द्रव्यमान से टकराता है | टकराने पर दोनों द्रव्यमान चिपक जाते हैं | संयुक्त द्रव्यमान की गतिज ऊर्जा होगी :
View Solutionद्रव्यमान 4m वाला एक कण स्थिर अवस्था में फटकार तीन भागों में विभाजित होता है | द्रव्यमान m वाले दो कण चाल v से एक - दूसरे से लम्बवत दिशा में जाते हैं | इस प्रक्रिया में मुक्त ऊर्जा होगी :
View Solutionविस्फोट में एक पिण्ड आसमान द्रव्यमान के दो पिण्डों में टूट जाता है | इस घटना में :
View Solutionद्रव्यमान m का एक पिण्ड वेग u से चलता हुआ द्रव्यमान 3m के दूसरे स्थिर पिण्ड से प्रत्यास्थातः टकराता है | टक्कर के बाद दूसरे पिण्ड का वेग होगा :
View Solutionद्रव्यमान m का एक कण वेग v से चलता हुआ एक स्थिर द्रव्यमान 2m के एक अन्य कण से टकराता है तथा उससे चिपक - जाता है | निकाय की चाल होगी :
View Solutionद्रव्यमान m का एक गतिशील गुटका, 4m द्रव्यमान के किसी दूसरे स्थिर गुटके से संघट्ट करता है | संघट्ट के पश्चात हल्का गुटका विराम अवस्था में आ जाता है | यदि हल्के गुटके का आरंभिक वेग v है, तो प्रत्यानयन गुणांक (e) का मान होगा :
View Solutionएक एकरेखीय संघट्ट में, आरंभिक चाल `v_(0)` वो का एक कण समान द्रव्यमान के एक दूसरे रुके हुए कण से टकराता है | यदि कुल अंतिम गतिज ऊर्जा, आरंभिक गतिज ऊर्जा से `50 %` ज्यादा हो तो टक्कर के बाद दोनों कणों के सापेक्ष गति का परिमाण होगा :
View Solutionकथन : द्रव्यमान m का एक बिंदु कण चाल v से चलकर द्रव्यमान M एक स्थिर बिंदु कण से टकराता है | यदि अधिकतम ऊर्जा हानि `fxx(1)/(2)mv^(2)` हो तो `f=(m)/(m+M)` होगा |
कथन 2 : अधिकतम ऊर्जा की हानि तब होती है जबकि टकराने के उपरांत दोनों कण आपस में मिल जाते है |
View Solutionयदि एक न्यूट्रॉन की एक स्थिर अवस्था के ड्यूटीरियम से प्रत्यास्थ एक रेखीय संघट्ट होती है तो उसकी ऊर्जा का आंशिक क्षय `P_(d)` पाया जाता है | उसके स्थिर अवस्था के कार्बन नाभिक से समरूप संघट्ट में ऊर्जा का आंशिक क्षय `P_(c)` पाया जाता है | `P_(d)` तथा `P_(c)` के मान क्रमश : होगें :
View Solutionएक न्यूट्रॉन वेग v से गति करता हुआ, एक द्रव्यमान A संख्या के परमाणु से सीधी एवं प्रत्यास्थ टक्कर करता है | यदि न्यूट्रॉन की प्रारम्भिक गतिज ऊर्जा E है, तो टक्कर के पश्चात न्यूट्रॉन की गतिज ऊर्जा होगी :
View Solution0 . 50 किग्रा द्रव्यमान का एक गुटका किसी घर्षण रहित ( चिकने ) पृष्ठ पर 2.00 मी/से की चाल से गतिशील है | यह 1.00 किग्रा द्रव्यमान के किसी अन्य पिण्ड से टकराता है तथा फिर दोनों एक साथ एकल पिण्ड के रूप में गति करते हैं | संघट्ट में हुई ऊर्जा की हानि है :
View SolutionX - दिशा में चाल 2v से चलते हुए द्रव्यमान m के एक कण से, Y - दिशा में वेग v वेग से चलता हुआ द्रव्यमान 2m का एक कण टकराता है | यदि यह संघट्ट ( टक्कर ) पूर्णतः अप्रत्यास्थ है तो, टक्कर के दौरान ऊर्जा का क्षय ( हानि ) होगी :
View Solutionचाल v से पूर्व की ओर चलते हुए द्रव्यमान m का एक कण, समान द्रव्यमान तथा समान चाल v से uttar की ओर चलते हुए एक - दूसरे कण से टकरा जाता है , तथा दोनों कण संलयित हो जाते हैं | द्रव्यमान 2m के नए कण की चाल होगी :
View Solution5 किग्रा द्रव्यमान का एक पिण्ड 10 किग्रा मीटर/सेकण्ड के संवेग से गतिशील है | 0.2 न्यूटन का बल पिण्ड पर उसकी गति की दिशा में 10 सेकण्ड तक लगाया जाता है | पिण्ड की गतिज ऊर्जा में वृद्धि होगी :
View Solutionतोप से एक गोला क्षैतिज से कोण `theta` बनाते हुए वेग v मीटर/सेकण्ड से छोड़ा जाता है | अपने पथ के उच्चतम बिंदु पर उसमें विस्फोट होकर वह समान द्रव्यमान के दो टुकड़ों में फट जाता है | इनमें से एक टुकड़ा अपना पथ दोहराते हुए तोप पर वापस जा पहुँचता है | विस्फोट के तुरंत बाद दूसरे टुकड़े की चाल मी/से में होगी :
View Solutionद्रव्यमान 4m का एक पिण्ड X - Y समतल पर विरामावस्था में है | यह अचानक तीन टुकड़ों में विस्फोटित होता है | दो टुकड़े ( प्रत्येक द्रव्यमान m ) एक - दूसरे के लम्बवत समान चाल v से चलते हैं | विस्फोट में उत्पन्न कुल गतिज ऊर्जा होगी :
View Solutionप्रकाश विद्युत् प्रभाव उदाहरण है :
View Solutionकथन 1 : एक दिशा में गतिमान दो कण पूर्ण अप्रत्यास्थ टक्कर में सम्पूर्ण ऊर्जा नहीं खोते हैं |
कथन 2 : सभी संघट्टों में संवेग संरक्षण का नियम लागू होता है |
View Solutionकिसी घर्षणहीन पृष्ठ पर चाल v से चलता हुआ द्रव्यमान M का एक ब्लॉक, उसी द्रव्यमान m के विरामावस्था में स्थित एक अन्य ब्लॉक से टकराता है | टक्कर के पश्चात पहला ब्लॉक, चाल `(v)/(3)` से, अपनी प्रारम्भिक गति की दिशा से कोण `theta` पर चलने लगता है| टक्कर के पश्चात दूसरे ब्लॉक की चाल होगी :
View Solution
वस्तुनिष्ठ प्रश्न questions and complete solutions for chapter कार्य, शक्ति एवं ऊर्जा of SHIVALAL AGARWAL AND CO PHYSICS (HINDI) of Class 11
All Exercises from SHIVLAAL PUBLICATION Class 11 PHYSICS कार्य, शक्ति एवं ऊर्जा
- NCERT पाठ्य पुस्तक के प्रश्नोत्तर
- अति लघु उत्तरीय प्रश्न
- आंकिक उदाहरण
- आंकिक प्रश्न
- तथ्यात्मक प्रश्न
- निबन्धात्मक प्रश्न
- प्रश्न (उचित जोड़ियाँ बनाइए - )
- प्रश्न (एक शब्द/वाक्य में उत्तर दीजिए -)
- प्रश्न (बताइए कि निम्न कथन सत्य हैं अथवा असत्य-)
- प्रश्न (रिक्त स्थान की पूर्ति कीजिए - )
- प्रश्न (वस्तुनिष्ठ प्रश्न )
- बोधात्मक प्रश्न
- लघु उत्तरीय प्रश्न
- वस्तुनिष्ठ प्रश्न
- संख्यात्मक प्रश्न