Complete Solutions to Example of chapter Mechanical Properties of Solids of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | Mechanical Properties of Solids |
| SL ARORA | Example |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
The length of a suspended loire increases by `10^-4` of its original length when a stress of `10^7 Nm^-2` is applied on it. Calculate the Young's modulus of the material of the wire.
View SolutionA uniform wire of steel of length 2.5m and density `8.0gcm^(-3)` weighs 50g. When stretched by a force of `10kgf` , the length increases by 2mm. Calculate Young's modulus of steel.
View SolutionA structural steel rod has a radius of 10 mm and a length of 1.0 m. A 100 kN force stretches it along its length. Calculate (a) stress, (b) elongation, and ( c ) strain on the rod. Young's modulus, of structural steel is 2.0 `xx` `10^(11)` N `"m"^(-2)`.
View SolutionA structural steel rod has a radius of 10 mm and a length of 1.0 m. A 100 kN force stretches it along its length. Calculate (a) stress, (b) elongation, and ( c ) strain on the rod. Young's modulus, of structural steel is 2.0 `xx` `10^(11)` N `"m"^(-2)`.
View SolutionA structural steel rod has a radius of 10 mm and a length of 1.0 m. A 100 kN force stretches it along its length. Calculate (a) stress, (b) elongation, and ( c ) strain on the rod. Young's modulus, of structural steel is 2.0 `xx` `10^(11)` N `"m"^(-2)`.
View SolutionWhat is the percentage increase in length of a wire of diameter 2.5 mm, stretched by a force of 100 kg wt ? Young's modulus of elasticity of wire `=12.5xx10^(11) dyn e//cm^(2)`.
View SolutionThe breaking stress for a metal is `7.8 xx 10^9 Nm^-2`. Calculate the maximum length of the wire of this metal which may be suspended breaking. The density of the metal =`7.8 xx 10^3kg m^-3`. Take g =`10 N kg^-1`
View SolutionA rubber string 10m long is suspended from a rigid support at its one end. Calculate the extension in the string due to its own weight. The density of rubber is `1.5xx10^(3)` and Young's modulus for the rubber is `5xx10^(6)Nm^(-2)` Take `g=10Nkg^(-1)` .
View SolutionA silica glass rod has a diameter of1cmand is 10 cmlong. The ultimate strength of glass is `50 x 10^6 Nm^-2`. Estimate the largest mass that can be hung from it without breaking it. Take `g =10 N kg^-1`.
View SolutionA composite wire of uniform diameter 3.0 mm consisting of a copper wire of length 2.2m and a steel wire of length 1.6m stretches under a load by 0.7 mm. Calculate the load, given that the Young's modulus for copper is `1.1 xx 10^(11) Pa` and for steel is `2.0 xx 10^(11)Pa`.
View SolutionThe maximum stress that can be applied to the material of a wire used to suspend an elevator is `(3)/(pi)xx10^(8)N//m^(2)` if the mass of elevator is 900 kg and it move up with an acceleration `2.2m//s^(2)` than calculate the minimum radius of the wire.
View SolutionA mass of 100 grams is attached to the end of a rubber string 49 cm. long and having an area of cross section 20 sq. mm. The string is whirled round, horizontally at a constant speed of 40 r.p.s in a circle of radius 51 cm. Find Young's modulus of rubber.
View SolutionA uniform heavy rod of weight W, cross sectional area a and length L is hanging from fixed support. Young modulus of the material of the rod is Y. Neglect the lateral contraction. Find the elongation of the rod.
View SolutionA steel wire of uniform cross-section `1 mm^(2)` is heated to `70^(@)C` and stretched by tying it two ends rigidly. Calculate the change in tension on the wire when temperature falls form `70^(@)C` to `35^(@)C`
View SolutionThe presssure of a medium is changed from `1.01xx10^(5) Pa` to ` 1.165xx10^(5) Pa` and change in volume is `10 % ` keeping temperature constant . The bulk modulus of the medium is
(a) `204.8 xx 10^(5) Pa` (b) `102.4xx10^(5) Pa` (c ) `5.12xx10^(5) Pa`
(d) `1.55xx10^(5) Pa`
View SolutionThe average depth of indian Ocean is about 3000 m. The fractional compression, `(triangleV)/(V)` of water at the bottom of the ocean is (Given Bulk modulus of the water `=2.2xx10^9Nm^-2` and `g=10ms^-2`)
View SolutionA sphere contracts in volume by `0.01%` when taken to the bottom of sea `1km` keep. The bulk modulus of the material of the sphere is (Given density of sea water may be taken as `1.0xx10^3kgm^-3`).
View SolutionIf the normal density of sea water is `1.00 g//cm^(3)`, what will be its density at a depth of 4km? Given compressibility of water = 0.00005 per atmosphere. 1 atmospheric pressure `=10^(6) dyn e//cm^(2), g=980 cm//s^(2)`.
View SolutionA cube is subjected to pressure of `5 xx 10^(5)N//m^(2)`. Each side of the cube is shortened by 1%. Find volumetric strain and bulk modulus of elasticity of cube.
View SolutionCalculate the presure required to stop the increases in volume of a copper block when it is heated from `50^(@)` to `70^(@)C` . Coefficient of linear expansion of copper `=8.0xx10^(-6).^(@)C^(-1)` and bulk modulus of elasticity `3.6xx10^(11)Nm^(-2)`
View SolutionA cube of aluminimum of each side 4 cn is subjected to a tangential (shearing) force. The top face of the cube is sheared through `0.012` cm with respect to the bottom face. Find (i)shearing strain (ii) shearing stress and shearing force. Given `eta=2.08xx10^(11)` dyne `cm^(2)`
View SolutionA cube of aluminimum of each side 4 cn is subjected to a tangential (shearing) force. The top face of the cube is sheared through `0.012` cm with respect to the bottom face. Find (i)shearing strain (ii) shearing stress and shearing force. Given `eta=2.08xx10^(11)` dyne `cm^(2)`
View SolutionA square lead slab of side 50 cm and thickness 10.0 cm is subjected to a shearing force (on its narrow face) of magnitude `9.0xx10^(4)N`. The lower edge is riveted to the floor. How much is the upper edge displaced, if the shear modulus of lead is `5.6xx10^(9)` Pa?
View SolutionA rubber block `1cmxx3cm10cm` is clamped at one end with its 10cm side vertical. A horizontal force of 30 N is applied to the free surface. What is the horizontal displacement of the top face ? Modulus of rigidity of rubber `1.4xx10^(5)Nm^(-2)`
View SolutionA 60 kg motor rests on four cylinderical rubber blocks. Each cylinder has a height of 3cm and a cross-sectional area of `15cm^(2)` . The shear modulus for this rubber is `2xx10^(6)Nm^(-2)` . If a sideways force of 300N is applied to the motor, how far will it move sideways?
View SolutionA steel wire of 4.0 m is stretched through 2.0 mm. The cross - sectional area of the wire is `2.0 mm^2.` If young's modulus of steel is `2.0 xx10^(11) Nm^(-2)` find (i) the energy density of the wire, (ii) the elastic potential energy stored in the wire.
View SolutionA steel wire of 4.0 m is stretched through 2.0 mm. The cross - sectional area of the wire is `2.0 mm^2.` If young's modulus of steel is `2.0 xx10^(11) Nm^(-2)` find (i) the energy density of the wire, (ii) the elastic potential energy stored in the wire.
View SolutionCalculate the increase in energy of a brass bar of length 0.4 m and cross-sectional area `1 cm^(2)`,when compressed with a load of 4kg wt along its length.Given Young's Modulus of Elasticity is `Y=1.0 xx 10^(11)Nm^(-2)`
View SolutionWhen the load on a wire is slowly increased from `3kgwt` to `5 kg wt`, the elongation increases from `0.61` to `1.02 mm`. The work done during the extension of wire is
View SolutionA 40 kg boy whose leg are `4cm^2` in area and `50cm` long falls through a height of `2m` without breaking his leg bones. If the bones can stand a stress of `1.0xx10^8(N)/(m^2)`, calculate the Young's modulus for the material of the bone.
View SolutionDefine Poisson's ratio.Write an expression for it. What is the significance of negative sign in this expression ?
View SolutionDetermine the Poisson's ratio of the material of a wire whose volume remains constant under an external normal stress.
View SolutionOne end of a nylon rope of length 4.5 m and diameter 6 mmis fixed to a tree limb. A monkey weighing 100 N jumps to catch the free end and stays there. Find the elongation of the rope and the corresponding change in the diameter. Young modulus of nylon =0.2.
View SolutionA material has Poisson's ratio `0.5`, If a uniform rod of it suffers a longtiudinal strain of `2xx10^(-3)` then the percentage increases in its volume is
View SolutionA material has Poisson's ratio 0.2. If a uniform rod of it suffers longitudinal strain 4.0 `xx` `10^-3` calculate the percentage change in its volume
View SolutionIntermolecular Forces
View SolutionIn solids interatomic forces are
View SolutionIntermolecular Forces
View SolutionState the factors due to which three states of matter differ from each other.
View SolutionCrystalline solids are called true solids.Why ?
View SolutionWhat is a perfectly elastic body ? Give an example.
View SolutionStatement I: Young's modulus for a perfectly plastic body is zero.
Statement II: For a perfectly plastic body, restoring force is zero.
View SolutionNo material is perfectly elastic. Why ?
View SolutionCan one distinguish between the internal energy of a body acquired by het transfer and that acquired by the performance of work on it by an etenal agent ?
View SolutionWhat are the factors on which the modulus of elesticity depends?
View SolutionA constant voltage is applied between the two ends of a metallic wire. If both the length and the radius of the wire are doubled, the rate of heat developed in the wire
View SolutionStress and pressure are both force per unit area. How do you differentiate between them?
View SolutionOut of solids , liquids and gases, which one has all the three types of modulus ofelasticity and why gases have only bulk modulus of elasticity.
View SolutionWhich type of elasticity is involved in the following cases ? Compressing of gas
View SolutionWhich type of elasticity is involved in the following cases ? Compressing a liquid
View SolutionWhich type of elasticity is involved in the following cases ? Stretching a wire
View SolutionWhich type of elasticity is involved in the following cases ? Tangential push on the upper face of a block
View SolutionWhat does the slope of stress vs strain graph indicate?
View SolutionHow does Young's modulus change with rise in temperature?
View SolutionGlass, rubber, steel copper is order of increasing the property of elasticity
View SolutionWhat is more elastic : water or air, why?
View SolutionWhy is a spring made of steel, not of copper?
View SolutionWhen we stretch a wire, we have to perform work. Why? What happens to the energy given to the wire in this process?
View SolutionWhat happens to the work done instreching a wire?
View SolutionIdentical spring of steel and copper are equally stretched. On which, more work will have to be done ?
View SolutionThere are two idential springs of copper and steel. They are stretched by equal forces. For which spring more work will have to be done?
View SolutionA wire gets heated when it is bent back and forth. Why?
View SolutionA hard wire is broken by bending repeatedly in alternating directions. Why ?
View SolutionExplain why should the beams used in the construction of bridge and small breadth.
(ii) Why are girders given I shape?
View SolutionThe ratio stress/strain remains constant for small deformation. What will be the effect on this ratio when the deformation made is very large?
View SolutionThe young's modulus of a wire of length (L) and radius (r ) is Y. If the length is reduced to` L/2` and radius `r/2` , then its young's modulus will be
View SolutionA wire fixed at the upper end stretches by length l by applying a force F. The work done in stretching is
View SolutionA wire suspended vertically from one of the its ends is stretched by attaching a weight of 200 N to the lower end. The weight stretches the wire by 1 mm. then the elastic energy stored in the wire is
View SolutionIf 'S' is stress and 'Y' is young's modulus of material of a wire, the energy stored in the wire per unit volume is
View SolutionA wire stretches by a certain amount under a load. If the load and radius are increased to four times, find the stretch caused in the wire.
View SolutionWhich one is more elastic rubber or steel? Explain.
View SolutionTwo different types of rubber are found to have the stress-strain curves as shown. Thenbr>
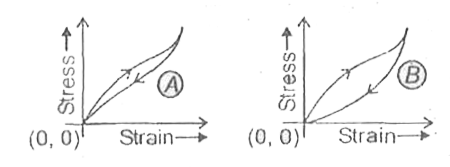
View SolutionRead each of the statement below carefully and state, with reasons, if it is true or false.
(a) The modulus of elasticity of rubber is greater than that of steel.
(b) the stretching of a coil is determined by its shear modulus.
View SolutionTwo wires of the same length and material but different radii `r_(1)` and `r_(2)` are suspended from a rigid support both carry the same load at the lower end. The ratio of the stress devedoped in the second wire to that developed in the first wire is
View SolutionWill the stress and strain in all wires be the same?
View SolutionA cable is replaced by another cable of the same length and material but of double the diameter.
(i) Under a given load which cable will show greater extension?
(ii) How many times the second cable can support the maximum load without exceeding the elastic limit?
View SolutionTwo wires of same length and material but of different radii are suspended from a rigid support. Both carry the same load. Will the stress, strain and extension in them be same or different ?
View SolutionA uniform plant of Young's modulus Y is moved over a smooth horizontal surface by a constant horizontal force F. The area of cross section of the plank is A. The compressive strain on the plank in the direction of the force is
View SolutionWhat are the factors which affect the elasticity of a material ?
View SolutionWhat is the role of physics in your daily life?
View SolutionWhy a spring balance does not give correct measurements when it has been used for a long time?
View SolutionWhy are the bridge declared unsafe after long use?
View SolutionTwo idential solid balls, one of ivory and the other of wet caly, are dropped from the same height on the floor. Which one will rise to a greater height after striking the floor and why ?
View SolutionIf F is the breaking force of a wire, what will be the breaking force for (a) two parallel wires of the same size (b) for a single wire of double the thickness?
View SolutionGraphite consists of planes of carbon atoms. Between atoms in the planes there are only weak forces. What kind of elastic properties do you expect from graphite ?
View SolutionWhy does modulus of elasticity of most of the materials decrease with the increase of temperature?
View SolutionA wire elongates by l mm when a load W is hanged from it. If the wire goes over a pulley and two weights W each are hung at the two ends, the elongation of the wire will be (in mm)
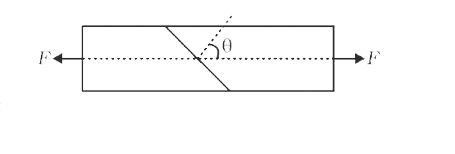
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle `theta` with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of `theta` is the tensile stress maximum
(iv) For what value of `theta` is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle `theta` with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of `theta` is the tensile stress maximum
(iv) For what value of `theta` is the shearing stress maximum?

View SolutionA bar of cross section `A` is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle `theta` with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of `theta` is the tensile stress maximum?
d. For what value of `theta` is the shearing stress maximum?
View SolutionA bar of cross section `A` is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle `theta` with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of `theta` is the tensile stress maximum?
d. For what value of `theta` is the shearing stress maximum?
View SolutionA metallic wire is stretched by suspending weight to it. If `alpha` is the longitudinal strain and Y its Young's modulus of elasticity, shown that the elastic potential energy per unit volume is given by `Y alpha^(2)//2`
View SolutionA copper wire of negligible mass, `1 m` length and cross-sectional area `10^(-6) m^(2)` is kept on a smooth horizontal table with one end fixed. A ball of mass `1 kg` is attached to the other end. The wire and the ball are rotating with an angular velocity of `20 rad//s`. If the elongation in the wire is `10^(-3) m`.
a. Find the Young's modulus of the wire (in terms of `xx 10^(11) N//m^(2)`).
b. If for the same wire as stated above, the angular velocity is increased to `100 rad//s` and the wire breaks down, find the breaking stress (in terms of `xx 10^(10) N//m^(2)`).
View SolutionA load of 31.4 kg is suspended from a wire of radius `10^(-3)` m and density `9xx10^3 kg//m^3` Calculate the change is temperature of the wire if 75% of the work done is converted into heat. The Young's modulus and the specific heat capactiy of the meterial of the wire are `9.8 xx 10^(10) N//m^2 and 490 J//kg//K` respectively.
View SolutionAlight rod of length 2 m is suspended horizontlly from the ceiling bty means of two vertical wirs of equal length tied to its ends One wire is mode of steel and is of cross - section 0.1 sq cm and the other is of brass of cross -section 0.2 sq cm Find the postion along the rod at which a wight may be hung to produce (i) equal stress in both wirs (ii) equal strain in both wires (Y for brass `=10xx10^(10) Nm^(-2) and Y "for steel" =20xx10^(10) Nm^(-2)`)
View SolutionA thin rod of negligible mass and area of cross-section `4 xx 10^(-6)m^(2)`, suspended vertically from one end has a length of `0.5 m` at `10^(@)C`. The rod is cooled art `0^(@)C`, but prevented from contracting by attaching a mass at the loose end. Find
`(i)` This mass and
`(ii)` The energy stored in the rod.
Given for this rod, `Y = 10^(11)Nm^(-2)`, coefficient of linear expansion `= 10^(-5)K^(-1)` and `g = 10ms^(-2)`.
View SolutionA stone of 0.5 kg mass is attached to one end of a `0.8` m long aluminium wire of `0.7` mm diameter and suspended vertically . The stone is now rotated in a horizontal plane at a rate such that the wire makes an angle of `85^(@)` with the vertical . find the increase in the length of the wire . The Young's modulus of aluminium = `7 xx 10^(10) Nm^(-2) , sin 85^(@) = 0.9962 , cos 85^(@) = 0.0872`
View SolutionA steel wire of length 4.87 mm and cross-section `3.0 xx 10^(-5) m^(2)` stretches by the same amout as a copper wire of length 3.5 m and cross -section `4.0 xx 10^(-5) m^(2)` under a given load . White is the ratio of the Young's modulus of steel so that of copper ?
View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is `2.0 xx 10^(11)`Pa and that of brass is `9.1 xx 10^(11)` Pa.
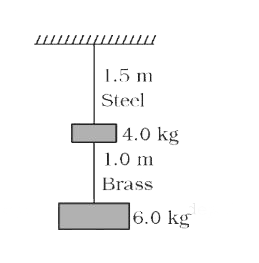
View SolutionThe edges of an aluminum cube are `10 cm` long. One face of the cube is firmly fixed to a vertical wall. A mass of `100 kg` is then attached to the opposite face of the cube. Shear modulus of aluminum is `25 xx 10^(9) Pa`, the vertical deflection in the face to which mass is attached is
View Solution
Example questions and complete solutions for chapter Mechanical Properties of Solids of DHANPAT RAI & CO PHYSICS (HINGLISH) of Class 11