Complete Solutions to Example of chapter Kinetic Theory of gases of Class 11 book with complete answers and questions

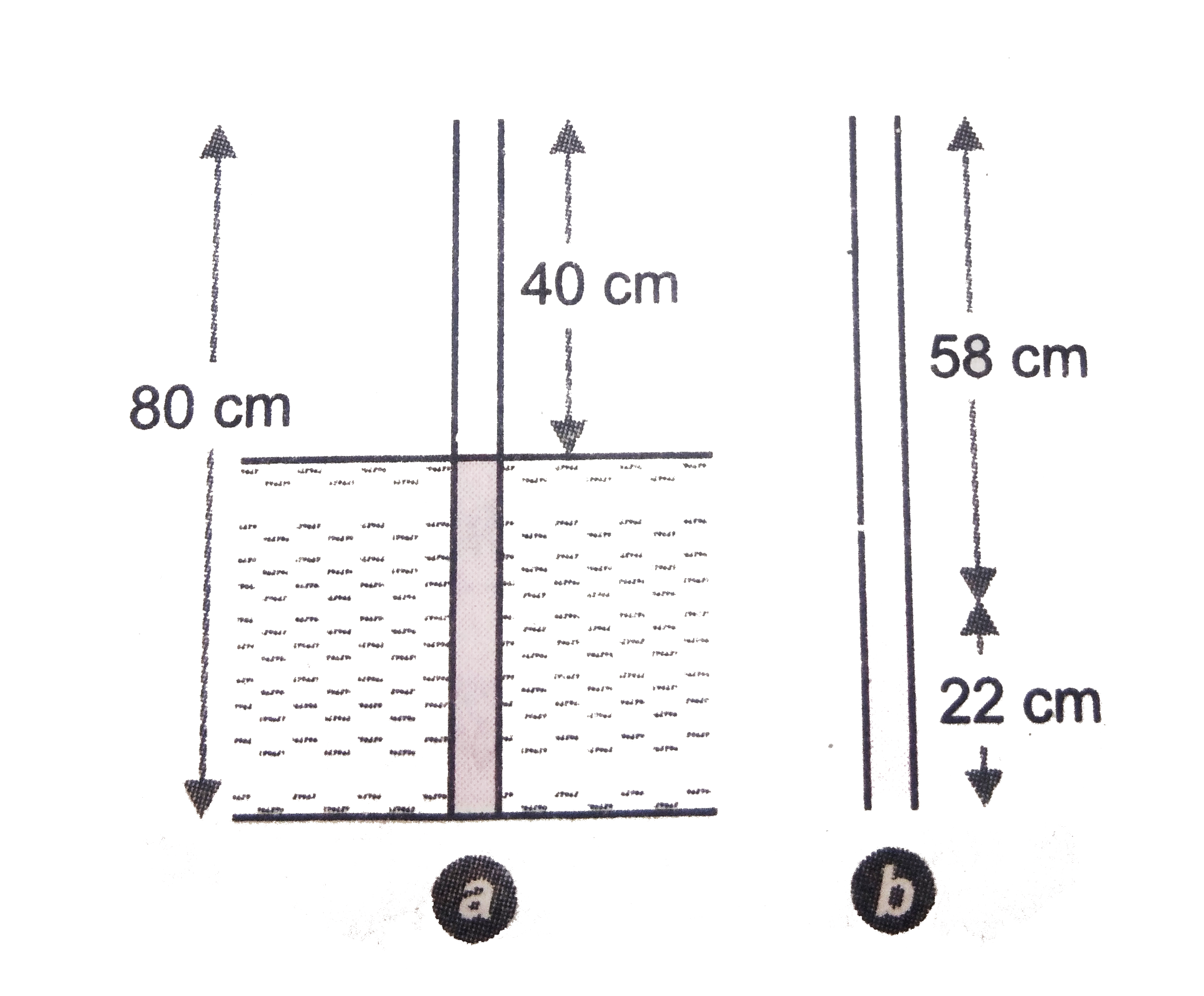
A narrow uniform glass tube 80 cm long and open at both ends is half immersed in mercurry. Then the top of the tube is closed and it is taken out of mercury. A column of mercury 22 cm long then remains in the tube. What is the atmospheric pressure?

A gas at `27^@ C` in a cylinder has a volume of 4 litre and pressure `100 Nm^-2`.
(i) Gas is first compressed at constant temperature so that the pressure is `150 Nm^-2` . Calculate the change in volume.
(ii) It is then heated at constant volume so that temperature becomes `127^@ C`. Calculate the new pressure.

A gas at `27^@ C` in a cylinder has a volume of 4 litre and pressure `100 Nm^-2`.
(i) Gas is first compressed at constant temperature so that the pressure is `150 Nm^-2` . Calculate the change in volume.
(ii) It is then heated at constant volume so that temperature becomes `127^@ C`. Calculate the new pressure.

As an air bubble rises from the bottom of a lake to the surface, its volume is doubled. Find the depth of the lake. Take atmospheric pressure = 76 cm of Hg.

Using the ideal gas equation, determine the value of gas constant R. Given that one gram mole of a gas at S.T.P occupies a volume of 22.4 litres

A balloon partially filled with helium has a volume of `30 m^3`, at the earth's surface, where pressure is `76 cm` of (Hg) and temperature is `27^@ C` What will be the increase in volume of gas if balloon rises to a height, where pressure is `7.6 cm` of `Hg` and temperature is `-54^@ C` ?

A vessel contains two non-reactive gases neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of
(i) number of molecules, and
(ii) mass density of neon and oxygen in the vessel.
Atomic mass of neon = 20.2 u, and molecular mass of oxygen = 32.0 u.

A vessel contains two non-reactive gases neon (monoatomic) and oxygen (diatomic). The ratio of their partial pressures is 3:2. Estimate the ratio of
(i) number of molecules, and
(ii) mass density of neon and oxygen in the vessel.
Atomic mass of neon = 20.2 u, and molecular mass of oxygen = 32.0 u.

A closed container of volume `0.02m^(3)` contains a mixture of neon and argon gases at a temperature `27^(@)C` and pressure `1 xx 10^(5) Nm ^(-1)` The total mass is 28 and the molar mass of and argon are `20` and `40` respectively find the masses of individual gases in the container assuming then to be ideal .

Calculate the r.m.s. velocity of air molecules at `S.T.P.` Given density of air at `S.T.P.` is `1.296 kg m^(-3)`.

A vessel is filled with a gas at a pressure of 76 cm of mercury at a certain temperature. The mass of the gas is increased by 50% by introducing more gas in the vessel at the same temperature. Find the resultant pressure of the gas.

Calculate the kinetic energy of one mole of argon at `127^(@)C`. Given,Boltzmann's constant, `k_(B) = 1.381 xx 10^(-23) J "molecular"^(-1) K^(-1)`. Avogardro numbe, `N = 6.02 xx 10^(23) "mol"^(-1)`

Calculate the KE per molecule and also rms velocity of a gas at `127^(@)C`. Given `k = 1.38 xx 10^(-23) J "molecule"^(-1) K^(-1)` and mass of each molecule `= 6.4 xx 10^(-27) kg`.

Calculate the number of molecule in `2 xx 10^(-6)m^(3)` of a perfect gas at `27^(@) C` and at a pressure of 0.01 m of mercury. Mean KE of a molecule at `27^(@) C = 4xx10^(-11) J and g = 9.8 m//s^(2)`.

Calculate the root mean square speed of one gram molecule of hydrogen at S.T.P. Given that the density of hydrogen at S.T.P. Is 0.09kg `m^-3` and R =8.31 J `mole^-1` `K^-1`.

(a) Calculate (i) root-mean-square speed and (ii) the mean energy of 1 mol of hyderogen at STP given that density of hydrogen is `0.09 kg//m^(3)`. (b) Given that the mass of a molecule of hydergen is `3.34 xx 10^(-27)` kg, calculate Avogadro's number. (c ) Calculate Boltmann's constant.

Calculate Boltzmann's constent.

At what temperature will the average velocity of oxygen molecules be sufficient so as to escape from the earth ? Escape velocity of earth is `11.0 kms^(-1)` and mass of one molecule of oxygen is `5.34xx10^(-26)` kg. Boltzmann constant `=1.38xx10^(-23) " J molecule"^(-1) K^(-1)` .

A vessel A contains hydrogen and another vessel B whose volume is twice that of A contains same mass of oxygen at same temperature. Compare
(i) average KE of hydrogen and oxygen molecule.
(ii) root mean square speeds of molecules
(iii) pressure of gases in A and B.
Molecular weight of hydrogen and oxygen are 2 and 32 respectively.

A vessel A contains hydrogen and another vessel B whose volume is twice that of A contains same mass of oxygen at same temperature. Compare
(i) average KE of hydrogen and oxygen molecule.
(ii) root mean square speeds of molecules
(iii) pressure of gases in A and B.
Molecular weight of hydrogen and oxygen are 2 and 32 respectively.

A vessel A contains hydrogen and another vessel B whose volume is twice that of A contains same mass of oxygen at same temperature. Compare
(i) average KE of hydrogen and oxygen molecule.
(ii) root mean square speeds of molecules
(iii) pressure of gases in A and B.
Molecular weight of hydrogen and oxygen are 2 and 32 respectively.

A flask contains argon and chlorine in the ratio 2:1 by mass. The temperature of the mixture is `27^(@)C`. Obtain the ratio of
`(i)` average kinetic energy per molecule, and
`(ii)` root mean square speed of the molecules of two gases.
Atomic mass of argon = 39.9 u, Molecular mass of chlorine = 70.9 u.

A flask contains argon and chlorine in the ratio 2:1 by mass. The temperature of the mixture is `27^(@)C`. Obtain the ratio of
`(i)` average kinetic energy per molecule, and
`(ii)` root mean square speed of the molecules of two gases.
Atomic mass of argon = 39.9 u, Molecular mass of chlorine = 70.9 u.

Two perfect monoatomic gases at absolute temperature `T_(1)` and `T_(2)` are mixed. There is no loss of energy. Find the temperature of the mixture if the number of moles in the gases are` n_(1)` and `n_(2)`.

Four molecules of a gas have speeds `2, 4, 6` and `8 kms^(-1)` respectively. Calculate their average speed and root mean square speed.

If three gas molecules have velocity `0.5`, `1` and `2 km//s` respectively, find the ratio of their root mean square speed and average speed.

Calculate the r.m.s. velocity of oxygen molecule at S.T.P. The molcular weight of oxygen is 32.

The rms velocity of hydrogen at S.T.P is `u` `ms^(-1)`. If the gas is heated at constant pressure till its volume is three fold, what will be its final temperature and rms velocity ?

The rms speed of oxygen molecules at a certain temperature is `upsilon`. If the temperature is doubled and the oxygen gas dissociates into atomic oxygen, the rms speed would be

At what temperature is the r.m.s velocity of a hydrogen molecule equal to that of an oxygen molecule at `24^@C`?

Calculate the temperature at which r.m.s velocity of gas molecules is double its value at `27^(@)C`, pressure of the gas remaining the same.

Calculate the temperature at which rms velocity of a gas is half it's value at `0^@C` , pressure remaining constant

Uranium has two isotopes of masses 235 and 238 units. If both are present in uranium hexa fluoride gas, which would have the larger average speed ? If atomic mass of fluorine is 19 units, estimate the percentage difference in speed at any temperature.

The total number of degrees of freedom possessed by the molecules in `1cm^(3)` of `H_(2)` gas at temperature 273 K and 1 atm pressure . Will be

Calculate the internal energy of 1 gram of oxygen at NTP.

Hydrogen is heated in a vessel to a temperature of 10,000K. Let each molecule posses an average energy `E_(1)`. A few molecules escape into the atmosphere at 300 K. Due to collisions, their energy changes to `E_(2)`. Calculate ratio `E_(1)//E_(2)`.

The molecular kinetic energy of 1 g of helium (molecular weight 4) at `127^(@)C` is (Given , R `=8.31 J"mol"^(-1)K^(-1)` )

How many degrees of freedom are associated with `2` gram of helium at NTP ? Calculate the amount of heat energy required to raise the temp. Of this amount from `27^(@) C to 127^(@) C`. Given Boltzmann constant `k_(B) = 1.38 xx 10^(-23)` erg `"molecule"^(-1) K^(-1)` and Avogadro's number `=6.02 xx 10^(23)`.

Calculate the limiting ratio of the internal energy possessed by helium and hydrogen gases at 10,000K.

A cylinder of fixed capacity 44.8 litres contains helium gas at standard pressure at temperature . What is the amount of heat need to rest that temperature of the gas by `15.00^@C ? [ R = 8.31 " J mol"^(-1)K^(-1)]`

One mole of a monoatomic gas is mixed with three moles of a diatomic gas. What is the molecular specific heat of mixture at constant volume? `R=8.31 J mol^(-1) K^(-1)`.

One mole of ideal monoatomic gas `(gamma=5//3)` is mixed with one mole of diatomic gas `(gamma=7//5)`. What is `gamma` for the mixture? `gamma` Denotes the ratio of specific heat at constant pressure, to that at constant volume

A gaseous mixture consists of 16g of helium and 16 g of oxygen. The ratio `(C_p)/(C_v)` of the mixture is

A gaseous mixture enclosed in a vessel consists of one gram mole of a gas A with `gamma=(5/3)` and some amount of gas B with `gamma=7/5` at a temperature T.
The gases A and B do not react with each other and are assumed to be ideal. Find the number of gram moles of the gas B if `gamma` for the gaseous mixture is `(19/13)`.

The density of water is `1000 kg m^(-3)`. The density of water vapour at `100^(@) C` and 1 atmospheric pressure is `0.6 kg m^(-3)`. The volume of a molecule multiplied by the total number gives what is called, molecular volume. Estimate the ratio (or fraction) of the molecular volume to the total volume occupied by the water vapour under the above conditions of temperature and pressure.

The volume of water molecule is
Take, density of wter is `10^(3) kg m^(-3)` and avogadros' number `=610^(23) "mole"^(-1))`

What is the average distance between atoms (interatomic distance) in water ?