Complete Solutions to PART D of chapter ANNUAL EXAMINATION QUESTION PAPER MARCH 2013 NORTH of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | ANNUAL EXAMINATION QUESTION PAPER MARCH 2013 NORTH |
| SUBHASH PUBLICATION | PART D |
| Number Of Questions | 10 |
| Academic Year | 2023-24 |
Prove that `cos 6x =32 cos ^(6) x -48cos ^(4) x + 18 cos ^(2) x -1`
View Solution`1^(3)+2^(3)+3^(3)+………….+n^(3)=(n^(2)(n+1)^(2))/4 forall n in N.`
View SolutionA group consists of 7 boys and 5 girls . Find the number of ways in which a team of 5 members can be selected so as to have atleast one boy and girl.
View SolutionDerive the equation of the ellipse in the form `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`.
View SolutionProve that `Lim _( xto 0) ( sin x) /( x ) =1` ( x being measured in radians )
View SolutionFind the mean deviation about the mean for the following data.
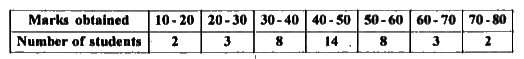
View SolutionProve geometrically that `cos (x+y) =cosx cosy +sin x sin y `
View SolutionFind the sum to n terms of the series `1^(2)+(1^(2)+2^(2))+(1^(2)+2^(2)+3^(2))+.....`
View SolutionDerive a formula for the angle between two lines with slopes `m_(1) and m_(2)`. Hence the slopes of the lines which make an angle `pi/4` with the line `x-2y+5=0`
View SolutionFind ` (dy)/(dx) ` if y=x `sin x - (x^(2) )/( 13+tan x) `
View Solution
PART D questions and complete solutions for chapter ANNUAL EXAMINATION QUESTION PAPER MARCH 2013 NORTH of JEEVITH PUBLICATIONS MATHS (KANNADA ENGLISH) of Class 11