Complete Solutions to EXERCISE of chapter கணங்கள்,தொடர்புகள் மற்றும் சார்புகள் of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | கணங்கள்,தொடர்புகள் மற்றும் சார்புகள் |
| SURA PUBLICATION(TAMIL) | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
கீழ்காண்பவைகளை பட்டியல் முறையில் எழுதுக.`{x in NN:x^2<121 மற்றும் x ஒரு பகா எண்ணாகும்} `
View Solutionகீழ்காண்பவைகளை பட்டியல் முறையில் எழுதுக `(x-1)(x+1)(x^2-1)=0`எனும் சமன்பாட்டின் மிகை மூலங்களின் கணம்
View Solutionகீழ்காண்பவைகளை பட்டியல் முறையில் எழுதுக `{x in NN:4x+9<52}`
View Solutionகீழ்காண்பவைகளை பட்டியல் முறையில் எழுதுக ` {x:}frac{x-1}{x+2}=3,x in RR-{-2}`
View Solution`{-1,1}`எனும் கணத்தை கணக் கட்டமைப்பு முறையில் எழுதுக
View Solutionகீழ்காண்பவைவற்றுள் எவை முடிவுள்ள கணம் , முடிவில்லாத கணம் என்பதனைக் குறிப்பிடுக `{x in NN:xஎன்பது ஒரு இரட்டை படை பகா எண்}`
View Solutionகீழ்காண்பவைவற்றுள் எவை முடிவுள்ள கணம் , முடிவில்லாத கணம் என்பதனைக் குறிப்பிடுக `{x in NN:xஎன்பது ஒரு ஒற்றை படை பகா எண்}`
View Solutionகீழ்காண்பவைவற்றுள் எவை முடிவுள்ள கணம் , முடிவில்லாத கணம் என்பதனைக் குறிப்பிடுக `{x in ZZ:xஎன்பது பத்தை விடக் குறைந்த இரட்டை படை எண்}`
View Solutionகீழ்காண்பவைவற்றுள் எவை முடிவுள்ள கணம் , முடிவில்லாத கணம் என்பதனைக் குறிப்பிடுக `{x in RR:xஎன்பது ஒரு விகிதமுறு எண்}`
View Solutionகீழ்காண்பவைவற்றுள் எவை முடிவுள்ள கணம் , முடிவில்லாத கணம் என்பதனைக் குறிப்பிடுக `{x in NN:xஎன்பது ஒரு விகிதமுறு எண்}`
View Solutionபின்வருவனவற்றுள், தகுந்த கணங்களைக் கொண்டுக் சரிபார்க்கவும் `Axx(BcapC)=(AxxB)cap(AxxC)`
View Solutionபின்வருவனவற்றுள், தகுந்த கணங்களைக் கொண்டுக் சரிபார்க்கவும் `Axx(BcupC)=(AxxB)cup(AxxC)`
View Solutionபின்வருவனவற்றுள், தகுந்த கணங்களைக் கொண்டுக் சரிபார்க்கவும்`(AxxB)cap(BxxA)=(AcapB)(BcapA)`
View Solutionபின்வருவனவற்றுள், தகுந்த கணங்களைக் கொண்டுக் சரிபார்க்கவும் `C-(B-A)=(CcapA)cup(CcapB)`
View Solutionபின்வருவனவற்றுள், தகுந்த கணங்களைக் கொண்டுக் சரிபார்க்கவும் `(B-A)capC=(BcapC)-A=Bcap(C-A)`
View Solutionபின்வருவனவற்றுள், தகுந்த கணங்களைக் கொண்டுக் சரிபார்க்கவும் (vi)`(B-A)cupC=(BcupC)-(A-C)`
View Solution''ஒரு கணத்திலுள்ள ஓர் உறுப்பு எப்பொழுதும் தன் கணத்திற்கே உட்கணமாக அமையாது '' என்ற கூற்றின் உண்மைத்தண்மையை ஆராய்க.
View Solutionn(P(A))=1024` n(AcupB)=15` மற்றும் `n(P(B))=32` எனில்`n(AcapB)` காண்க
View Solution`n(AcapB)=3`மற்றும்`n(AcupB)=10` எனில்,`n(P(AtriangleB)` காண்க
View Solution`AxxA`என்ற கணத்தில் 16 உறுப்புகள் உள்ளன. மேலும் அதிலுள்ள இரு உறுப்புகள்`(1,3)` மற்றும் `(0,2)`எனில் `A`உறுப்புகளைக் காண்க.
View Solution`n(A)=3`மற்றும்`n(B)=2` எனும் நிபந்தனைக்குட்பட்டு அமைந்துள்ள இரு கணங்கள்`A,B` ஆகும்`(x, 1) (y,2)(z,1)`என்பவை`AxxB` எனும் கணத்திலுள்ள சில உறுப்புகள் எனில், `A,B`கணங்களைக் காண்க(இங்கு , முற்றிலும் வேறுபட்ட உறுப்புகள் )
View Solution`AxxA`கணத்திலுள்ள`16` உறுப்புகள் உள்ளன.`S={(a,b)inAxxA:a < b}` என்ற கணத்தில் உள்ள உறுப்புகள் இரு உறுப்புகள் `(-1,2)`மற்றும்`(0,1)` எனில் `S`இல் உள்ள மீதமுள்ள உறுப்புகளை காண்க.
View Solutionகீழ்காணும் தொடர்புகளுக்கு தற்கட்டு, சமச்சீர் மற்றும் கடப்பு ஆகியவற்றை பற்றி ஆராய்க. மிகை முழு எண்களின் தொடர்பு ஆனது ன் வகுத்தி ஆக இருந்தால் என வரையறுக்கப்படுகிறது?
View Solutionகீழ்காணும் தொடர்புகளுக்கு தற்கட்டு, சமச்சீர் மற்றும் கடப்பு ஆகியவற்றை பற்றி ஆராய்க. `P`என்பது தளத்திலுள்ள அனைத்து நேர்கோடுகளின் கணத்தைக் குறிப்பதாகக் கொள்க. தொடர்பு`R` என்பது`l` ஆனது`m` க்குச் செங்குத்தாக`lRm` இருந்தால் என வரையறுக்கப்படுகிறது
View Solutionகீழ்காணும் தொடர்புகளுக்கு தற்கட்டு, சமச்சீர் மற்றும் கடப்பு ஆகியவற்றை பற்றி ஆராய்க. `A`என்பது ஒரு குடும்பத்தின் உறுப்பினர்கள் அனைவரையும் கொண்ட கணமாக கருதுக `a`என்பவர் `b`-ன் சகோதரி இல்லையெனில் தொடர்பு `R`ஆனது`aRb` என வரையறுக்கப்படுகிறது
View Solutionகீழ்காணும் தொடர்புகளுக்கு தற்கட்டு, சமச்சீர் மற்றும் கடப்பு ஆகியவற்றை பற்றி ஆராய்க.`A`என்பது ஒரு குடும்பத்தின் பெண் உறுப்பினர்கள் அனைவரையும் கொண்ட கணம் என்க. தொடர்பு`R` என்பவர்`a` என்பவர் `b` ன் சகோதரி இல்லையெனில் தொடர்பு `R`ஆனது`aRb` என வரையறுக்கப்படுகிறது
View Solutionகீழ்காணும் தொடர்புகளுக்கு தற்கட்டு, சமச்சீர் மற்றும் கடப்பு ஆகியவற்றை பற்றி ஆராய்க.அனைத்தும் இயல் எண்களின் கணத்தில் தொடர்பு`R`என்பது`x+2y=1` எனில் `xRy`என வரையறுக்கப்படுகிறது`x,y inNN`
View Solution`X={a,b,c,d}`மற்றும்`R={{a,a},{b,b},{a,c}}` என்க .தொடர்பு `R`-ஐ (i)தற்சுட்டு (ii)சமச்சீர் (iii) கடப்பு(iv) சமானத் தொடர்பு என உருவாக்க உடன் சேர்க்கப்பட வேண்டிய குறைந்தபட்ச உறுப்புகளை எழுதுக ?
View Solution`A={a,b,c}`மற்றும்`R={{a,a},{b,b},{a,c}} `R` -ஐ (i)தற்சுட்டு (ii)சமச்சீர் (iii) கடப்பு(iv) சமானத் தொடர்பு என உருவாக்க உடன் சேர்க்கப்பட வேண்டிய குறைந்தபட்ச உறுப்புகளை எழுதுக ?
View Solutionஒரு தளத்திலுள்ள அனைத்து முக்கோணங்களின் கணத்தை `P`என்போம் `P`ல் `R`என்ற தொடர்பானது `a`ஆனது`b` ன் வடிவொத்தமாக இருப்பின்`aRb` என வரையறுக்கப்படுகிறது. `R`என்பது சமானத் தொடர்பு என நிறுவுக
View Solutionஇயல் எண்களின் கணத்தில்`R` என்பது`2a+3b=30` எனில்`aRb` என வரையறுக்கப்படுகிறது.`R`ல் உள்ள உறுப்புகளை எழுதுக. அது (i)தற்சுட்டு (ii)சமச்சீர் (iii)கடப்பு (iv)சமானத் தொடர்பா என்பதை சரிபார்க்க
View Solutionசென்னையில் உள்ள மக்களின் கணத்தில் ''நட்பு'' ஒரு சமானத் தொடர்பன்று என்பதை நிரூபிக்க
View Solutionஇயல் எண்களின் கணத்தில்`R` என்பது`a+b le6` எனில்`aRb` என வரையறுக்கப்படுகிறது.`R`ல் உள்ள உறுப்புகளை எழுதுக. அது (i)தற்சுட்டு (ii)சமச்சீர் (iii)கடப்பு (iv)சமானத் தொடர்பா என்பதை சரிபார்க்க
View Solution`A={a,b,c}`என்க `A`ன் மீதான மிகச்சிறிய செவ்வெண்மையுடைய சமானத் தொடர்பு என்ன? `A`ன் மீதான மிகப்பெரிய செவ்வெண்மையுடைய சமானத் தொடர்பு என்ன ?
View Solution`ZZ`ல்`m-n` ஆனது `7`ஆல் வகுக்கபடுமெனில்`mRn` எனத் தொடர்பு `R`வரையறுக்கப்பட்டால் `R`என்பது சமானத் தொடர்பு என நிருபிக்க
View Solutionஒரு பள்ளியில் பதினோராம் வகுப்பில் `4` பிரிவுகளில் மொத்தம் `120`மாணவர்கள் படிகின்றனர். மாணவர்களின் கணம் `A`மற்றும் பிரிவுகளின் கணம் `B`என்க . `x`என்ற மாணவர் `y`பிரிவிலிருந்தால் `x`ஆனது`y` உடன் தொடர்புடையது என வரையறுக்கப்படுகிறது. இத்தொடர்பு சார்ப்பாகுமா? இதன் நேர்மாறு தொடர்பு பற்றி விளக்குக?
View Solution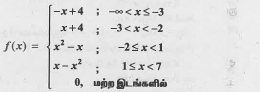 மற்ற இடங்களில் என வரையறுக்கப்படின் `-4,1,-2,7,0` ஆகியவற்றில் ன் மதிப்புக்களை காண்க
மற்ற இடங்களில் என வரையறுக்கப்படின் `-4,1,-2,7,0` ஆகியவற்றில் ன் மதிப்புக்களை காண்க
View Solution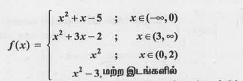 மற்ற இடங்களில் என வரையறுக்கப்படின் `-3,5,2,-1,0` ஆகியவற்றில் ன் மதிப்புக்களை காண்க
மற்ற இடங்களில் என வரையறுக்கப்படின் `-3,5,2,-1,0` ஆகியவற்றில் ன் மதிப்புக்களை காண்க
View Solutionகீழ்காணும் தொடர்புகள் சார்புகளா? என்பதனைச் சோதிக்கவும். சார்புகள் எனில் அவை ஒன்றுக்கொன்றா மற்றும் மேற்கோர்த்தலா எனச் சோதிக்கவும். சார்பு இல்லை எனில் காரணம் கூறவும் ? `A={a,b,c} f={(a,c)(b,c)(c,b),(f:A rightarrow A)`
View Solutionகீழ்காணும் தொடர்புகள் சார்புகளா? என்பதனைச் சோதிக்கவும். சார்புகள் எனில் அவை ஒன்றுக்கொன்றா மற்றும் மேற்கோர்த்தலா எனச் சோதிக்கவும். சார்பு இல்லை எனில் காரணம் கூறவும் ? `x={x,y,z}`மற்றும்`f={(x,y),(x,z),(z,x) (f:X rightarrow X)`
View Solution`A={1,2,3,4}`மற்றும்`B={a,b,c,d}` எனில் பின்வரும் ஒவ்வொன்றிற்கும்`A rightarrowB` க்கு ஒரு சர்ர்பு உதாரணமாக தருக? ஒன்றுக்கொன்றும் அல்ல மற்றும் மேற்கோர்த்தலும் அல்ல
View Solution`A={1,2,3,4}`மற்றும்`B={a,b,c,d}` எனில் பின்வரும் ஒவ்வொன்றிற்கும்`A rightarrowB` க்கு ஒரு சர்ர்பு உதாரணமாக தருக? ஒன்றுக்கொன்று அல்ல ஆனால் மேற்கோர்த்தல்
View Solution`A={1,2,3,4}`மற்றும்`B={a,b,c,d}` எனில் பின்வரும் ஒவ்வொன்றிற்கும்`A rightarrowB` க்கு ஒரு சர்ர்பு உதாரணமாக தருக? ஒன்றுக்கொன்று ஆனால் மேற்கோர்த்தல் அல்ல
View Solution`A={1,2,3,4}`மற்றும்`B={a,b,c,d} `எனில் பின்வரும் ஒவ்வொன்றிற்கும்`A rightarrowB` க்கு ஒரு சர்ர்பு உதாரணமாக தருக? ஒன்றுக்கொன்று மற்றும் மேற்கோர்த்தல்
View Solution`1/(1-2sinx`என்ற சார்பின் சார்பாகத்தை காண்க
View Solution`f(x)=sqrt(4-x^2)/sqrt(x^2-9)`என்ற சார்பின் மீப்பெரு சார்பாகத்தை காண்க
View Solution`1/(2Cosx-1)`என்ற சார்பின் வீச்சகத்தை காண்க
View Solution`xy=-2`எனும் தொடர்பு தகுந்த சார்பகத்தில் ஒரு சார்பு எனக் காட்டுக. அதன் சார்பகம் மற்றும் வீச்சகம் காண்க
View Solution`f(x)=abs(x)+x`மற்றும் `g(x)=abs(x)-x` என`f,g:RR rightarrowRR` வரையறுக்கப்படின் `gof`மற்றும்`fog` காண்க
View Solution`f,g,h`என்பன`RR` ல் வரையறுக்கப்பட்ட மெய்மதிப்புச் `(f+g)oh=foh+goh`சார்புகளேனின் என நிரூபிக்க. மேலும்`fo(g+h)` பற்றி என்ன கூற இயலும் ?தகுந்த காரணங்களுடன் விடை தருக?
View Solution`f:RR rightarrow RR`என்ற சார்பு`f(x)=3x-5` என வரையறுக்கப்படின் அது ஒரு இருபுறச் சார்பு என நிருபித்து அதன் நேர்மாறு காண்க
View Solutionஒரு மனிதனின் தசைகளின் எடை`W` ஆனது அவரது உடல் எடை `x`ன் சார்பாக அமைகிறது. மற்றும்`W(x)=0.35x` எனவும் குறிக்கப்படுகிறது. எனில், இச்சார்பின் சார்பாகத்தை தீர்மானிக்கவும்
View Solutionமேலிருந்து கீழே விழும் ஒரு பொருளின் உயரம்`t` நேரத்தை பொருத்துச் சார்பாக`s(t)=-16t^2` என அமைகிறது. இச்சார்பினை வரைபடமாகக் கொண்டு ஒன்றுக்கொன்றா எனத் தீர்மானிக்கவும்
View Solutionஒரு குறிப்பிட்ட வான்வழிப் பயணக் கட்டணமானது, அடிப்படை வானுர்திக் (ரூபாயில்)கட்டணம்`C` உடன் எரிபொருள் கூடுதல் கட்டணம் `S`உள்ளடக்கியது. `C`மற்றும் `S`ஆகிய இரண்டுமே வான் தொலைவு `m`ஆல் அமைகிறது மேலும்`C(m)=0.4m+50` மற்றும் `S(m)=0.03m` எனில் வான் தொலைவு அளவு ரீதியாக ஒரு பயணச் சீட்டின் மொத்தமாக கட்டணத்தினை `m`ன் சார்பாக எழுதுக. மேலும் `1600`வான் தொலைவு மைல்களுக்கான பயணச் சீட்டின் தொகையை கான்க
View Solutionஒரு விற்பனை பிரதிநிதியின் ஆண்டு வருமானத்தைக் குறிக்கும் சார்பு `A(x)=30000+0.04x`.இங்கு `x`என்பது அவர் விற்கும் பொருளின் விலைமதிப்பை ரூபாயகக் குறிக்கின்றது. விற்பனைத் துறையில் உள்ள அவர் மகனின் வருமானம் `S(x)=25,000+0.05x`எனும் சார்பாகக் குறிக்கப்படுகிறது எனில்,`(A+S)(x)` காண்க. மேலும் `1,50,00,000`மதிப்புள்ள பொருட்களை அவர்களிருவரும் தனித்தனியே விற்றால் வருமானம்
View Solutionஅமெரிக்கா டாலரை சிங்கப்பூர் டாலராக ஒரு குறிப்பிட்ட நாளில் பண மதிப்பு மாற்றம் செய்யும் சார்பு`f(x)=1.23x` ஆகும் .இங்கு`x` என்பது அமெரிக்க டாலர்களின் எண்ணிக்கை ஆகும் . அதே நாளில் இந்திய ரூபாய்க்கு சிங்கப்பூர் டாலரை மற்றும் சார்பு`g(y)=50.50y` இங்கு`y` என்பது சிங்கப்பூர் டாலர்களின் எண்ணிக்கை ஆகும். இந்திய ரூபாயின் அடிப்படையில் அமெரிக்க டாலரின் நாணயப் பரிவர்த்தனை விகிதத்தை சார்பினை எழுதுக
View Solutionஒரு சிறிய உணவகத்தின் உரிமையாளர் `100`செலவில் ஒரு குறிப்பிட்ட உணவை தயாரிக்க முடியும். உணவு வகைப் பட்டியலின்படி அந்த உணவின் விலை `x`என நிர்ணயித்தால், அந்நாளில் அவ்வுணவைப் பெறும் வாடிக்கையாளர்களின் எண்ணிக்கை`D(x)=200-x` என்ற சார்பாக அமைகிறது. அந்த உணவைப் பொறுத்து அவருடைய அன்றயை வருமானம், மொத்தச் செலவு மற்றும் லாபம் ஆகியவற்றை `x`ன் சார்பாக அமைக்கவும்
View Solutionபாரன்ஹூட்டிலிருந்து செல்சியஸ் வெப்பநிலைக்கு மாற்றும் சார்பு`y=(5x)/9 -160/9` எனில், y ன் நேர்மாறு சார்பினைக் காண்க. நேர்மாறு சார்பும் ஒரு சார்பு எனவும் காண்க
View Solutionஒரு சாதாரண சங்கேத மொழியில் ஓர் உருவினை மாற்றியமைக்க எண்ணால் எழுதப் பயன்படுத்தப்படும் சார்பு `f(x)=3x-4`இச்சார்பின் நேர்மாறினையும், அந்நேர்மாறு ஒரு சார்பு என்பதனையும் காண்க. அவை`y=x` என்ற நேர்கோட்டில் சமச்சீர் உடையது என்பதை வரைந்து காண்க
View Solutionகொடுக்கப்பட்டுள்ள படத்தில்`y=x^3` என்ற வளை வரியின் படத்தினை பயன்படுத்தி அச்சு மதிப்பு மாறாமல் ஒரே தளத்தில் கீழ்காணும் சார்புகளை வரைக(i) `y=-x^3` (ii)`y=x^3+1` (iii)`y=x^3-1` (iv)`y=(x+1)^3`
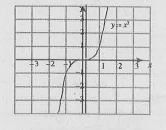
View Solutionகொடுக்கப்பட்டுள்ள படத்தில்`y=x^((1/3))` என்ற வளை வரையைப் பயன்படுத்திக் கீழ்காணும் சார்புகளை ஒரே தளத்தில் வரைக(i) `y=-x^((1/3))` (ii)`y=x^((1/3))+1` (iii)`y=x^((1/3))-1` (iv)`y=(x+1)^((1/3))`
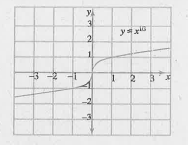
View Solutionஒரே தளத்தில்`f(x)=x^(3)` மற்றும்`g(x)=root(3)(x)` சார்புகளை வரைபடமாக்குக.`fog`ஐ கணித்து அதே தளத்தில் வரைபடமாக்குக.முடிவுகளை ஆய்வு செய்க.
View Solution`y=x^(2)`என்ற வளைவரைவிலிருந்து`y=3(x-1)^2+5` என்ற வளைவரையை காணும் படிநிலைகளை எழுதுக
View Solution`y=sin x`என்ற சார்பினை வரைந்து அதன் மூலம் `y=sin(-x)` என்ற சார்பினை வரைந்து அதன் மூலம் ஆகியவற்றை வரைக. (இங்கு(iii)(iv), என்பவை `cos x`என்பது முக்கோணவியல் மூலம் தெரிந்துகொள்ளலாம்
View Solution`y=sin x`என்ற சார்பினை வரைந்து அதன் மூலம் `y=-sin(-x)` என்ற சார்பினை வரைந்து அதன் மூலம் ஆகியவற்றை வரைக. (இங்கு(iii)(iv), என்பவை `cos x`என்பது முக்கோணவியல் மூலம் தெரிந்துகொள்ளலாம்
View Solution`y=sin x`என்ற சார்பினை வரைந்து அதன் மூலம் `y=sin(pi/2+x)` என்ற சார்பினை வரைந்து அதன் மூலம் ஆகியவற்றை வரைக. (இங்கு(iii)(iv), என்பவை `cos x`என்பது முக்கோணவியல் மூலம் தெரிந்துகொள்ளலாம்
View Solution`y=sin x`என்ற சார்பினை வரைந்து அதன் மூலம் `y=sin(pi/2 -x)`என்ற சார்பினை வரைந்து அதன் மூலம் ஆகியவற்றை வரைக. (இங்கு(iii)(iv), என்பவை `cos x`என்பது முக்கோணவியல் மூலம் தெரிந்துகொள்ளலாம்
View Solution`y=x`என்ற நேர்கோட்டின் மூலம் `y=-x` ஆகியவற்றை தோராயமாக வரைக
View Solution`y=x`என்ற நேர்கோட்டின் மூலம் `y=2x` ஆகியவற்றை தோராயமாக வரைக
View Solution`y=x`என்ற நேர்கோட்டின் மூலம் `y=x+1` ஆகியவற்றை தோராயமாக வரைக
View Solution`y=x`என்ற நேர்கோட்டின் மூலம் `y=1/2x+1` ஆகியவற்றை தோராயமாக வரைக
View Solution`y=absx`என்ற வளைவரையின் மூலம் `y=abs(x-1)+1` ஆகியவற்றை வரைக
View Solution`y=absx`என்ற வளைவரையின் மூலம்`y=abs(x+1)-1`ஆகியவற்றை வரைக
View Solution`y=absx`என்ற வளைவரையின் மூலம் `y=abs(x+2)+3`ஆகியவற்றை வரைக
View Solution`y=sin x`என்ற வளைவரை மூலம்`y=sin absx` என்பதன் வரை படத்தை வரைக [இங்கு sin(-x)=-sin x].
View Solution`A={(x,y):y=e^x,x in RR` மற்றும் `B={(x,y):y=e-x,x in RR` எனில், `n(AcapB)` என்பது
View Solution`A={(x,y):y=sinx,x in RR}`மற்றும் `B={(x,y):y=cosx,x inRR}`எனில்`A∩B`ல்
View Solution`A={0,-1,1,2}` எனும் கணத்தில் `abs(x^2+y^2)le2`எனுமாறு`xRy` ஆக வரையறுக்கப்பட்ட தொடர்பு`R` எனில், கீழ்க்கண்டவற்றில் எது சரியானது ?
View Solution`f(x)=abs(x-2)+abs(x+2),x in RR`எனில்
View Solutionஇயல் எண்களின் அனைத்துக்கணம் `N`க்கு `A`மற்றும்`B` உட்கணங்கள் எனில்`A'cup[(AcapB)cupB']` என்பது
View Solutionகணிதம் மற்றும் வேதியியல் இரண்டும் பாடங்களாக ஏற்ற மாணவர்களின் எண்ணிக்கை `70`.இது கணிதத்தை ஏற்றவர்களின் `10%` மற்றும் வேதியியல் ஏற்றவர்களின் `14%` ஆகும். இவற்றில் ஏதாவதொன்றைப் பாடமாக ஏற்ற மாணவர்களின் எண்ணிக்கை
View Solution`n[{(A xxB)cap(AxxC)]=8`மற்றும்`n(BcapC)=2,` எனில்`n(A)` என்பது
View Solution`n(A)=2`மற்றும் `n(BcupC)=3`எனில்`n[(AxxB)cup(AxxC)]`
View Solution`A`மற்றும்`B` எனும் இரு கணங்களில் `17`உறுப்புகள் பொதுவானவை எனில், `AxxB`மற்றும்`BxxA` ஆகிய கணங்களில் உள்ள பொது உறுப்புகளின் எண்ணிக்கை
View Solutionவெற்றற்ற கணங்கள்`A` மற்றும்`B` என்க`AsubsetB` எனில்`(AxxB)cap(BxxA)=`
View Solution`3`உறுப்புகளை கொண்ட கணத்தின் மீதான தொடர்புகளின் எண்ணிக்கை
View Solutionஒன்றுக்கு மேற்பட்ட உறுப்புகளைக் கொண்ட கணம் `X`ன் மீதான அனைத்துத் தொடர்பு `R`எனில்`R` என்பது
View Solution`X={1,2,3,4}`மற்றும் R={(1,1),(1,2),(1,3),(2,2),(3,3),(2,1),(3,1),(1,4),(4,1)}.எனில்`R` என்பது
View Solution`1/(1-2sinx)`என்ற சார்பின் வீச்சகம்
View Solution`f(x)=|floorx-x|,x in RR`என்ற சார்பின் வீச்சகம்
View Solution`f(x)=x^2`என்ற சார்பு இருபுறச் சார்பாக அமைய வேண்டுமெனில் அதன் சார்பகமும் துணைச் சார்பகமும் முறையே
View Solution`m`உறுப்புகளை கொண்ட ஒரு கணத்திலிருந்து`n` உறுப்புகள் கொண்ட ஒரு கணத்திற்கு வரையறுக்கப்படும் மாறிலிச் சார்புகளின் எண்ணிக்கை
View Solution`f:[0,2pi]rightarrow[-1,1]`எனச் சார்பு,`f(x)=sin x` என வரையறுக்கப்படுகிறது எனில். அது
View Solution`f:[-3,3]rightarrowS`என்ற சார்பு`f(x)=x^(2)` என வரையறுக்கப்பட்டு மேற்கோர்த்தல் எனில், `S`என்பது
View Solution`X={(1,2,3,4},Y={a,b,c,d}`மற்றும் `f={(1,a),(4,b),(2,c),(3,d),(2,d)}`எனில் `f` என்பது
View Solutionதீர்க்க
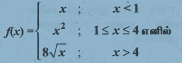
View Solution`f:RRrightarrowRR`என்ற சார்பு,`f(x)=1-absx` எனில் `f`ன் வீச்சகம்
View Solution`f:RRrightarrowRR`ல்`f(x)=sin x+cos x` எனில்`f` ஆனது
View Solution`f:RRrightarrowRR-f(x)=((x^2+cosc)(1+x^4))/((x-sin x)(2x-x^3)) `எனில்,`f`
View Solution`f:RR rightarrowRR`ஆனது`f(x)=x^4`என வரையறுக்கப்படுகிறது.பொருத்தமான விடையைத் தேர்ந்தெடுக்க
View Solution
EXERCISE questions and complete solutions for chapter கணங்கள்,தொடர்புகள் மற்றும் சார்புகள் of SURA MATHS (TAMIL) of Class 11