Complete Solutions to EXERCISE of chapter வகை நுண்கணிதம் வகைமை மற்றும் வகையிடல் முறைகள் of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | வகை நுண்கணிதம் வகைமை மற்றும் வகையிடல் முறைகள் |
| SURA PUBLICATION(TAMIL) | EXERCISE |
| Number Of Questions | 100 |
| Academic Year | 2023-24 |
முதல் கொள்கையினைப் பயன்படுத்திப் பின்வரும் சார்புகளின் வகைக்கெழுக்களைக் காண்க. (i) `f(x) = 6` (ii) `f(x) = -4x+7` (iii) `f(x) = x^2+2`
View Solutionகீழ்காணும் சார்புகளுக்கு x = 1-ல் இடப்பக்க மற்றும் வலப்பக்க வகைக்கெழு(கிடைக்கப்பெறின்) காண்க. x =1-ல் சார்புகளுக்கு வகைமைத்தன்மை உள்ளதா என்பதனையும் காண்க. (i) `f(x) = |x-1|` (ii) `f(x) = sqrt(1-x^2)` (iii) `f(x) = {(x,,xle1), (x^2,,x>1):}`
View Solutionகொடுக்கப்பட்ட புள்ளிகளில் கீழ்காணும் சார்புககள் வகைமையானதா என்பதைத் தீர்மானிக்கவும்.(i) `f(x) = x|x|, x=0` (ii) `f(x) = |x^2-1|, x=1` (iii) `f(x) =|x|+|x-1|, x=0,1` (iv) `f(x) = sin|x|, x=0`
View Solutionகீழ்காணும் சார்புகளுக்கு குறிப்பிடப்பட்டுள்ள புள்ளிகளில் வகைமை இல்லை என்பதை நிறுவுக. (i) `f(x) ={(-x+2,,xle2), (2x-4,,x>2):},x=2` (ii) `f(x) ={(3x,,x<0), (-4x,,xge0):},x=0`
View Solutionதரப்பட்டுள்ள f-ன் வரைபடத்தில் எந்தெந்த x -ன் மதிப்புகளுக்கு (எண்களுக்கு) f வகைமை இல்லை என்பதனையும் அதற்கான காரணங்களையும் கூறுக.
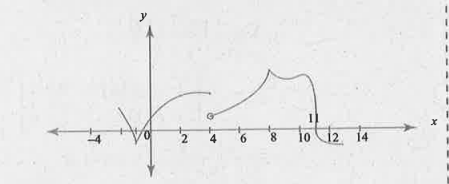
View Solution`f(x)= |x+100|+x^2` எனில் ,f'(-100) கிடைக்கப்பெறுமா எனச் சோதித்து பார்க்கவும்.
View Solutionகீழ்காணும் சார்புகளின் வகைமைத் தன்மையைப் படங்கள் வரைந்து `RR`-ல் பரிசோதிக்கவும். (i) `|sin x|` (ii) `|cos x|`.
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `f(x)= x-3sin x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y= sin x+ cos x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `f(x) = x sin x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = cos x-2tan x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `g(t) = t^3 cos t`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `g(t) = 4sec t + tan t`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = e^x sin x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = tanx/x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = sinx/(1+cosx)`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = x/(sinx+cosx)`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = (tanx-1)/(secx)`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = (sinx)/(x^2)`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = tan theta(sin theta + cos theta)`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = cosec x.cot x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = xsin x cos x`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = e^(-x)logx`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = (x^2+5).In(1+x)e^(-3x)`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = sinx^@`
View Solutionபின்வரும் சார்புகளை தொடர்புடைய சாரா மாறிகளைப் பொறுத்து வகையிடுக. `y = log_10x`
View Solution`f(x) = 2x^2-5x+3` எனில் f'(x) என்ற சார்பின் வரைபடம் வரைக.
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = (x^2+4x+6)^5`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = tan3x`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = cos(tanx)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = root(3)(1+x^3)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = e^sqrtx`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = sin(e^x)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `F(x) = (x^3+4x)^7`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `h(t) = (t-1/t)^(3/2)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `f(t) = root(3)(1+tant)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = cos(a^3+x^3)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = e^(-mx)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = 4sec5x`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y = (2x-5)^4(8x^2-5)^(-3)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=(x^2+1)root(3)(x^2+2)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=xe^(-x^2)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `s(t)=root(4)((t^3+1)/(t^3-1))`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `f(x)=x/sqrt(7-3x)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=tan(cosx)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sin^2x/cosx`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=5^((-1)/x)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sqrt(1+2tanx)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sin^3x+cos^3x`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sin^2(coskx)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=(1+cos^2x)^6`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=e^(3x)/(1+e^x)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sqrt(x+sqrtx)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=e^(xcosx)`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sqrt(x+sqrt(x+sqrtx))`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sin(tan(sqrtsinx))`
View Solutionகீழ்க்காணும் சார்புகளுக்கு வகைக்கெழுக்களைக் காண்க. `y=sin^(-1)((1-x^2)/(1+x^2))`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `y=x^(cosx)`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `y=x^(logx)+(logx)^x`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `sqrt(xy)=e^((x-y))`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `x^y=y^x`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `(cosx)^logx`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `x^2/a^2+y^2/b^2=1`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `sqrt(x^2+y^2)=tan^(-1)(y/x)`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `tan(x+y)+tan(x-y)=x`
View Solution`cos(xy)=x` எனில், `dy/dx=-((1+ysin(xy)))/(xsin xy)` எனக்காட்டுக .
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `tan^(-1)sqrt((1-cosx)/(1+cosx)).`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `tan^(-1)((6x)/(1-9x^2)).`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக.`cos(2tan^(-1)(sqrt((1-x)/(1+x)))).`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `x=acos^3t, y=asin^3t`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `x=a(cost+tsint), y=a(sint-tcost)`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `x= (1-t^2)/(1+t^2), y= (2t)/(1+t^2)`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `cos^(-1)((1-x^2)/(1+x^2))`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `sin^(-1)(3x-4x^3)`
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `tan^(-1)((cosx+sinx)/(cosx-sinx)).`
View Solution`x^2`-ஐ பொறுத்து `sinx^2`-ன் வகைக்கெழுவைக் காண்க.
View Solution`tan^(-1) x`-ஐ பொறுத்து `sin^(-1)((2x)/(1+x^2))`-ன் வகைக்கெழுவைக் காண்க.
View Solution`u=tan^(-1) ((sqrt(1+x^2)-1)/(x)),v=tan^(-1)x` எனில் `(du)/(dv)` காண்க.
View Solution`tan^(-1) ((cosx)/(1+sinx))`-ஐ பொறுத்து `tan^(-1) ((sinx)/(1+cosx))`-ன் வகைக்கெழுவைக் காண்க.
View Solution`y=sin^(-1)x` எனில் , `y` ` `"` ` காண்க.
View Solution`y=e^(tan^(-1)x)` எனில், `(1+x^2)y^`"`+(2x-1)y'=0` எனக்காட்டுக.
View Solution`y=sin^(-1)x/sqrt(1-x^2)` எனில், `(1-x^2)y_2-3xy_1-y=0` எனக்காட்டுக
View Solution`x=a(theta+sintheta), y=a(1-costheta)` எனில்,`theta=pi/2` எனும்போது `y''=1/a` என நிரூபிக்க.
View Solution`sin y=xsin(a+y)`எனில், `dy/dx=(sin^2(a+y))/sina` என நிரூபிக்க. இங்கு `a!=npi`.
View Solution`y=(cos^(-1)x)^2` எனில், `(1-x^2)(d^2y)/(dx^2)-xdy/dx-2=0` என நிரூபிக்க. மேலும் x=0-ன் போது `y_2` மதிப்பைக் காண்க.
View Solution`d/dx(2/pisinx^@)`
View Solution`y=f(x^2+2)` மற்றும் `f '(3)=5` எனில், x=1-ல் `dy/dx` என்பது
View Solution`y=1/4u^4, u=2/3x^3+5` எனில், `dy/dx` என்பது
View Solution`f(x)=x^2-3x` எனில்,`f(x)=f ' (x)` என அமையும் புள்ளிகள்
View Solution`y=1/(a-z)` எனில்,` dz/dy`-ன் மதிப்பு
View Solution`y=cos(sinx^2)` எனில் `x=sqrt(pi/2)`-ல் `dy/dx`-ன் மதிப்பு
View Solution`y=mx+c` மற்றும் `f(0)=f'(0)=1` எனில், f(2) என்பது
View Solution`f(x)=xtan^(-1)x` எனில், f'(1) என்பது
View Solution`d/dx(e^(x+5logx))` என்பது
View Solution`x=0` -ல் `(ax-5)e^(3x)`-ன் வகைக்கெழு -13 எனில், `a` - ன் மதிப்பு
View Solutionகீழ்க்காண்பவற்றை வகையிடுக. `x= (1-t^2)/(1+t^2), y= (2t)/(1+t^2)`
View Solution`x=asintheta` மற்றும் `y=bcostheta`எனில், `(d^2y)/dx^2` என்பது
View Solution`log_x10`-ஐ பொறுத்து `log_10x`-ன் வகைக்கெழு
View Solution`f(x)=x+2` எனில்,x=4-ல்`f'(f(x))`-ன் மதிப்பு
View Solution`y=(1-x)^2/x^2` எனில், `dy/dx`-ன் மதிப்பு
View Solution
EXERCISE questions and complete solutions for chapter வகை நுண்கணிதம் வகைமை மற்றும் வகையிடல் முறைகள் of SURA MATHS (TAMIL) of Class 11