Complete Solutions to MCQ (COMPETITIVE THINKING) of chapter FRICTION IS SOLIDS AND LIQUIDS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | FRICTION IS SOLIDS AND LIQUIDS |
| TARGET PUBLICATION | MCQ (COMPETITIVE THINKING) |
| Number Of Questions | 98 |
| Academic Year | 2023-24 |
Which one of the following is NOT used to reduce friction ?
View SolutionSTATEMENT-1: It is easier to pull a heavy object than to push it on a level ground and
STATEMENT-2: The magnitude fo frictional force depends on the nature of the two surfaces in contact.
View SolutionIf a ladder weighting `250 N` is placed against a smooth vertical wall having coefficient of friction between it and floor 0.3, then what is the maximum force of friction available at the point of contact between the ladder and the floor?
View SolutionThe coefficient of static friction, `mu_(s)` between block A of mass 2 kg and the table as shown in the figure is 0.2. What would be the maximum mass value of block B so that the two blocks do not move? The string and the pulley are assumed to be smooth and massless.`(g=10m//s^(2))`

View SolutionA lift is moving down with an acceleration equal to the acceleration due to gravity. A body of mass `M` kept on the floor of the lift is pulled horizontally If the coefficient of friction is `mu` then the frictional resistance offered by the body is .
View SolutionMaximum acceleration of the train in which a 50 kg box lying on its floor will ramain stationary is (Given: Co-efficient of static friction between the box and the train's floor is `0.3 and g =10ms^(-2))`
View SolutionA block `B` is pushed momentarily along a horizontal surface with an initial velocity `v` . If mu is the coefficient of sliding friction between `B` and the surface, block `B` will come to rest after a time:

View SolutionA block rests on a rough inclined plane making an angle of `30^@` with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA wooden box of mass `8kg` slides down an inclined plane of inclination `30^(@)` to the horizontal with a constant acceleration of `0.4ms^(-2)` What is the force of friction between the box and inclined plane ? `(g = 10m//s^(2))` .
View SolutionA wooden box lying at rest on an inclined surface of a wet wood is held at static equilibrium by a constant force `vec F` applied perpendicular to the incline. If the mass of the box is 1 kg, the angle of inclination is `30^(@)` and the coefficient of static friction between the box and the inclined plane is `0.2,` the minimum magnitude of `vecF` is (Use `g= 10m//s^(2))`
View SolutionWhat is the maximum value of the force F such that the block shown in the arrangement, does not move?
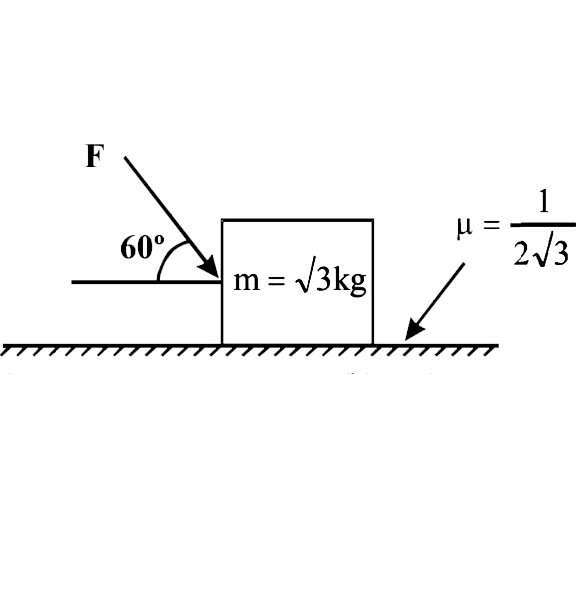
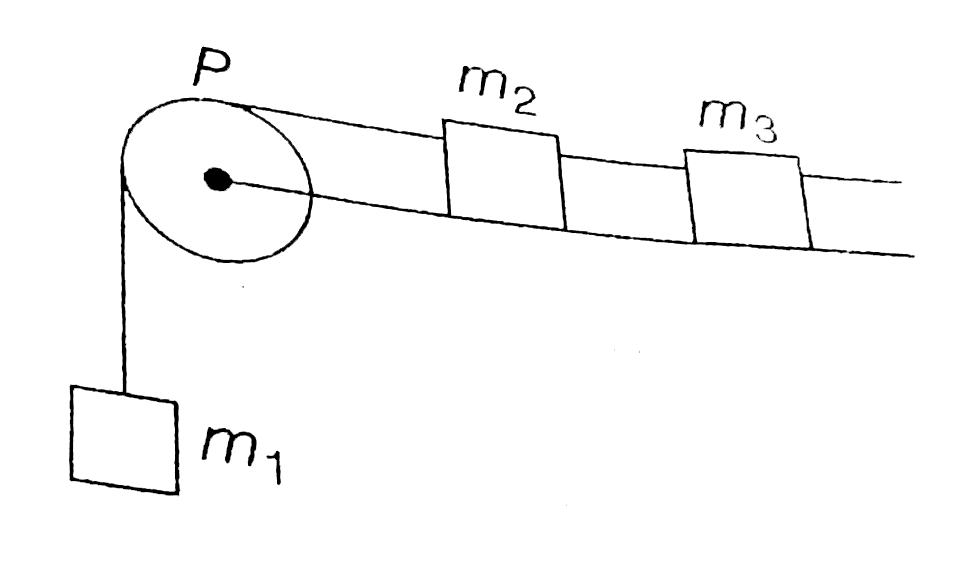
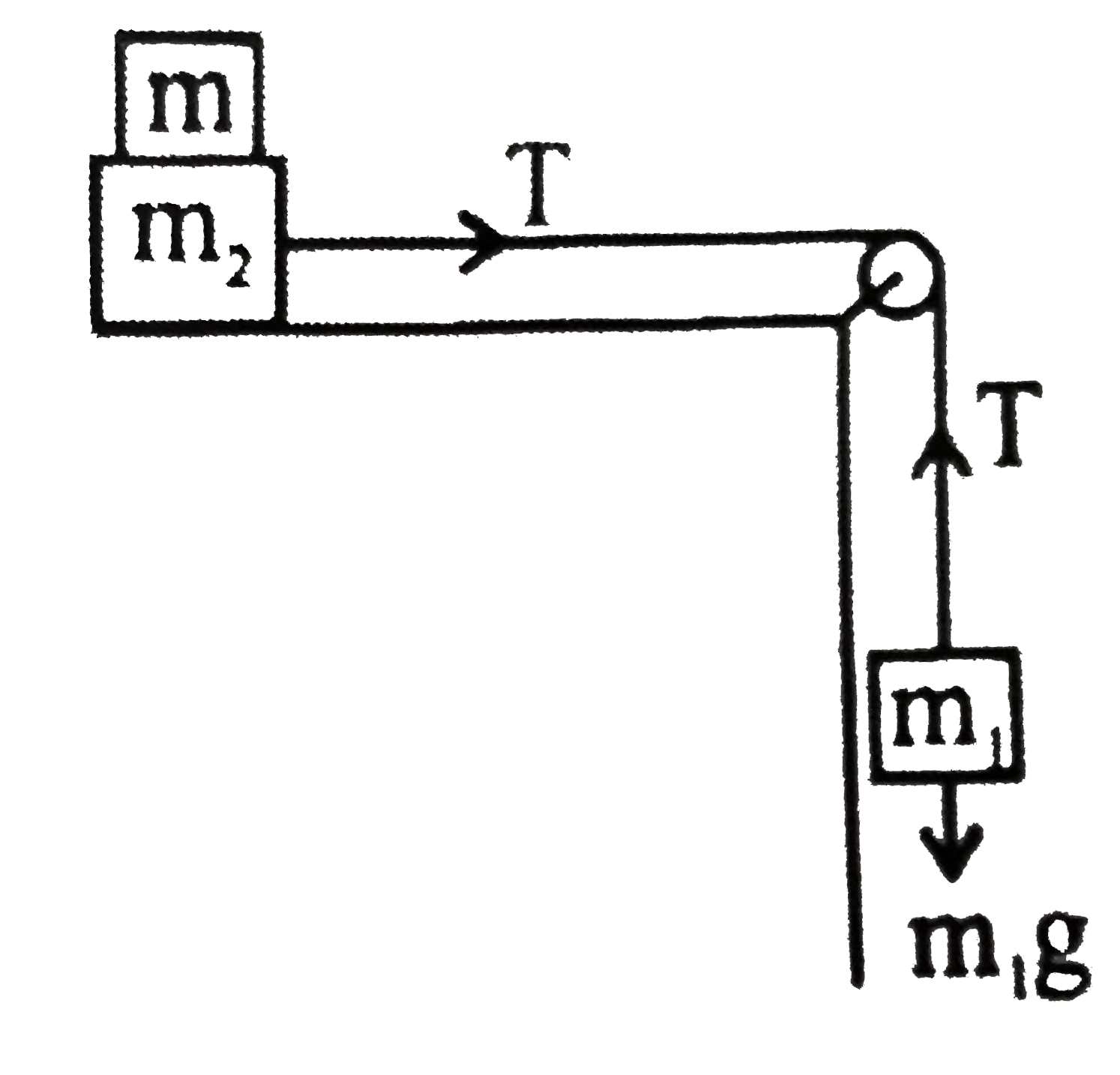
View SolutionA system consists of three masses `m_(1),m_(2) " and " m_(3)` connected by a string passing over a pulley P. The mass `m_(1)` hangs freely and `m_(2) " and " m_(3)` are on a rough horizontal table (the coefficient of friction=`mu`). The pulley is frictionless and of negligible mass. The downward acceleration of mass `m_(1)` is (assume, `m_(1)=m_(2)=m_(3)=m`)
View SolutionMaximum value of static friction is .
View SolutionWhich of the following statements is incorrect ?
View SolutionA body of mass M is kept n a rough horizontal surfasce (friction coefficient `=mu`). A person is trying to pull he body by applying a horizontal force but the body is not moving. The force by the surface on A is F, where
View SolutionConsider a frictionless ramp on which a smooth object is made to side down from an initial height 'h'. The distance 'd' necessary to stop the object on a flat track ( or coefficient of friction `'mu'),` kept at the ramp end is
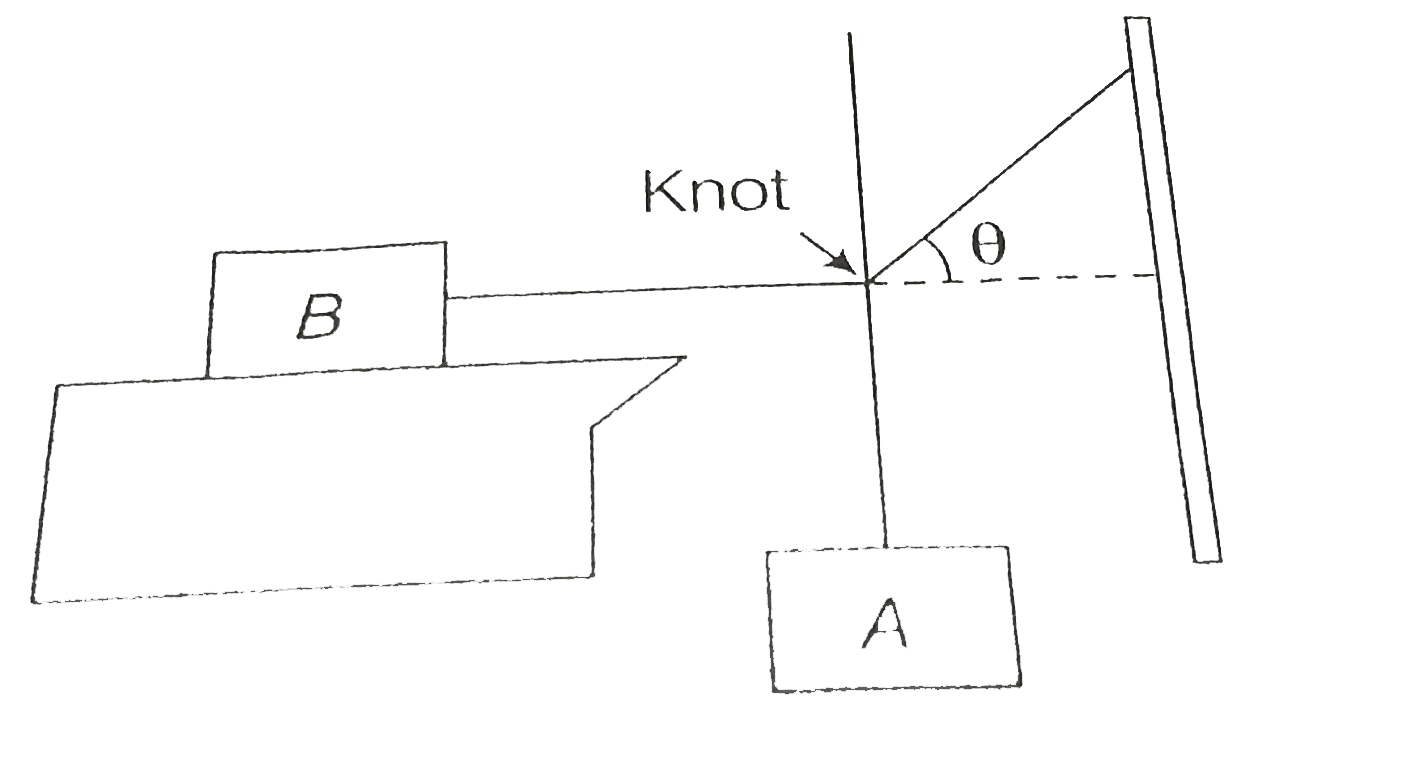
View SolutionBlock B lying on a table weighs w. The coefficient of static friction between the block and the table is µ. Assume that the cord between B and the knot is horizontal. The maximum weight of the block A for which the system will be stationary is
View SolutionA heavy uniform chain lies on a horizontal table-top. If the coefficient of friction between the chain and table surface is 0.25, then the maximum fraction of length of the chain, that can hang over one edge of the table is
View SolutionA block `A` with mass 100kg is resting on another block `B` of mass 200kg. As shown in figure a horizontal rope tied to a wall hold it. The coefficient of friction between `A` and `B` is `0.2` while coefficient of friction between `B` and the ground is `0.3` . the minimum required force `F` to start moving `B` will be.

View SolutionA block of mass `2kg` is kept on the floor. The coefficient of static friction is `0.4` . If a force `F` of `2.5N` is applied on the block as shown in the figure, the frictional force between the block and the floor will be.

View SolutionGiven in figure are two blocks A and B of weight 20N and 100N, respectively. These are being pressed against a wall by a force F as shown. If the coefficient of friction between the blocks is 0.1 and between block B and the wall is 0.15, the frictional force applied by the wall on block B is:

View SolutionA block of mass m is lying on horizontal surface of coefficient of friction `mu.` A force is applied to the block at an angle `theta` with the horizontal. The block will move with a minimum force F if
View SolutionA marble block of mass 2 kg lying on ice when given a velocity of `6m//s` is stopped by friction in 10s. Then the coefficient of friction is
View SolutionA block of mass `m_(2)` is placed on a horizontal table and another block of mass `m_(1)` is placed on top is it. An increasing horizontal force `F = alpha t` is exerted on the upper block but the lowwer block never moves as a result. If the coefficient of friction between the blocks is `mu_(1)` coefficient of friction between the blocks is `mu_(1)` and that between the lower block and the table is `mu_(2),` then what is the maximum possible value of `mu_(1)//mu_(2)` ?
View SolutionA block of mass `m=5kg` is resting on a rough horizontal surface for which the coefficient of friction is `0.2` . When a force `F=40N` is applied, the acceleration of the block will be `(g=10m//s^(2))` .

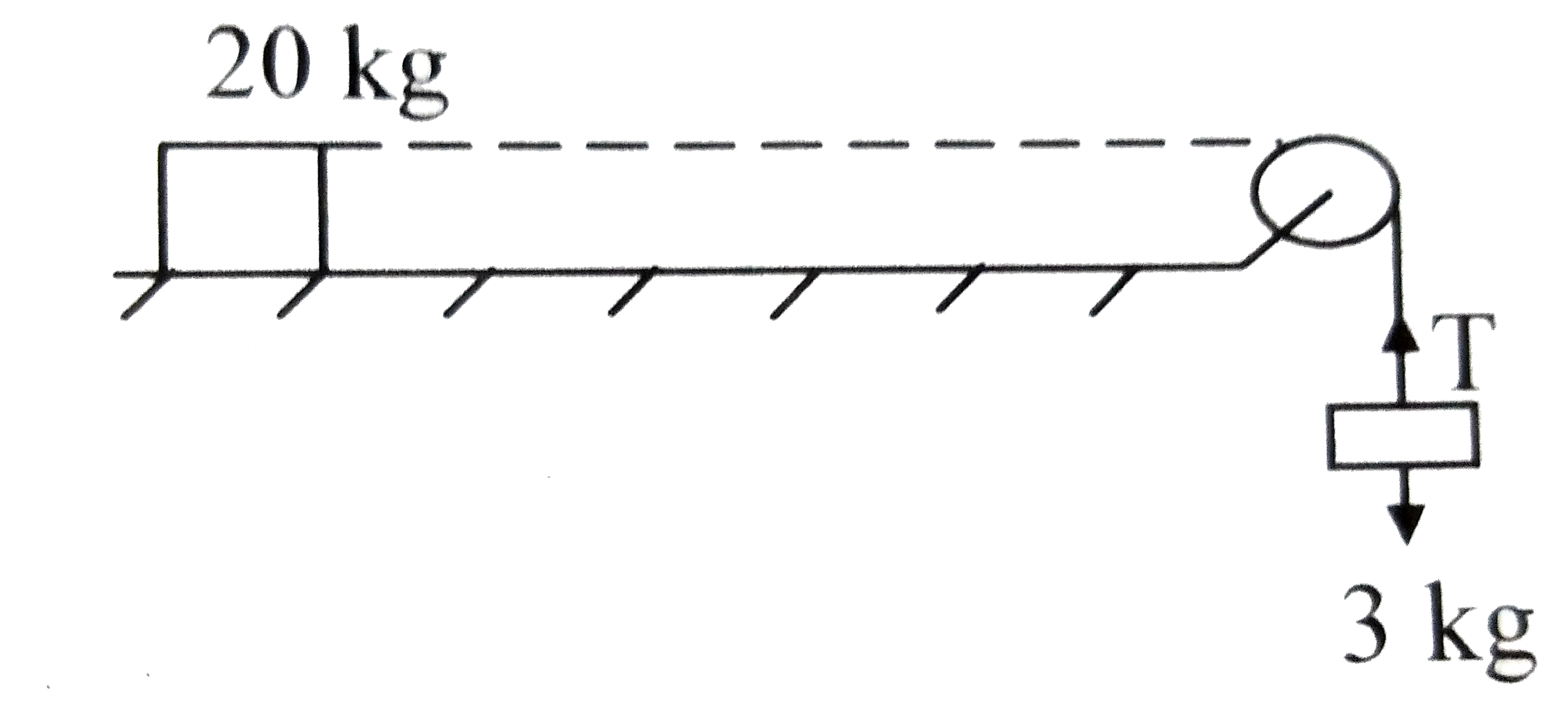
View SolutionA body of mass 20 kg is moving on a rough horizxontal plane. A block of mass 3 kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The coefficient of kinetic friction between the heavier mass and teh surface is
`(g=10m//s^(2)).`
View SolutionA block `A` of mass `m_(1)` rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of table and from its other end another block `B` of mass `m_(2)` is suspended. The coefficient of knetic friction between the block and table is `mu_(k)` . When the block `A` is sliding on the table, the tension in the string is.
View SolutionTwo moasses `m_(1)=5kg and m_(2)=10kg,` connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of horizontal surface is `0.15.` The minimum weitght m that should be put on top of `m_(2)` to stop the motion is :-
View SolutionAir is blown through a hole on a closed pipe containing liquid. Then the pressure will
View SolutionThe pressure at the bottom of a tank of liquid is not proprtional to
View SolutionIf the atompspheric pressure is `P _(a)` then the jpressure P at depth a below the surface of a liquid of density `rho` open to the atmosphere is
View SolutionBy sucking a straw a student can reduce the pressure in his lungs to `750 mm` of `Hg ("density")= 13.6 kg//cm^(3))` Using the straw, he can drink water from a glass up to a maximum depth of :
View SolutionIf pressure at half the depth of a lake is equal to 2//3 pressure at the bottom of the lake then what is the depth of the lake ?
View SolutionThe pressure on a swimmer 10 m below the surface of lake is `"_____"``(g =10m//s^(2), ` atmospheric pressure `=1.01 xx10^(5)Pa)`
View SolutionA U-tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water. Is poured into one side until it stands at a distance of `10 mm` above the water level on the other side. Meanwhile the water rises by `65mm` from its original level (see diagram). The density of the oil is:

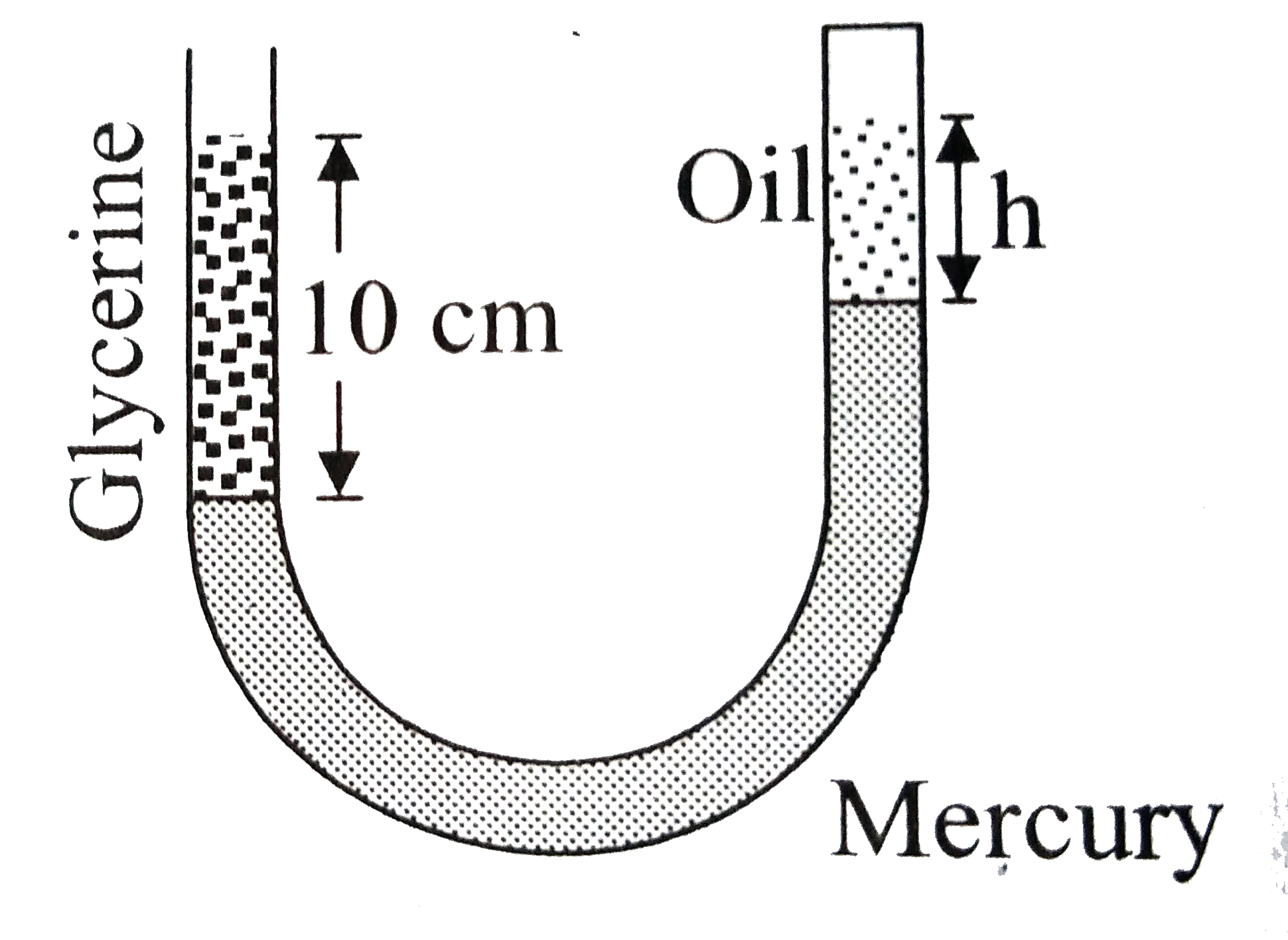
View SolutionA vertical U-tube of uniform inner cross section contains mercury in both sides of its arms. A glycerin (density `=1.3 g//cm ^(3))` column of length 10 cm is introduced into one of its arms. Oil of density 0.8 `gm //cm^(3)` is poured into the other arm until the upper surfaces of the oil and glycerin are in the same horizontal level. Find the length of the same horizontal level. Find the length of the oil column, Density of mercury `=13.6 g//cm^(3)`
View SolutionA manometer connected to a closed tap reads `4.5 xx 10^(5)` pascal. When the tap is opened the reading of the manometer falls is `4 xx 10^(5)` pascal. Then the velocity of flow of water is
View SolutionClouds appear to float in air due to
View SolutionViscosity is a transport phenomenon explained using the concept of transfer of
View SolutionMore viscous oil is used in summer than in winter in motors due to
View SolutionA viscous fluid is flowing through a cylindrical tube. The velocity distribution of the fluid is best represented by the diagram
View SolutionIn stream line flow of liquid, the total energy of liquid constant at `"______".`
View SolutionStatement-1 : The stream of water flowing at high speed from a garden hose pipe tends to spread like a foundtion when held vertically up, but tends to narrow down when held vertically down.
Statement-2 : In any steady flow of an incompressible fluid, the volume flow rate of the fluid remain constant.
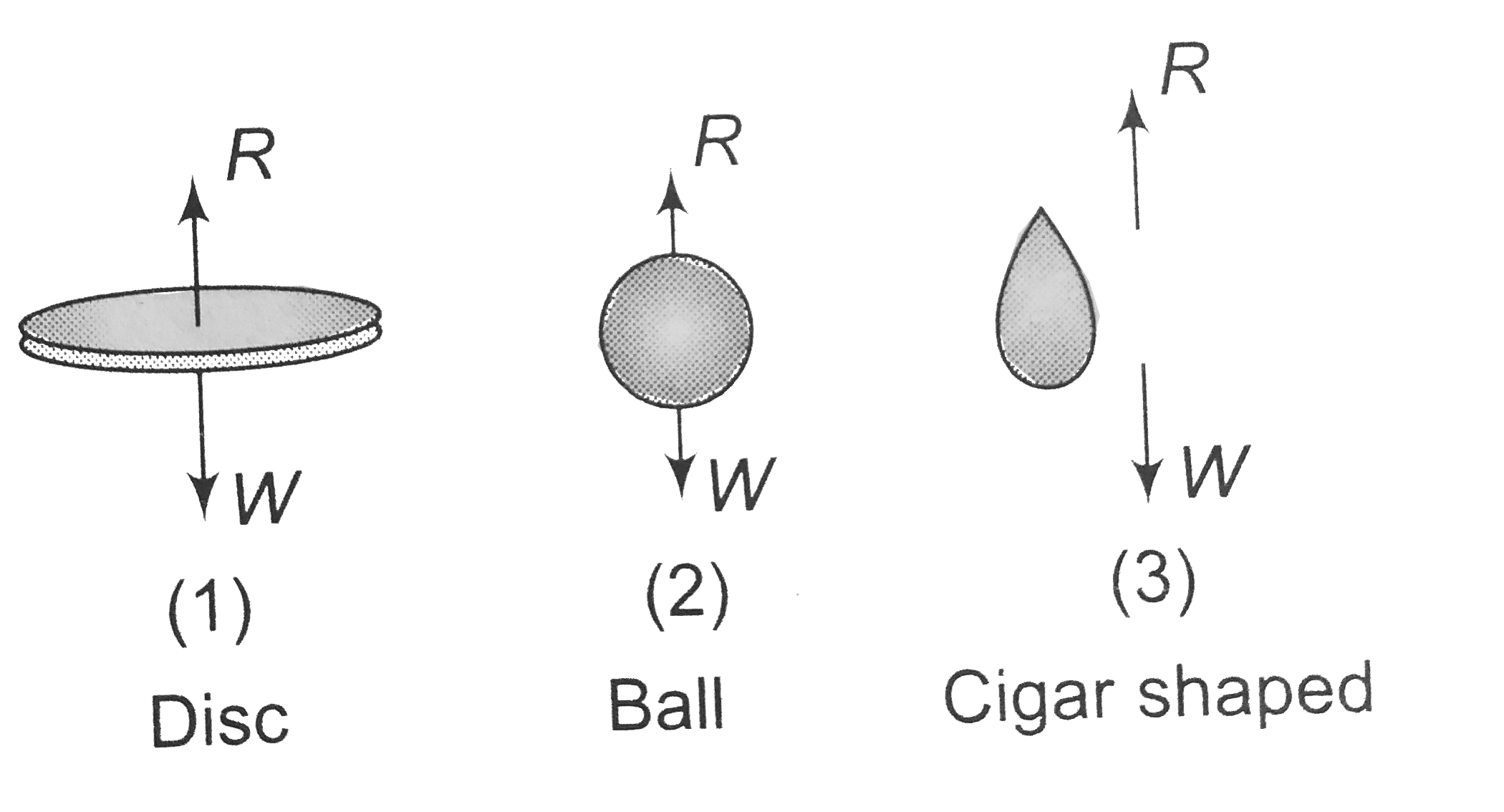
View SolutionWhen a body falls in air, the resistance of air depends to a great extent on the shape of the body, 3 different shapes are gives. Identify the combination of air resistances which truly represents the physical situation. (the cross sectional areas are the same).
View SolutionWater is flowing through a tube of non-uniform cross-section ratio of the radius at entry and exit end of the pipe is `3 : 2`. Then the ratio of velocities at entry and exit of liquid is
View SolutionAn ideal fluid flows through a pipe of circular cross section with diameters 5 cm and 10 cm as shown. The ratio of velocities of fluid at A and B is

View SolutionThe cylindrical tube of a spray pump has radius `R`, one end of which has `n` fine holes, each of radius `r`. If the speed of the liquid in the tube is `V`, the speed of the ejection of the liquid through the holes is:
View SolutionWater is flowing continuously from a tap having an internal diameter `8xx10^(-3)`m. The water velocity as it leves the tap is `0.4 ms^(-1)`. The diameter of the water stream at a distance `2xx10^(-1)`m below the tap is close to `(g=10m//s^(2))`
View SolutionVelocity of water in a river is
View SolutionThe velocity of water in river is 9 km/h of the upper surface . The river is 10 m deep . If the coefficient of viscosity of water is `10^(-2) ` poise then the shearing stress between horizontal layers of water is
View SolutionA metal plate of area `500 cm^92)` is kept on a horizontal surface with a layer of oil of thickness `0.5` mm between them. The horizontal force required to drag the plate with a velocity of 2 cm/s is
(coefficient of viscosity `=0.9` kg/ms)
View SolutionSpherical balls of radius 'R' are falling in a viscous fluid of viscosity `'eta'` with a velocity 'v'. The retarding viscous force acting on the spherical ball is
View SolutionA gas bubble of 2 cm diameter rises through a liquid `1.75 gm cm^(-3)` with a fixed speed of `0.35 cm s^(-1)`.Naglect the density of the gas. The cofficient of viscosity of the liquid is
View SolutionWhat will be the approximate terminal velocity of a rain drop of diamteter `1.8xx 10^(-3)m,` when density of rain water `~~10^(3)kgm^(-3)` and the co-efficient of viscosity of air `~~1.8xx10^(-5)Nsm^(-2)` ? (Neglect buoyancy of air. )
View SolutionA solid ball of volume V is dropped in a viscous liquid. It experiences a viscous force F. If the solid ball of volume 2V of same material is dropped in the same fluid, then the viscous force acting on it will be
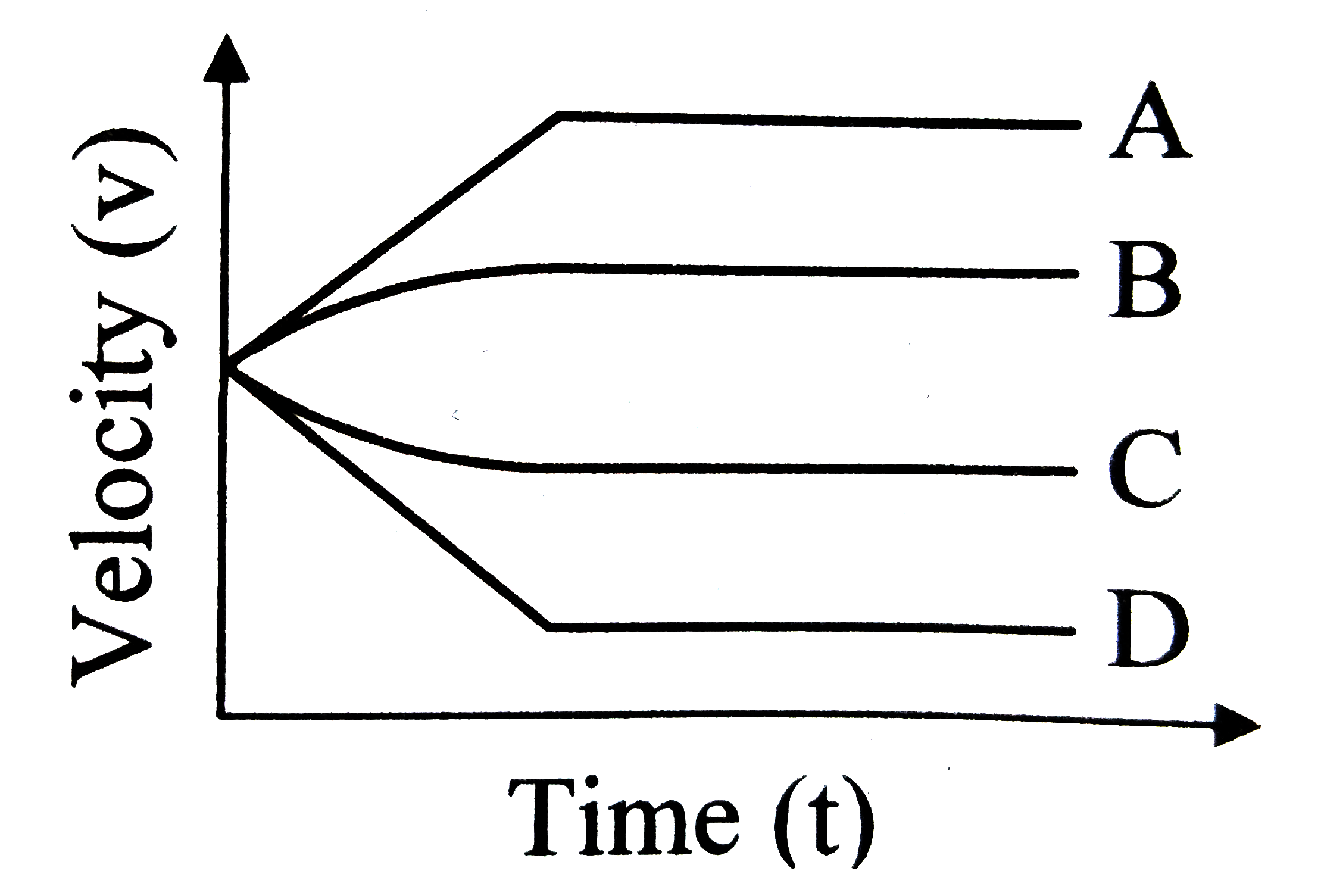
View SolutionA small spherical solid ball is dropped from a great height in a viscous liquid . Its journey in the liquid is best described in the diagram given below by the
View SolutionA small metal ball of mass m is dropped in a liquid contained in a vessel , attains a terminal velocity v . If a metal ball of same material but of mass 8 m is droped is same liquid then the terminal velocity will be
View SolutionA small sphere of mass m is dropped from a height After it has fallen 100 m it has attained its terminal velocity and continues to fall at that speed. The work done by air friction against the sphere during the first 100 m of fall is-
View SolutionThe terminal speed of a sphere of gold (density = 19.5 kg `m^(-3)`) is 0.2 `ms^(-1)` in a viscous liquid (density = 1.5 kg `m^(-3)`). Then, the terminal speed of a sphere of silver (density = 10.5 kg `m^(-3)`) of the same size in the same liquid is
View SolutionTwo solid spheres of same metal but of mass M and 8M fall simultaneously on a viscous liquid and their terminal velocitied are v and n v, then value of n is
View SolutionTwo spheres of equal masses but radii `r_(1) and r_(2)` are allowed to fall in a liquid of infinite are allowed to fall in a liquid of infinite column. The ratio of their terminal velocities are
View SolutionTwo drops of the same radius are falling through air with a steady velcoity of `5 cm s^(-1).` If the two drops coalesce, the terminal velocity would be
View SolutionThe onset of turbulence in a liquid is determined by
View SolutionThe dimensions of Reynold’s constant are
View SolutionThe speed at which the flow of water in a long cylindrical pipe of diameter 2 cm becaomes turbulent is
(The viscosity of water `=1 xx10^(-3)`Pa. s and for the onset of turbulent flow in a long cylindrical pipe, Reynolds number =3000)
View SolutionA horizontal pipeline carrying gasoline has a cross-sectional diameter of 5 mm. If the viscosity and density of the gasoline are `6xx10^(-3)` poise and 720 `kg//m^(3)` respectively, the velocity after which the flow becaomes turbulent is
View SolutionThe water flows form a tap of diameter `1.25` cm with a rate of `5xx10^(-5) m^(3) s^(-1).` The density and coefficient of viscosity of water are `10^(3)kg m ^(-3) and 10^(-3)` Pa. s respectively. The flow of water is
View SolutionConsider the following equation of Bernoulli's theorem.
`P + (1)/(2) rho v^(2) + rhogh = K` (constant)
The dimensions of K/P are same as that of which of the following
View SolutionWater flows steadily through a horizontal pipe of variable cross-section. If the pressure of water is `p` at a point where the velocity of flow is `v`, at another point (pressure `p'`), where the velocity of flow in `2v` : The following statements are given below for P' is
View SolutionA manometer connected to a closed tap rads `4.5 xx10^(5)` pascal. When the tap is opened the reading of the manometer falls to `4xx10^(5)` pascal. Then the velocity of flow of water is
View SolutionA wind with speed `40 m//s` blows parallel to the roof of a house. The area of the roof is `250 m^(2)` . Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be : `(rho_(air)=1.2 kg//m^(3))`
View SolutionWater is filled in a cylindrical container to a height of `3m`. The ratio of the cross-sectional area of the orifice and the beaker is `0.1`. The square of the speed of the liquid coming out from the orifice is `(g=10m//s^(2))`.

View SolutionA cylindrical tank having cross-sectional area A is filled with water to a height of `2.0` m. A circular hole of corss-section area is opened at a height of 75 cm from the bottom. If `a//A=sqrt(0.2,` then velocity with which waer emerges from the hole is
`(g =9.8 ms^(-2))`
View SolutionA cylindrical vessel of 100 cm height is kept filled upto the brim. It has four holes 1,2,3,4 which are respectively at heights of 27 cm, 30 cm , 50 cm and 80 cm from the horizontal floor. The water falling at the maximum horizontal distance from the vessel comes from
View SolutionA cylinder of height h is filled with water and is kept on a block of height `h/2.` The level of water in the cylinder is kept constnat. Four holes numbered `1,2,3,` and 4 are at the side of the cylinder and at heights `0,. h/4, h/2 and (3h)/(4)` respectively. When all four hles are opened together, the hole from which water will reach farthest distnace on the plane PQ is the hole no.

View SolutionA roller is made by joining together two cones at their vertices O, ti is kept on two rails AB and CD, which are placed asymmetrically with its axis perpendiuclar to CD and its center O at the centre of line joining AB and Cd it is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown As it moves, the roller wil tand to:
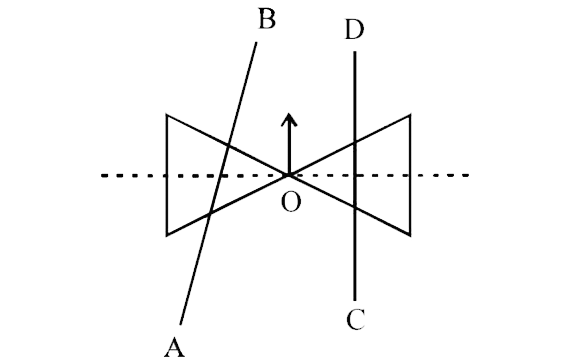
View SolutionThe coefficient of static and dynamic friction between a body and the surface are 0.75 and 0.5 respectively. A force is applied to the body to make it just slide with a constant acceleration which is
View SolutionA body of mass `M` is resting on a rough horizontal plane surface the coefficient of friction being equal to `mu` At `t = 0` a horizontal force `F = F_(0) t` starts acting on it , where `F_(0)` is a constant find the time T at which the motion starts?
View SolutionA plank with a box on it at one end is gradully raised about the other end. As the angle of inclination with the horizntal reaches `30^(@)` , the box starts to slip and slide `4.0m` down the plank in `4.0s` . The coefficients of static and knitic friction between the box and the plank will be, respectively.

View SolutionThere is a small hole at the bottom of tank filled with water. If total pressure at the bottom is `3 atm(1 atm=10^(5)Nm^(-2))`, then find the velocity of water flowing from hole.
View SolutionThe working of venturimeter is based on
View SolutionIn dimension of circal velocity `v_(0)` liquid following through a take are expressed as `(eta^(x) rho^(y) r^(z))` where `eta, rhoand r `are the coefficient of viscosity of liquid density of liquid and radius of the tube respectively then the value of `x,y` and `z` are given by
View SolutionThe upper half of an inclined plane with inclination `phi` is perfectly smooth while the lower half is rough. A body starting from rest at the top will again come to rest at the bottom if the coefficient of friction for the lower half is given by
View SolutionA bullet of mass 50 g moving horizontally with a velocity `210 ms^(-1)` gets embedded in a block of mass 1 kg kept on a rough horizontal surface. If the coefficient of kinetic friction between the block and surface is `0.5.` The block- bullet system will move a distance of `"______"` before coming to res t(Acceleration due to gravity `=10 ms^(-2)).`
View SolutionA body of weight 64 N is pushed with just enough force to start it moving across a horizontal floor and the same force continues to act afterwards. If the coefficients of static and dynamic friction are 0.6 and 0.4 respectively, the acceleration of the body will be (Acceleration due to gravity = g)
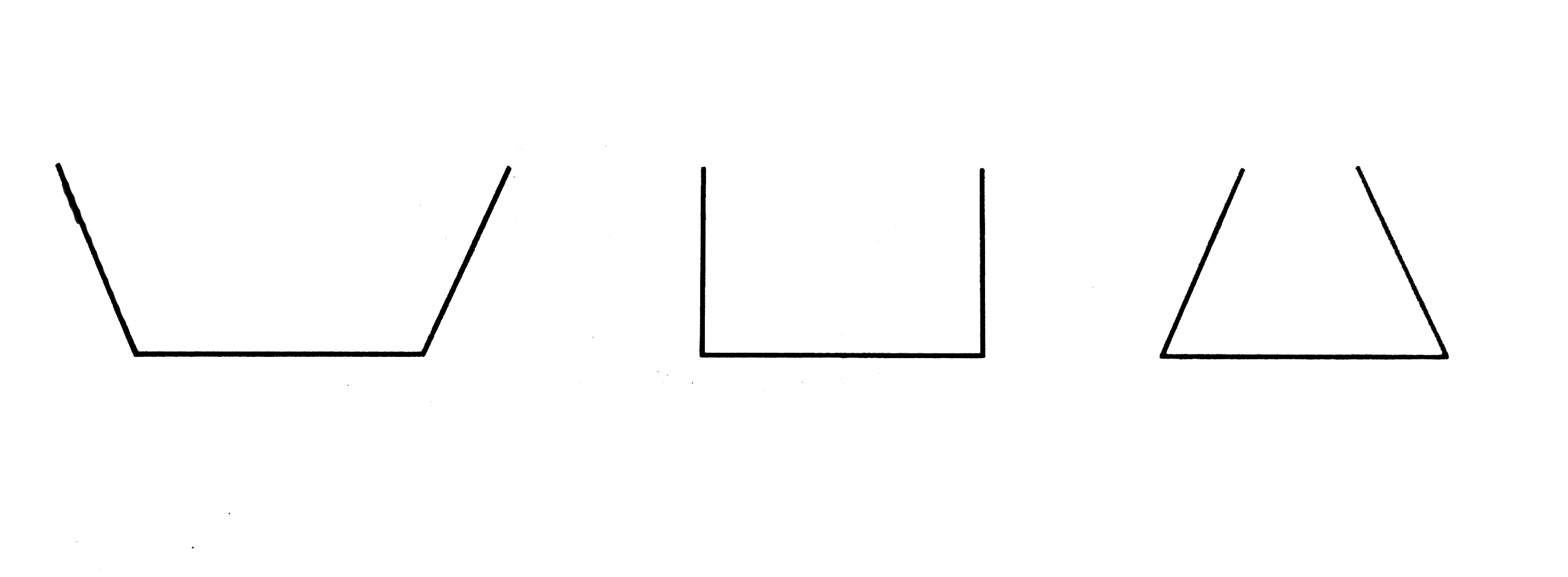
View SolutionThe three vessels shown in figure have same base area. Equal volumes of a liquid are poured in the thre vessels. The force on the base will be
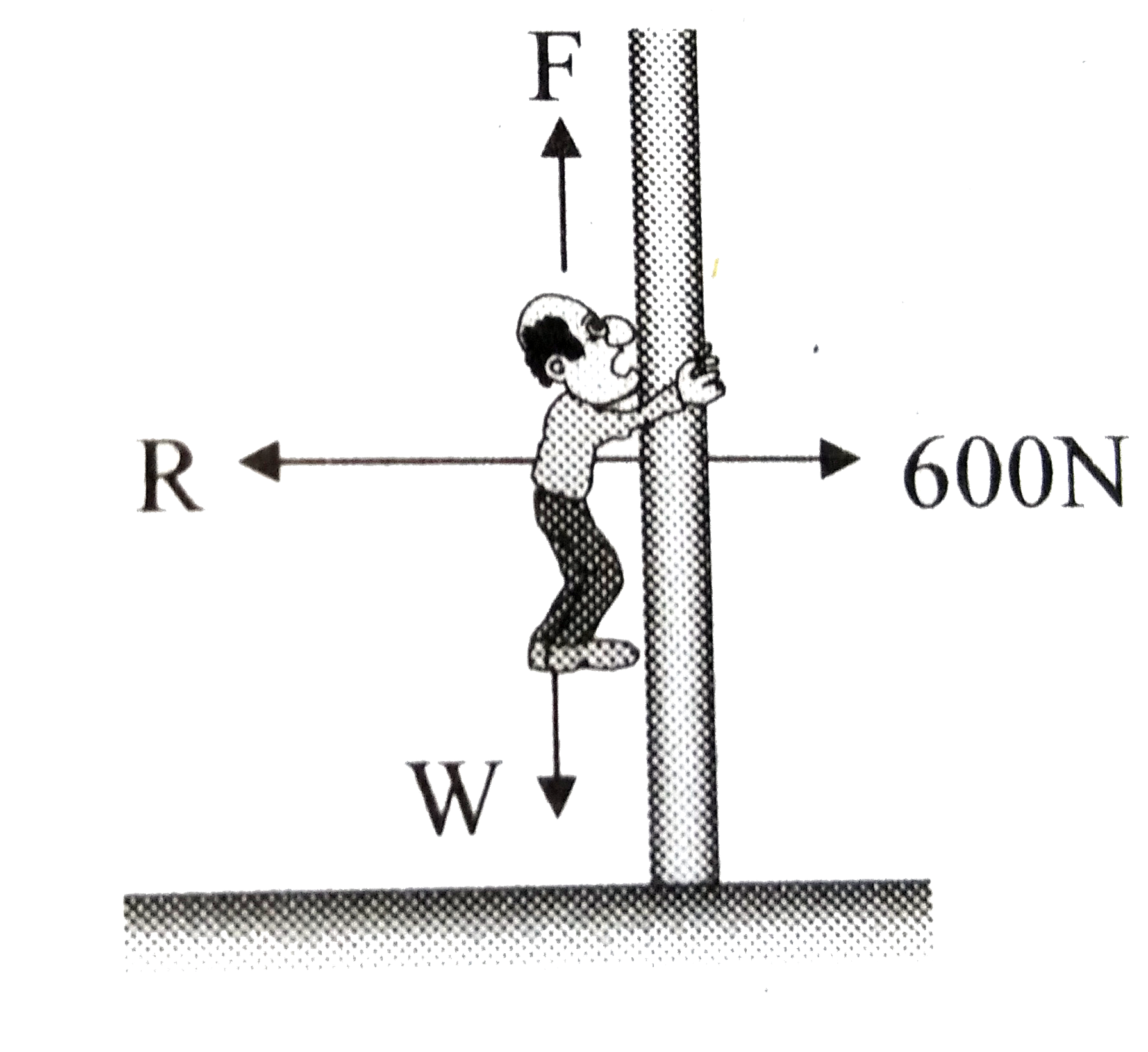
View SolutionA fireman of mass 60 kg slides down a pole. As shown in figure. He is pressing the pole with a force of 600 N. The coefficient of friction between the hands and the pole is `0.5.` With wht acceleration will the fireman slide down `(g=10 m//s^(2))`
View SolutionA tank is filled with water up to a height `H`. Water is allowed to come out of a hole `P` in one of the walls at a depth `D` below the surface of water. Express the horizontal distance `x` in terms of `H` and `D`
 .
.
View SolutionA point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals `mu`. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction `mu` and the distance x `(=QR)`, are, respectively close to:

View SolutionA 60 kg weight is dragged on a horizontal surface by a rope upto 2 metres. If coefficient of friction is `mu=0.5` the angle of rope with the surface is `60^(@)`and `g=9.8m//sec^(2),` then work done is
View SolutionWhen a body is moving on a surface, the force of friction is called
View SolutionThe speed of the wind passing over the wings of a small aeroplane is 70 m/s and below the wing is 60 m/s. If the mass of the plane is 1000 kg and the area of wing is `14 m^(2),` then what will be ther net vertical force on the aeroplane ?
? (Density of air `=1.2 kg//m^(3) and g=10 m//s^(2))`
View SolutionA rectangular vessel when full of water takes 10 minutes to be emptied through an orifice in its bottom. How much time will it take to be emptied when half filled with water
View SolutionA vessel completely filled with water has holes 'A' and 'B' at depths 'h' and '3h' from the top respectively. Hole 'A' is a square of side 'L' and 'B' is circle of radius 'r'. The water flowing out per second from both the holes is same. Then 'L' is equal to
View SolutionA large open tank has two holes in the wall. One is a square hole of side L at a depth y from the top and the other is a circular hole of radius R at a depth 4y from the top. When the tank is completely filled with water, the quantities of water flowing out per second from both holes are the same. Then, R is equal to
View SolutionA body of mass 2 kg is being dragged with uniform velocity of 2 m / s on a rough horizontal plane. The coefficient of friction between the body and the surface is 0.20. The amount of heat generated in 5 sec is
. `(4.2"joule"//cal and g=9.8 m//s^(2))`

View SolutionA spherical solild of volume V is made of a material of density `rho_(1)`. It is falling through a liquid of density `rho_(2)(rho_(2) lt rho_(1))`. Assume that the liquid applies a viscous froce on the ball that is proportional ti the its speed v, i.e., `F_(viscous)=-kv^(2)(kgt0)`. The terminal speed of the ball is
View SolutionThe heart of a man pumps 5 liters of blood through the arteries per minute at a pressure of 150 mm of mercury. If the density of mercury be `13.6xx10^(3) kg//m^(3)` and `g=10 m//s^(2)` then the power of heat in watt is :
View Solution
MCQ (COMPETITIVE THINKING) questions and complete solutions for chapter FRICTION IS SOLIDS AND LIQUIDS of TARGET PHYSICS (MARATHI ENGLISH) of Class 11