Complete Solutions to EXERCISE of chapter MODEL QUESTION PAPERS-SET 12 of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MODEL QUESTION PAPERS-SET 12 |
| UNITED BOOK HOUSE | EXERCISE |
| Number Of Questions | 49 |
| Academic Year | 2023-24 |
Which of the following sets have only one subset
View SolutionThe value of `1+i^2+i^4+i^6+....+i^16`is
View SolutionNo of diagonals of a 12 sided polygon are
View SolutionIf the sum of theree cosecutive numbers of an AP is 45, then the middle number will be
View SolutionThe acute angle between the two lines' 7x - 4y = 0 and 3x -11y = 2 will be
View SolutionThe circle `x^2+y^2-2x-2y+k=0`represents a point circle when k.=
View SolutionThe value of `lim_(xrarr3)(sqrt(x+3)+sqrt(x-3))/x`is
View SolutionIf f(x)=`2x^3-3x^2+4x-2`,then the value of `f'(3)` is
View SolutionTwo dice are thrown at a time.The probability that the sum of two numbers is equal to 5 is
View SolutionThe median of 1st 2013 natural number is
View SolutionFor any two sets A and B, if `A cupB` = `A cap B`, then show that A = B.
View SolutionA = {1, 2, 3, 4, 5}, B = {1, 3, 4} and the relation R from set A to set B where `(x, y) in R` implies x > y. Find the ordered pairs of `R^(-1)`
View SolutionShow that `tan67^@-tan22^@-tan67^@tan22^@=1`
View SolutionIn `/_\ABC`, if `angleC = 90^@`,. then find the value of tan A + tan B.
View SolutionIf ^nP_r=120 ^nC_(n-r) , find the value of r.
View Solutionx.and y are- real and if x + iy.=`5/(-3+4i)`,find the value of x and y.
View SolutionFind the constant term of the expansion of `(a^3-1/a^2)^15`
View SolutionIf the P th term of an AP is (3P - 5), then find the common difference and 15th term of this AP.
View SolutionFind the equation of a straight fine passes through the middle ofthe straight lines 2x - 3y + 1 =0 and 2x- 7= 3y.
View SolutionFind the ratio in which the plane xy divides the join of A(2, 3. 5) and B(-2, -5, -3).
View SolutionIf `y=xe^x`,show that xdy/dx=(1+x)y.
View Solution`f(x)=x^2+ax`,when ` 0lexle1` and `f(x)=3-bx^2`,when `1lexle2` if `limxrarr1f(x)=4`,then find the value of a and b.
View SolutionA unbiased coin tossed three times. Find the probability of getting 1 head
View SolutionIf the variance of a distribution is 4 coefficient of variation is 5%,then mean of the distribution is ___
View SolutionFor any two sets, show that `(A cap B) cup (A - B)= A`.
View SolutionIf `tan^2 alpha `= `1 + 2 tan^2 beta`, show that `cos2 beta` = `1 + 2cos 2alpha`.
View SolutionSolve :sin x 4 cos x = sin 2x 4 cos 2x.
View SolutionProve by mathematical induction, `1+1/4+1/9+...+1/n^2<2-1/n`when` n ge 2`, is a integer.
View SolutionIf arg `((z-1)/(z+1))=pi/4`,, then show that in complex plane, the locus of z is a cricle.
View SolutionFind the term independent of x of the expansion of `(1+x)^3(x-1/x)^6`
View SolutionIf pth, qth and rth terms of on AP are a. b and c, then show that a(q - r) + b(r - p) + c(p - q) = 0.
View SolutionA straight line form a right angled triangle with the axes. If the length of hypotenus and area of this triangle are 13 unit and 30 sq unit, find the equation of this straight line.
View SolutionIf the co-ordinate of vertices of a triangle are (10, 4), (-4, 9) and (-2, -1). Find the the co-ordinate of its ortho centre.
View SolutionFind the co-ordinate of a point on the circle ` x^2 +y^2 - 4x + 2y - 20 = 0` nearest to `(2, 3/2)`.
View SolutionThe co-ordinate of the vertices of a triangle are A(0, 2, -3), B(- 2, 0, -4) and C(3, 6, -3). Find the ratio in which the bisector of `angleBAC` divides BC and also find the co-ordinate of that point
View SolutionDifferentiate `x+1/x(x!=0)`at x = 1, with respect to x, with the help of 1st principle
View SolutionEvaluate : `lim_(xrarr0)sin(x^2+4x)/(x^3-5x^2+2x)`
View Solution‘If p' and q are rational numbers, then pq is also rational convert this compound statement into a simple statement and check whether the statement is true of false.
View Solution‘Square of a whole number is positive or negative’-find the validity of this compound statement.
View SolutionIf two numbers a and b are-chosen at random from the 1st 30 natural numbers, find the probability that the expresion `(a^2 -b^2) `is divisible by 3.
View SolutionFind A.M. and SD of the following distribution table :
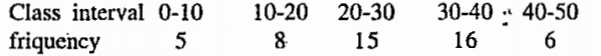
View SolutionUsing vector method in a triangle , prove that,
(i) `a/(sinA)=b/(sinB)=c/(sinC)` and
View SolutionIf `alpha`,`beta` positive acute angles and `sec(alpha+beta)-sec(alpha-beta)=2 cosec alpha` show that `sinalpha=cos (beta/2)-sin(beta/2)`
View SolutionDraw the graph and find the common region of the system of following inequations : `x + y le5`,` 2x - 3y ge6`, `x ge2`.
View Solutionif `z_1=1+isqrt3`,`z_2=sqrt3-i`show that (a)arg `(z_1z_2)=arg(z_1)+arg(z_2)`and (b) `arg(z_1//z_2)=arg(z_1)-arg(z_2)`
View SolutionFind the vlaue of `47 C_4+sum_(r=0)^ 3( 50-^ rC_3)`
View SolutionFind the length of the normal chord of a parabola `y^2 = 4x`, which makes an angle `45^@` with its axes.
View SolutionIf `theta` and `phi` are the eccentric angles of the end points of a chord which passes through the focus .of an ellipse`x^2/a^2+y^2/b^2=1`.Show that `tan(0//2)tan(phi//2)=((e-1)/(e+1))`,where e is the eccentricity of the ellipse.
View SolutionFind the equation of a hyperbola, having foci `(+- 7. 0)` and its eccentricity is `4//3`.
View Solution
EXERCISE questions and complete solutions for chapter MODEL QUESTION PAPERS-SET 12 of UNITED BOOK HOUSE of Class 11