Complete Solutions to EXERCISE of chapter MODEL QUESTION PAPERS-SET 3 of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MODEL QUESTION PAPERS-SET 3 |
| UNITED BOOK HOUSE | EXERCISE |
| Number Of Questions | 48 |
| Academic Year | 2023-24 |
If. b sin` beta` =` a sin (2alpha +beta)` then the.value of `cot(alpha+beta)/cotalpha`
View Solution`5^(2n+1)+3^(4n+2) (n in N)`is divisible by
View SolutionIf P, 2P + 2, 3P + 3 are in G.P. the 4th term Will be
View SolutionIf `((1-i)/(1+i))^r`is always real then the least value of r is
View SolutionThe straight line 3x+y=9 divides the straight line segment joining the points (1, 3) and (2, 7) are in ratio
View SolutionIf the point`P(at^2,2at)` is a end point of a chord of the parabola`y^2=4ax`which is passes through the focus, then the length of the chord is
View SolutionThe value of`lim_(xrarrpi)sinx/(x-pi)`is
View SolutionIf` y=sinxsinalpha,then dy/dx=`
View SolutionThe median of 22,20, 22, 25, 19, 30, 27 is
View Solutionvariance of 1st n natural number is
View Solution`(A^c cup A)^c=phi` is the relation true of false? Give reason.
View SolutionIf the realtion R defined as the set S = {1.-2, 3, 4},,`AA,a,b in s,aRb,`if and- only if b is the double of a. Find the set R.
View SolutionShow that` sectheta+tantheta=tan(pi/4+theta/2)`
View SolutionIn `/_\ABC`, if a = 3. b = 5 and c =7, show that the triangle is obtused.
View SolutionIf `| z + 2 | + | z - 2 | le 6`, find the maximum value of I z I.
View SolutionIf m=``^nC_2`show that ``^mC_2=3^(n+1)C_4`
View SolutionIf a+b=3,then show that the minimum value of |a+ib|=is `3/sqrt2`
View SolutionFind the sum of the following infinite G.P series 0.9+0.81+0.792+….
View SolutionShow that the distance between (1,-1) and `((2m^2)/(1+m^2),(1-m)^2/(1+m^2))`is not depend on m
View SolutionFind the radius of sphere passing through (2,0,1) and having centre(0,-4,1).
View SolutionProve that `lim_(xrarroo)(1+1/x)^x=e`
View SolutionFor all real values of x and y, if f(x+y)=f(x)f(y), f(5)=4, f'(0)=2, find f'(5).
View SolutionIfP(A)=1/2,P(B)=1/3)and `P(A capB)=1/4`find `(A 'capB')`
View SolutionIn.an examination. 50%of the condidates have passed in mathematics 50% have passed in physics, while 41% have passed in both the subjects. Find the total number of candidates if..41 of them have failed in both subjects. (By., using set theory).
View SolutionIf A,B,(A - B)are positive acute angles, then prove that geometrically : cos (A - B) = cos A cos B + sin A sin B
View SolutionShow that`cos((2pi)/7)+cos((4pi)/7)+cos((6pi)/7)=-1/2`
View SolutionShow that `a^6+a^4+a^2+1=0`,when `a=1/sqrt2(1+i)`
View SolutionProve by mathematical induction:`(3^(4n+1)+2^(2n+2))`is divisible by 7.
View SolutionShow that the co-efficient of the middle term of the expansion of`(1+x)^12`is equal to the sum of the co-efficient of middle terms of.'the expansion of `(1 + x)^11`.
View SolutionIf `(y/z)^a.(z/x)^b.(x/y)^c=1`and a,b,c are in A.P ,show that x,y,z are in G.P.
View SolutionIn `/_\XYZ`the equation of the perpendicularbisector of XY and XZ arc x-y + 5 = 0 and x + 2y= 0, If the coordinate of x is (1.-2),■ then find the equation of YZ.
View SolutionFind the distance of the point (3. 5) from the line 2x + 3y = 14measured parallel to th line x - 2y= 1,
View SolutionThe end’ points of a rod having length l are moving a long with two straight line which are perpendicular toeach othcr. Find the equation -of the locus of the point which divides the rod are in ratio 2:1.
View SolutionFind the equation of a circle .which passes through (-2. 1) and touches the straight line 3x - 2y= 6 at (4. 3).
View SolutionEvaluate:`lim_(x-0)((e^x-1)log_5(1+5x))/(sin^2x)`
View SolutionDifferentiate `a^x` with respect to x (a> 0) with the help 1st principle.
View Solution‘I80 is the multiple of 4 or 5 examine the validity of the compound statement.
View Solution‘x is such a real number that `4x^3 + 3x= 0`, then `x = O`’. Find the truth value of this compound statement by the method of contra-diction.
View SolutionThe AM and SD of the marks obtained in the subjects' Bengali, .English and History of 50 students',in a class are given below
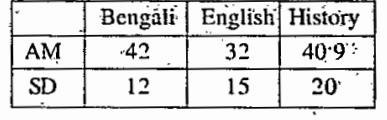 Find the maximum and minimum variability of the subjects with respect to obtained marks.-
Find the maximum and minimum variability of the subjects with respect to obtained marks.-
View SolutionIf `cosalpha=siny/sinx`,`cosbeta=sinz/sinx`and `cos(alpha-beta)=siny sinz`.Show that `tan^2x=tan^2y+tan^2z`
View SolutionSolve :`16^(sin^2x)+16^(cos^2x)=10.[0lexlepi]`
View SolutionFind the common solution region by. the graphical method.`3x+2yle18`,`x+2yle10`,`xge0`,`yge0`
View SolutionSolve :`x^2+x/sqrt2+1=0`
View SolutionFind the sum upto nth term : ,1 + 4 + 13 .+ 40 + ........
View SolutionFind the rank of the word MOTHER when its letters are arranged as in a dictionary
View SolutionAn equilateral triangle inscribe a parabola `y^2 = 4ax`. such that oneof the vertex of the triangle lies on the vertex of the parabola-. Find the,length of,the each side. of the triangle:
View SolutionIf the ellipse`x^2/a^2+y^2/b^2=1`passes through the intersecting points of two straight lines 7x + 13y -87=0 and 5x -8y + 7 = 0 and the'length of its latus rectum is`(32sqrt2)/5`then find the value of a and b and also find its eccentricity
View SolutionPQ is the double ordinate of the hyperbola `x^2/a^2-y^2/b^2=1` and O is the centre of the hyperbola. If triangle OPQ is an equilateral triangle, then show that the eccentricity of this hyperbola is e) `e^2 >4/3`
View Solution
EXERCISE questions and complete solutions for chapter MODEL QUESTION PAPERS-SET 3 of UNITED BOOK HOUSE of Class 11