Complete Solutions to QUESTIONBANK of chapter RELATIONS AND FUNCTIONS of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | RELATIONS AND FUNCTIONS |
| V PUBLICATION | QUESTIONBANK |
| Number Of Questions | 79 |
| Academic Year | 2023-24 |
If `(x+1, y-2)=(3,1)`, find the values of `x` and `y .`
View SolutionIf `P={a, b, c}` and `Q={r)`, form the séts `P xx Q` and `Q xx P .` Are these two products equal?
View SolutionLet `A={1,2,3}`,`B={3,4}` and `C={4,5,6}`.
Find
`Axx(BnnnC)`
View SolutionLet `P={1,2}`.Find `PxxPxxP`
View SolutionIf `R` is the set of all real numbers, what do the cartesian products `R xx R` and `R xx R xx R` represent?
View SolutionIf `(x/3+1,y-2/3)=(5/3,1/3)`, find the values
of x and y.
View SolutionIf `A xx B={(p, q),(p, r),(m, q),(m, r)}`, fịnd `A` and `B`
View SolutionIf the set A has 3 elements and the set B = {3,4,5}, then find the number of elements in `(A xx B)`.
View SolutionIf G = {7,8} and H ={5,4,2}, find `Gxx H` and `H xx G`
View SolutionState whether each of the following statetments is true or false. If the statement is false, rewrite the given statement correctly. If P = {m,n} and Q = {n,m}, then `P xx Q` ={(m,n),(n,m)}
View SolutionIf A = { - 1, 1}, find `A xx A xx A`.
View SolutionIf `A xx B`={(a,x), (a,y),(b,x),(b,y)} Find A and B
View SolutionLet `A={1,2}`,`B={1,2,3,4}`,`C={5,6}` and
`D={5,6,7,8}`.Verify that
`Axx(BnnnC)=(AxxB)nnn(AxxC)`
View SolutionLet A = {1,2} and B = {3,4}. Write `A xx B`. How many subsets will `A xx B` have? List them.
View SolutionLet A and B are two sets such that n (A) = 3 and n (B) = 2. If (x,1), (y,2),(z,1) are in `A xx B`, find A and B, where x,y and z are distinct elements.
View SolutionThe Cartesian product `A xx A` has 9 elements among which are found (-1,0) and (0,1). Find the set A and the remaining elements of `A xx A`
View SolutionLet `A={1,2,3,4,5,6}` be a set. Defined a relation R from A to A by `R={(x,y)//y=x+1}`
Represent the relation R using an arrow diagram.
View Solution`A={1,2,3,……,14}`. R is a relation from A to A defined by `R={(x,y): 3x-y = 0,x,y in A}`. Write the domain, range,co-domain of ,R.
View SolutionA relation R on set natural numbers is defined by `R={(x,y):y=x+5`,x is a natural number less than 4, `x, y in N`}
Write the relation in roster form.
View SolutionA = {1,2,3,5} and B = {4,6,9}. Define a relation R from A to B by R = {(x,y): the difference between x and y is odd: ` x in A, y in B}`. Write R in roster from.
View SolutionShows a relationship between the sets P and Q. write this relation roster from. What is its domain and range ?

View SolutionLet `A={1,2,3,4,6}`.Let R be the relation on
A defined by `R={(a,b):a,b in A, b` is
exactly divisible by a}
Find the domain of R.
View SolutionDetermine the domain and range of the
relation R defined by
`R={(x,x+5): x in {0,1,2,3,4,5}}`
View SolutionWrite the relation `R={(x,x^3): x` is a prime
number less than 10} in roster form.
View SolutionLet A = {x,y,z) and B = {1,2}. Find the number of relations from A to B
View SolutionLet R be the relation on Z defined by R = { ( a,b): a,b `in` Z, a - b is an integer}. Find the domain and range of R
View SolutionLet `N` be the set of natural numbers and the relation'R be defined on `N` such that `R={(x, y): y=2 x, x, doty in N}` What, is the domain, codomain and range of R? Is this relation a function?
View SolutionExamine each of the following relations given below and state in each case, giving reasons whether it is a function or not?
i) `R={(2,1),(3,1),(4,2)}`
ii) `R={(2,2),(2,4),(3,3),(4,4)}`
iii) `R={(1,2) ,(2,3),(3,4),(4,5),(5,6),(6,7)}`
View SolutionLe't `N` be the set of natural numbers. A real valued function is defined as `f:N→N` by `f(x)=2 x+1`. Using this definition, complete the table given below:
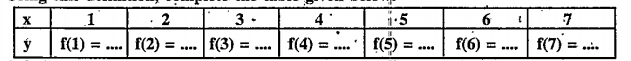
View SolutionDraw the graph of the function `f: R rarr R` defined by `f(x)=x^3, x in R`.
View SolutionLet `f(x)=x^2` and `g(x)=2x+1` be two
functions defined over the set of non-
negative real numbers. Find `(f+g)(x)`, `(f-g)(x)`,`(fg)(x)` and `(f/g)(x)`
View SolutionLet `f(x)=sqrtx` and `g(x)=x` be two
functions defined over the set of non-
negative real numbers. Find `(f+g)(x)`, `(f-g)(x)`,`(fg)(x)` and `(f/g)(x)`
View SolutionWhich of the following relations are functions ? Give reasons. If it is a functions determine its domain and range.{(2,1),(5,1),(8,1),(1,1),(14,1),(17,1)}
View SolutionFind the domain and range of the following functions.
`f(x)=-abs[x]`
View SolutionA function f is defined as `f(x)=2x-5`.
Write down the values of `f(0)`,`f(7)`,`f(-3)`.
View SolutionThe function 't' which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by `t (C ) = (9C)/5 +32`. Find t (0)
View SolutionFind the range of the following functions.
`f(x)=2-3x`,`x in R`,`x>0`
View SolutionLet `R` be the set of real numbers. Define the real function. f: `R rarr R` by `f(x)=x+1 0` and sketch the graph of this function.
View SolutionLet `R` be `a`.relation from `Q` to `Q` defined by `R={(a, b): a, b in Q` and `a-b in Z }.` Show that
i) `(a, a) in R` for all `a in Q`
ii) `(a, b) in R` implies that `(b, a) in R`
iii) `(a, b) in R` and `(b, c) in R` implies that `(a, c) in R .`
View SolutionLet f={(1,1),(2,3),(0,-1),(-1,-3)} be a linear function from `Z` into `Z`. Find `f(x)`.
View SolutionFind the domain of the function
`f(x)=(x^2+3x+5)/(x^2-5x+4)`
View SolutionThe function f is defined by
`f(x)={(2-x,,x,<,0),(2,,x,=,0),(2+x,,x,>,0):}`
Draw the graph of Find `f(x)`
View SolutionThe relation f is defined by `f (x) = {(x^2, 0 le x le 3)/(3x, 3 le x le 10)`
The relation g is defined by` g (x) = {(x^2,0 le x le 2)/(3x, 2 le x le 10)`
show that f is a function and g is not a function
View SolutionIf `f(x)=x^2`, find `(f(1.1)-f(1))/((1.1-1))`
View SolutionFind the domain of the following.
`f(x)=(x^2+2x+1)/(x^2-8x+12)`
View SolutionFind the domain and range of the following
functions.
`f(x)=sqrt(x-1)`
View SolutionFind the domain and range of the following functions.
`f(x)=abs[x-1]`
View SolutionLet `f={(x,x^2/(1+x^2)),x in R}` be a real
function from R to R. Determine the domain
and range of f.
View SolutionLet f,g: R `rarr` R be defined, respectively by `f (x) = x + 1,g (x) = 2x -3`. find `f + g,f - g` and `f/g`
View SolutionLet f = {(1,1), (2,3),(0, -1), (- 1, - 3)} be a function from Z to Z defined by `f (x) = ax + b`, for some integers a,b. determine a,b.
View SolutionLet R be a relation from N to N defined by R = `{(a,b) in N and a = b^2}`. Are the following true? `{(a,a) in R`, for all `a in N`}
View SolutionLet A = {1,2,3,4}, B = {1,5,9,11,15,16} and f = {(1,5),(2,9),(3,1),(4,5),(2,11),}. Are the following true? F is a function from A to B. Justify your answer.
View SolutionLet f be the subset of `Z xx Z` defined by `f = {(ab, a + b) : a,b in Z}` is f a function from Z to Z? justify your answer.
View SolutionLet A = {9,10,11,12,13} and let f : A `rarr` N be defined by f (n) = the highest prime factor of n. find the range of f.
View SolutionA relation `R` is defined on the set `Z` of integers as follows.`R ={ (x, y) in R: x^2+y^2=2 5}` Express `R` and `R^-1` as the sets of ordèred pairs and hence find their respective domains.
View SolutionLet `A={1 ,2,3,4,5}` and `B={1,2,3, ... ., 6,7} .` If `R` be a relation from `A` to the set B defined by
i) is square root of
ii) is cube root of, find `R` and also its domain and range.
View SolutionFind the domain and range of the function `f = {(x, (x^2 -1)/(x - 1)): x in R, x ne 1}`
View SolutionLet `R` be the relation on the set `Z` of all integers defined by `R={(x, y) : x,y in Z,x-y` is divisible by n}.Prove that
i) `(x, x) in R` for all `x in , Z`
ii) `(x, y) in R` implies that `(y, x) in R` for all `x, y in Z`
iii) `(x, y) in R` and `(y, z) in R` implies that `(x, z) in R` for all `x, y, z in Z`
View SolutionLet f be defined by `f(x)=x-4` and `g` be defined by `g(x)=(x^2-16)/(x+4), x ne-4.`
find `lambda` such that `f(x)=g(x)` for all `x`
View SolutionIf `f` is a real function defined by `f(x)=(x-1)/(x+1)`, then prove that `f(2 x)=(3f(x)+1)/(f(x)+3)`.
View SolutionFind the domain and range of the following functions:
i)`f(x)=1/(sqrt(x-5))`
ii) `f(x)=x/(1+x^2)`.
View SolutionLet f and `g` be two real functions defined by `f(x)=1/(x+4)` and `g(x)=(x+4)^3`, find the following:
i) `f-g`
ii) `f/g
` iii) 2f
View SolutionWhich of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
i) `{(2,1),(5,1),(8,1),(11,1),(14,1),(17,1)}`
ii) {`(2,1,(4,2),(6,3),(8,4),(10,5),(12,6),(14,7)}`
iii)`{(0,0),(1,1),(1,-1),(4,2),(4,-2),(9,3)(9,-3),(16,-4),
(16,-4)}`
iv) `{(1, 2),(1,3),(2,5)}`
v) `{(2,1),(3,1),(5,2)}`
vi) {`(1,2),(2,2),(3,2)}`
View SolutionIf `f(x)=x^2+x-1` and `g(x)=4 x-7`. be real functions then find:
i) `(f+g)(2)`
ii) `(f-g)(7)`
(iii) `(fg) (- 5 )`
iv) `(f/g)(4)`
View SolutionLet `f` and `g` be real functions defined by `f(x)=sqrt(x+4), x ge-4` and `g(x)=sqrt(x-4), x ge 4 .` Find the functions `f+g, f-g, f g, f/g`
View SolutionIf `af(x)+bf (1/x)=1/x-5` for `x ne 0`, where `a ne b`. Find `f(x)`
View SolutionIf `A={3,4,6} , B={1,3}` and `C={1,2,6}`, then find
(i) `A xx(B nn C)`
(ii) `B xx(A uu C)`
(iii) `(A-B) xx(A-C)`
View SolutionLet A and B are two sets such that n (A) = 3 and n (B) = 2. If (x,1), (y,2),(z,1) are in `A xx B`, find A and B, where x,y and z are distinct elements.
View SolutionLet `A` be a non - empty set such that `A xx B=A xx C` show that `B=C`
View SolutionLet `A subset B, C subset D`, then prove that `A xx C subset B xx D`
View SolutionLet `R` be the relation on `Z` defined by `R={(a, b), a, b in Z, a^2=b^2}` Find (i) `R` (ii) domain of `R` (iii) range of `R`
View SolutionLet R be the relation on Z defined by R = { ( a,b): a,b `in` Z, a - b is an integer}. Find the domain and range of R
View SolutionIf `f :R rarr R` is defined by `f(x)=x^2-3 x+2`, find `f(f(x))`. Also evaluate `f(f(5))`
View SolutionIf `f(x)=x+1/x` show that `(f(x))^3=f(x^3)+3 f(x)`
View SolutionFind the domain of the following.
`f(x)=(x^2+2x+1)/(x^2-8x+12)`
View SolutionDraw the graph of the real function `y=x^2+2 x+3`
View SolutionDraw the graph of the real function `y={[ x, if x le 0], [ x^2, if 0 lt x le 2]:}`
View SolutionLet `f: R rarr R` be a function defined by `f(x)=x^2+[x]+|x|-7, x in R`. Find the valueof 'f' at the points `-3.4,-2,-1.7,0,0.8,1,4.3`
View SolutionLet `f, g: R rarr R` be functions defined respectively by `f(x)=x+1, g(x)=2 x-3` Find fg.
View Solution
QUESTIONBANK questions and complete solutions for chapter RELATIONS AND FUNCTIONS of V PUBLICATION of Class 11