Complete Solutions to QUESTION BANK of chapter PROBABILITY of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | PROBABILITY |
| V PUBLICATION | QUESTION BANK |
| Number Of Questions | 89 |
| Academic Year | 2023-24 |
Two coins (a one rupee coin and a two rupee coin) are tossed once. Find sample space.
View SolutionThe number of outcomes in the sample space of the random experiment of throwing two dice is....a)6^3
View SolutionIn each of the following experiments specify appropriate sample space
i) A boy has a 1 rupee coin, a 2 rupee coin and a 5 rupee coin in his pocket. He takes out two coins out of his pocket, one after the other.
ii) A person is noting down the number of accidents along a busy highway during a year.
View SolutionA coin is tossed. If it shows head, we draw a ball from a bag consisting of 3 blue and 4 white balls, if it shows tail we throw a die. Describe the sample space of this experiment.
View SolutionDescribe the sample space for the indicated experiment. A coin is tossed three times
View SolutionThe number of outcomes in the sample space of the random experiment
of throwing two dice is………
View SolutionDescribe the sample space.A coin is tossed four times
View SolutionDescribe the sample space for the following event:
A coin is tossed and a die is thrown.
View SolutionDescribe the sample space of the given experiment.
A coin is tossed and then a die is rolled only in case a head is shown on the coin.
View SolutionDescribe the sample space for the following event:
2 boys and 2girls are in a Room X and 1 boy and 3 girls in room Y. Specify the sample space for the experiment in which a room is selected and then a person.
View SolutionDescribe the sample space for the following event:
One die of red colour, one of white colour and one of blue colour are placed in a bag. One die is selected at random and rolled, its colour and the number on its upper most face is noted.
View SolutionAn experiment consists of recording boy-girl composition of families with 2 children.
i) What is the sample space if we are interested in knowing whether it is a boy or girl in the order of their births?.
ii) What is the sample space if wé are interested in the number of girls in the family?
View SolutionA box contains 1 red and 3 identical white balls. Two balls are drawn at random in succession without replacement. Write the sample-space for this experiment.
View SolutionDescribe the sample space for the following event:
An experiment consists of tossing a coin and then throwing it second time if a head occur. If a tail occurs on the first toss,then a die is rolled one.
View SolutionSuppose 3 bulbs are selected at randóm from a lot. Each bulb is tësted-and classified as defective (D) or non-defective (N): Write the,sample space of this experiment.
View SolutionDescribe the sample space for the following event:
A coin is tossed. If the outcome is a head, a die is thrown. If the die shows up an even number, the die is thrown again.
View SolutionThe number 1,2,3 and 4 are written separately on four slips of paper. The slips are put in a box and mixed thoroughly. A person draws two slips from the box, oné after the other, without replacemient. Describe the sample space for the experiment.
View SolutionAn experiment consists of rolling a die and then tossing a coin once if the number on the die is even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.
View SolutionA coin is tossed: If it shows a tail, we draw a ball from a box which contains 2 red and 3 black balls. If it shows head, we throw a die. Find the sample space for this experiment.
View SolutionA die is thrown repeatedly ụntil a six comes up. What is the sample space for this experiment?
View SolutionTwo dice are thrown and the sum of the numbers which come up on the dice is noted. Let us consider the following events associated with this experiment.
A : the sum is even .
B : the sum is a multiple of 3
C : the sum is less than 4.
D : the sum is greater than 11 Which pairs of these events are mutually exclusive?
View SolutionA coin is tossed three times, consider the following events.
A: No head apears,
B: Exactly one head appear
C: Atleast two heads appear.
Do they form a set of mutually exclusive and exhaustive events?
View SolutionA die is rolled. Let E be the event "die shows 4" and F be the event "die shows even number". are E and F mutually exclusive?
View SolutionA die is thrown. describe the following events:
A: a number less than 7.
View SolutionAn experiment involves rolling a pair of dice and recording the numbers that comeup. Describe the follơowing events.
A: the sum is greater than 8
B: 2 occurs on either
C : the sum is at least 7 and multiple of 3.
Which pairs of these events are mutually exclusive?
View SolutionThree coins are tośsed once. Let A denote the event "three heads show". B denote the event "two heads and one tail show", C denote the event "three tails show" and Đ denote the event "a head shows on the first coin".
Which events are (i) mutually exclusive? (ii) simple? (iii) compound.
View SolutionOne card is drawn from a well shuffled deck of 52 cards. If each outcome is equally Iikely, calculate the probability that the card will be i) a diamond.
ii) not an ace
iii) a black card (a club or, a spade)
iv) not a diamond
v) not a black card
View SolutionA bag contains 9 discs of which 4 are red, 3 are blue and 2 are yellow. The discs are similar in shape and size. A disc is drawn at random from the bag. Calculate the probability that it will be (i) red, (ii) yellow, (iii) blue, (iv) not blue, (v) either red or blue.
View SolutionTwo students, Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that both will not qualify the examination.
View SolutionA committee of two persons is selected from two men and two women. What is the probability that the committee will have one man?
View SolutionA coin is tossed twice,what is the probability that atleast one tail occurs?
View SolutionA die is rolled,find the probability of following event:
A prime number will appear.
View SolutionA card is selected from a pack of 52 cards a) How many points are there in the sample space? b) Calculate the probability that the card is an ace of spades. c) Calculate the probability, that the card is (i) an ace |(ii) black card
View SolutionA fair coin with 1 marked on one face and 6 on the other and a fair die are
both tossed.find the probability that the sum of numbers that turn up 12.
View SolutionThere are four men and six women on the city council.If one council member
is selected for a committee at random,how likely is it that it is a woman?
View SolutionA fair coin is tossed four times and a person win Re 1 for each head and lose Rs. '1.50' for each tail that turns up. From the sample space calculate how many different amounts of money you can have after four tosses and the probability of having each of these amounts.
View SolutionThree coins are tossed once. Find the probability of getting. (i) 3 heads
(ii) 2 heads
(iii) atleast 2 heads
(iv) atmost 2 heads
(v) no head
(vi) 3 tails
(vii) 'exactly two tails
(viii) no tail
(ix) atmost two tails.
View SolutionIf `2/11` is the probability of an event A,then what is the probability of the event 'not A'?
View SolutionA letter of the word `ASSASSINATION` are randomly chosen. Find the probability that letter is a consonant.
View SolutionIn a lottery, a' person choses six different natural numbers at random from 1 to 20, and if these six numbers match with the six numbers already fixed by' the lottery committè, he wins the prize. What is the próbability of winning the prize in the game?
View SolutionCheck whether the following probabilites P(A) and P(B) are consistently defined.
`P(A)=0.5,P(B)=0.4,P(AcupB)=0.8`
View SolutionFill in the blank space.
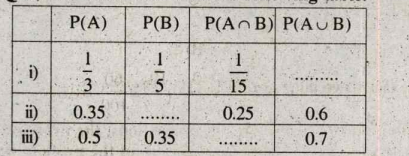
View SolutionGiven `P(A)=3/5` and `P(B)=1/5`
Find P(A or B), if A and B are mutually exclusive events.
View SolutionIf E and F are events such that `P(E)=1/4,P(F)=1/2`,and `p(E and F)=1/8`. find P(E or F).
View SolutionEvents E and F are such that P(not E or not F)=`0.25`, state whether `E` and `F` are mutually exclusive.
View SolutionIf A and B are two events such that `P(A)=0.42`,`P(B)=0.48` and `P(AbigcapB)=0.16` then, find: P(not B).
View SolutionIn class XI of a school 40% of the students study Mathematics and 30% study Biology, 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying mathematics or Biology.
View SolutionIn an entrance test that is graded on the basis of two examinations, the probability of a randomiy chosen student passing the first examination is `0.8` and the probability of passing the second examination is `0.7` . The probability of passing atleast one of them is `0.95` . What is the probability of passing both?
View SolutionThe probability that a student will pass the final examination. in both English and Hindi is '0.5' and the probability of passing neither is '0.1 .' If the probability of passing the English examination is '0.75', what is the probability of passing the Hindi examination. Let probability: of passing English be 'E' and probability of passing Hindibe 'H'.
View SolutionIn a class of 60 students, 30 opted for NCC, 32 opted for NSS and 24 opted for both NCC and NSS. If one of these students is selected at random, find:
The probability that the student opted for NCC and NSS.
View SolutionOn her vacations, Veena visits four cities (A, B, C and D ) in a random order. What is the probability that she visits i) A before B? ii) A before B and B before C? iii) A first and B last? iv) A either first or second? v) A just before B?
View SolutionFind the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards , it contains all kings
View SolutionIf `A,B,C` are three events assọciated with a random experiment, prove that
`P(AuuBuuC)`=`P(A)+P(B)+P(C)-P(AnnB)-P(AnnC)- P(BnnC)+`
` P(AnnBnnC)`
View SolutionIn a relay race there are-five teams 'A, B, C, D' and 'E'. a) What is the probability that 'A, B' and 'C' finish first, second and third, respectively. b) What is the probability that 'A, B' and 'C' 'are first three to finish (in any order) (Assume that all finishing orders are equally likely)
View SolutionA box contains 10 red marbles,20 blue marbles and 30 green marbles.
5 marbles are drawn from the box,what is the probability that all will
be blue.
View Solution4 cards are drawn from a well shuffled deck of 52 cards.What is the probability of obtaining 3 diamonds and one spade?
View SolutionA die has two faces each with number 1,three faces with number 2 and one face with number 3.If the die is rolled once,determine `P(1 or 3)`.
View SolutionIn a certain lottery ticket 10000 tickets are sold and 10 equal prizes are awarded.
What is the probability of not getting a prize,if you buy 10 tickets.
View SolutionOut of 100 students,two sections of 40 and 60 are formed.If you and your friend are among the 100 students,what is the probability that You both enter the same section?
View SolutionThree letters are dictated to three persons and an envelope is addressed to each of them, the letters, are inserted' into the envelopes at random so that each envelope contains exactly one letter. Find the probability that at least one letter is in its proper envelope.
View SolutionA and B are two events such that `P(A)=0.54`, `P(B)=0.69` and `P(A nn B)=0.35` Find (i) `P(A uu B)`. (ii) `P(A^(prime) nn B^(prime))` (iii) `P(A nn B^(prime))` (iv) `P(B nn A^(prime))`
View SolutionFrom the employees of a company, 5 persons are selected to represent them in the managing committee of the company. Particulars of five persons are as follows: A person is selected at random from this group to act as a spokesperson. What is the probability that the spokesperson will be either male or over 35 vears?
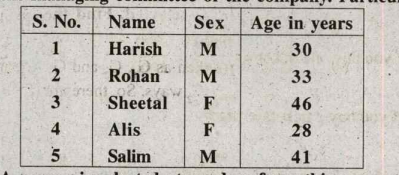
View SolutionThe number lock of a suitcase has 4 wheels, each labelled with ten digits from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the sequence to open the suit case?
View SolutionFrom a group of 2 boys and 3 girls, two childiren are selected. Find the sample space associated to this random experiment.
View SolutionA coin is tossed. If it shows head, we draw a ball from a bag consisting of 3 blue and 4 white balls, if it shows tail we throw a die. Describe the sample space of this experiment.
View SolutionAn experiment consists of rolling a die and then tossing a coin once if the number on the die is even. If the number on the die is odd, the coin is tossed twice. Write the sample space for this experiment.
View SolutionA coin is tossed repeatedly until a head comes up. Write the sample space.
View SolutionAn experiment involves rolling a pair of dice and recording the numbers that comeup. Describe the follơowing events.
A: the sum is greater than 8
B: 2 occurs on either
C : the sum is at least 7 and multiple of 3.
Which pairs of these events are mutually exclusive?
View SolutionFrom a group of 2 boys and 3 girls, two children are selected at random. Describe the events.
(i) A= both selected children are girls. (ii) B= the selected group consists of one boy and one girl. (iii) C= at least one boy is selected.
Which pair(s). of events is (are) mutually exclusive?
View SolutionTwo dice are thrown and the sum of the numbers which come up on the dice is noted. Let us consider the following events associated with this experiment.
A : the sum is even .
B : the sum is a multiple of 3
C : the sum is less than 4.
D : the sum is greater than 11 Which pairs of these events are mutually exclusive?
View SolutionFind the probability of gétting a head in a toss of an unbiased coin.
View SolutionIn a simultaneous toss of two coins,find the probability of getting: 2 heads.
View SolutionThree coins are tossed once. Find the probability of getting. (i) 3 heads
(ii) 2 heads
(iii) atleast 2 heads
(iv) atmost 2 heads
(v) no head
(vi) 3 tails
(vii) 'exactly two tails
(viii) no tail
(ix) atmost two tails.
View SolutionA die is thrown. Find the probability of getting (i) an even number (ii) a prime number. (iii) a number greatér than or equal to 3 (iv) a number Iess than or equal to 4 (v) a number more than 6 (vi) a number less, than or equal to 6 .
View SolutionFind the probability that a leap year should have 53 sundays.
View SolutionThree dice are thrown together. Find the probability of getting a total of atleast 6 .
View SolutionWhat is the probability that a nümber selected from the numbers `1,2,3...... 25` is a prime number, when each of the given numbers is equally likely to be selected?
View SolutionTickets numbered from 1 to 20 are mixed up together and then a ticket is drawn at random. What is the probability that the ticket has a number which is a multiple of `3` or `7` ?
View SolutionA coin is tossed. If head comes up, a die is thrown,but if tail comes up, the coin is tossed again. Find the probability of obtaining: (i) twỏ tails (ii) head and number 6 (iii) head and an even number
View SolutionOne card is drawn from a pack of 52 cards, each of the 52 cards being equally likely to be drawn. Find the probability that the card drawn is: (i) an ace, (ii) red, (iii) either red or king, (iv) red and a king.
View SolutionAn urn contains 9 red, 7 white and 4 black balls. If two balls are drawn at random, find the probability. that, (i) both the balls are red (ii) one ball is white, (iii) the balls are of the saime colour (iv) one is white and other red.
View SolutionIn a lottery of 50 tickets numbered from 1 to 50,two tickets are drawn
simultaneously.Find the probability that : Both the tickets
drawn have prime numbers.
View SolutionA word consists of 9 letters, 5 consonants and 4 vowels. Three letters are chosen at random. What is the probability that more than one vowel will be selected?
View SolutionA bag contains 50 tickets numbered '1,2,3, ....,50: of which, five are drawn at random and arranged in ascending order of magnitude `(x_1 lt x_2 lt x_3 lt x_4 lt x_5)` Find the probability that `x_3=30 `
View SolutionFour persons are to be chosen at random from a group of 3 men, 2 women and 4 children. Find the próbability of selecting:" (i) 1 man, 1 woman and 2 children (ii) exactly 2 children (iii) 2 women
View SolutionA box contains 10 bulbs, of which just three,are defective. If a random sample of five bulbs is drawn, find the probabilities that the sample contains: i) exactly one defective bulb
(ii)exactly two defective bulbs
(iii) no defective bulbs.
View SolutionFive marbles are drawn from a bag which contains 7 blue marbles and 4 black marbles. What is the probability that
(i) all will blue?
(ii) 3 will be blue and 2 black?
View SolutionFind the probability that when a hand of 7 cards is drawn from a well shuffled deck of 52 cards , it contains all kings
View SolutionIn a single throw of three dice, determine the probability of getting (i) a total of 5 .
(ii) a total of at most 5
(iii) a total of at least 5 .
View Solution
QUESTION BANK questions and complete solutions for chapter PROBABILITY of V PUBLICATION of Class 11