Complete Solutions to SOLVED PROBLEMS of chapter MATRICES of Class 11 book with complete answers and questions
| Class 11 | MATHS |
| Chapter | MATRICES |
| VIKRAM PUBLICATION ( ANDHRA PUBLICATION) | SOLVED PROBLEMS |
| Number Of Questions | 45 |
| Academic Year | 2023-24 |
If `A=[(2,3,-1),(7,8,5)]` and `B=[(1,0,1),(2,-4,-1)]` then find A+B.
View SolutionIf `[(x-1,2,y-5),(z,0,2),(1,-1,1+a)]=[(1-x,2,-y),(2,0,2),(1,-1,1)]` then find the values of x,y,z and a.
View SolutionFind the trace of A, if `A = [(1,2,-1//2),(0,-1, 2),(-1//2,2,1)]`
View SolutionIf `A=[(4,-5),(-2,3)]` then find `-5A`.
View SolutionFind the additive inverse of A where `A = [(i,0,1),(0,-i, 2),(-1,1,5)]`
View SolutionIf `A=[(2,3,1),(6,-1,5)]` and `B=[(1,2,-1),(0,-1,3)]` then find the matrix X, such that `A+B-X=0`. What is the order of the matrix X ?
View SolutionIF `A=[{:(0,1,2),(2,3,4),(4,5,6):}],B=[{:(1,-2,0),(0,1,-1),(-1,0,3):}]` then find A-B and 4B-3A.
View Solutionif `A=[{:(1,2),(3,4):}]`, `B=[{:(3,8),(7,2):}]` and 2X+A=B then find X
View SolutionTwo factories I and II produce three varieties of pens namely, Gel, Ball and Ink pens. The sale in namely, Gel, Ball and Ink pens by both the factories in the month of September and October in a year are given by the following matries A and B.
September sales (in Rupees)

October sales (in Rupees)
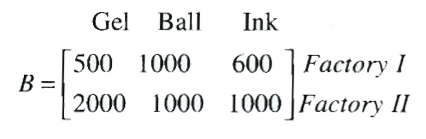
(i) Find the combined sales in September and October for each factory in each variety.
(ii) Find the decrease in sales from September to October.
View SolutionConstruct a `3 xx 2` matrix whose elements are defined by `a_(ij) = 1/2|i - 3j|`
View SolutionIf `A = [(0,1,2),(1,2,3),(2,3,4)], B = [(1,-2),(-1,0),(2,-1)]` then find AB and BA.
View SolutionIf `A=[(1,-2,3),(2,3,-1),(-3,1,2)]` and `B=[(1,0,2),(0,1,2),(1,2,0)]` then examine whether A and B commute with respect to multiplication of matrices.
View Solutionif `A = [(I,0)(0,-i)]` then show that `A^(2) = -1 (i^(2)=-1)`.
View SolutionIf `A = [(cos theta, sin theta),(-sin theta, cos theta)]` then show that for all the positive integers n, `A^(n) = [(cos n theta,sin n theta),(-sin n theta,cos n theta)]`.
View SolutionIF `A=[{:(1,2,2),(2,1,2),(2,2,1):}]` then show that `A^2-4A-5I=O`.
View SolutionIF `A=[{:(-2,1,0),(3,4,-5):}]` and `B=[{:(1,2),(4,3),(-1,5):}]` then find A+B'.
View SolutionIF `A=[{:(-1,2),(0,1):}]` then find AA'. Do A and A' commute with respect to mulitplication of matrices?
View SolutionIf `[(0,4,-2),(-4,0,8),(2,-8,x)]` is a skew symmetric matrix then find the value of x.
View SolutionFor any `n xx n` matrix A, prove that A can be uniquely expressed as a sum of a symmetric matrix and a skew symmetric matrix.
View SolutionShow that `|{:(1,a,a^2),(1,b,b^2),(1,c,c^2):}|=(a-b)(b-c)(c-a)`
View SolutionShow that `|{:(b+c,c+a,a+b),(c+a,a+b,b+c),(a+b,b+c,c+a):}|=2|{:(a,b,c),(b,c,a),(c,a,b):}|`
View SolutionShow that `|{:(1,a^2,a^3),(1,b^2,b^3),(1,c^2,c^3):}|` =(a-b)(b-c)(c-a)(ab+bc+ca)
View Solutionfind determinant of` |(1, omega, omega^(2)),(omega, omega^(2),1),(omega^(2),1,omega)|=`
View SolutionShow that `|{:(a-b-c," "2a," "2a),(" "2b,b-c-a," "2b),(" "2c," "2c,c-a-b):}|=(a+b+c)^(3)`
View SolutionShow that the determinant of skew - symmetric matrix of order three is always zero.
View SolutionFiind the valueof x if:
`|{:(x-2, 2x-3, 3x-4),(x-4, 2x-9, 3x-16),(x-8, 2x-27, 3x-64):}|=0`
View SolutionFind the Adjoint and Inverse of the matrix `A = [(1,2),(3,-5)]`
View SolutionFind the adjoint and the inverse of the matrix `A=[{:(1,3,3),(1,4,3),(1,3,4):}]`
View SolutionShow that the matrix `A=[{:(1,2,1),(3,2,3),(1,1,2):}]` is non-singular and find `A^-1`.
View SolutionFind the rank of `A=[{:(0,1,2),(1,2,3),(3,2,1):}]` using elementary transformations.
View SolutionFind the rank of `A=[{:(1,2,0,-1),(3,4,1,2),(-2,3,2,5):}]` using elementary transformations.
View SolutionApply the test of rank to examine whether the following equations are consistent.
`2x - y + 3z = 8, -x + 2y + z = 4,3x + y - 4z = 0` and, if consistent, find the complete solution.
View SolutionSolve the following system of equations by using Cramer,s ruel .
`3x+4y+5z=18,2x-y+8z=13,5x-2y+7z=20`
View SolutionSolve the equations `3x+4y+5z=18,2x+y+8z=13,5x-2y+7z=20` by matrix inversion method.
View SolutionSolve the following system of equations by using Cramer,s ruel .
`3x+4y+5z=18,2x-y+8z=13,5x-2y+7z=20`
View SolutionSolve the system of equations `2x+4y-z=0,x+2y+2z=5,3x+6y-7z=2` by Gauss Jordan Method.
View SolutionSolve the following- system of equations, `2x + 5y + 6z = 0, x - 3y + 8z = 0, 3x + y - 4z = 0`
View SolutionThe number of nontrivial solutions of the system: `x-y+z=0, x+2y=0, 2x+y+3z=0` is
View SolutionTheorem: Matrix multiplication is associative, i.e., if conformability is assured for the matrices A, B and.C, then (AB)C = A(BC).
View SolutionTheorem : Matrix multiplication, is distri-butive over matrix addition i.e.. If con-formability is assured for the matrices A, B .and C, then.
i) A(B + C) = AB + AC
ii) (B + C)A = BA + CA
View SolutionIf A is any matrix, then: `(A^(T))^(T) =A`
View SolutionIf A-and B are two matrices of same type, then `(A+B)^(T) =A^(T) + B^(T)`
View SolutionIf A and B are two matrices for which conformability for multiplication is assured, then prove`(AB)^(T) = B^(T)A^(T)`
View SolutionIf A is an invertible matrix and A is also invertible then prove `(A^(T))^(-1) = (A^(-1))`
View SolutionA certain book shop has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are Rs. 80, Rs. 60, Rs. 40 each respectively. Using matrix algebra, find the total value of the books in the shop.
View Solution
SOLVED PROBLEMS questions and complete solutions for chapter MATRICES of VIKRAM PUBLICATION ( ANDHRA PUBLICATION) of Class 11
All Exercises from VIKRAM PUBLICATION ( ANDHRA PUBLICATION) Class 11 MATHS MATRICES
- SOLVED PROBLEMS
- TEXTUAL EXERCISES (EXERCISE -3( c)
- TEXTUAL EXERCISES (EXERCISE -3( d)
- TEXTUAL EXERCISES (EXERCISE -3( e)
- TEXTUAL EXERCISES (EXERCISE -3( f)
- TEXTUAL EXERCISES (EXERCISE -3( g)
- TEXTUAL EXERCISES (EXERCISE -3( h))
- TEXTUAL EXERCISES (EXERCISE -3( i))
- TEXTUAL EXERCISES (EXERCISE -3(a))
- TEXTUAL EXERCISES (EXERCISE -3(b))