Complete Solutions to Section D - Chapter End Test of chapter ATOMIC PHYSICS of Class 12 book with complete answers and questions
| Class 12 | PHYSICS |
| Chapter | ATOMIC PHYSICS |
| A2Z | Section D - Chapter End Test |
| Number Of Questions | 30 |
| Academic Year | 2023-24 |
In hydrogen atom, when electron jupms from second to first orbit, then enrgy emitted is
View SolutionThe diagram shown the energy levels for an electron in a certain atom. Which transition shown respresents emissions of a photon with the most energy ?
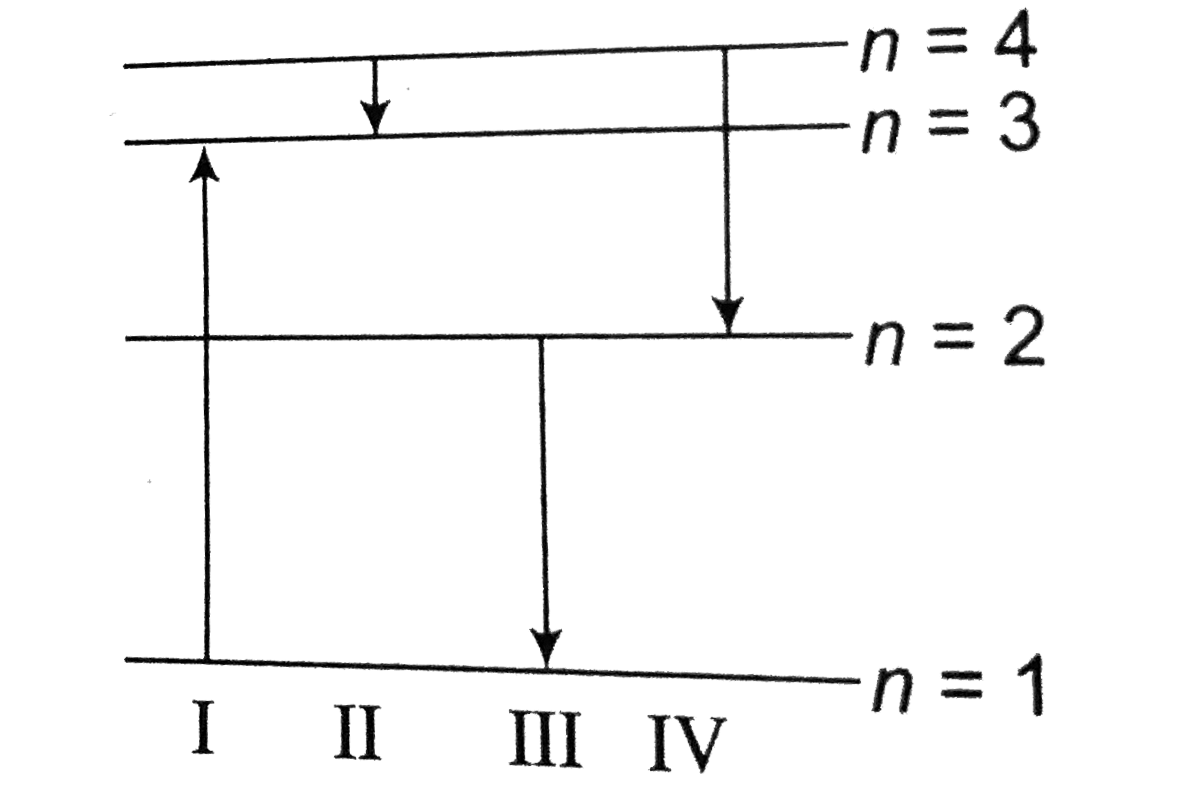
View SolutionAn energy of `24.6 eV` is required to remove one of that electrons from a neutal helium atom. The enegy (in `eV`)required to remove both the electrons from a netural helium atom is
View SolutionThe transition from the state `n = 4` to `n = 3` in a hydrogen-like atom results in ultraviolet radiation. Infared radiation will be obtained in the transition
View SolutionA hydrogen atom and a `Li^(2+)` ion are both in the second excited state. If `l_H` and `l_(Li)` are their respective electronic angular momenta, and `E_H and E_(Li)` their respective energies, then
(a) `l_H gt l_(Li) and |E_H| gt |E_(Li)|`
(b) `l_H = l_(Li) and |E_H| lt |E_(Li)|`
(C ) `l_H = l_(Li) and |E_H| gt |E_(Li)|`
(d) `l_H lt l_(Li) and |E_H| lt|E_(Li)|`
View SolutionThe electric potential between a proton and as electron is given by `V= V_(0) ln (r )/(r_(0))` , where`r_(0)` is a constant . Assuming Bohr's model to be applicable , write variation of `r_(n)` with `n,n` being the principal quantum number ?
View SolutionA hydrogen like atom with atomic number Z is in an excited state of quantum number 2n. It can emit a maximum energy photon of 204 eV. If it makes a transition ot quantum state n, a photon of energy 40.8 eV is emitted. Find n, Z and the ground state energy (in eV) of this atom. Also calculate the minimum energy (in eV) that can be emitted by this atom during de-excitation. Ground state energy of hydrogen atom is – 13. 6 eV.
View SolutionThe transition from the state `n = 4` to `n = 3` in a hydrogen-like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition
View SolutionIn a hypotherical Bohr hydrogen, the mass of the electron is doubled. The energy `E_(0)` and the radius `r_(0)` of the first orbit will be (`a_(0)` is the Bohr radius)
View SolutionWhat is the radius of iodine atom (at no. `53`, mass number `126`)?
View SolutionAn electron passing through a potential difference of `4.9 V` collides with a mercury atom and transfers it to the first excited state. What is the wavelength of a photon corresponding to the transition of the mercury atom to its normal state?
View SolutionWhich of the following atoms has the lowest ionization potential ?
View SolutionThe seond line of Balmer series has wavelength `4861 Å` The wavelength o fthe first line Balmer series is
View SolutionIf the wavelength of photon emitted due to transition of electron from third orbit to first orbit in a hydrogen atom is `lambda` then the wavelength of photon emitted due to transition of electron from fourth orbit to second orbit will be
View SolutionIf the series limit wavelength of the Lyman series for hydrogen atom is `912 Å`, then the series limit wavelength for the Balmer series for the hydrogen atom is
View SolutionThe first line of Balmer series has wavelength `6563 Å`. What will be the wavelength of the first member of Lyman series?
View SolutionAn atom makes a transition from a state of energy `E` to one of lower energy `E`. Which of the following gives the wavelength of the radiation emitted in terms of the Planck's constants `h` and the speed of light `c`?
View SolutionThe ratio of the speed of the electron in the first Bohr orbit of hydrogen and the speed of light is equal to (where `e, h` and `c` have their usual meanings)
View SolutionAn electron in `H` atom makes a transition from `n = 3` to `n = 1`. The recoil momentum of the `H` atom will be
View SolutionIf the atom`(_100)Fm^(257)` follows the Bohr model the radius of `_(100)Fm^(257)` is `n` time the Bohr radius , then find `n` .
View SolutionThe first excited state of hydrogen atom is `10.2 eV` above its ground state. The temperature is needed to excite hydrogen atoms to first excited level is
View SolutionThe electron in a hydrogen atom makes a transition from an excited state to the ground state. Which of the following statements is true?
View SolutionThe electron in a hydrogen atom makes a transition `n_(1) rarr n_(2)`, where `n_(1)` and `n_(2)` are the principle quantum numbers of the two states. Assume the Bohr model to be valid. The time period of the electron in the initial state is eight times that in the final state. the possible values of `n_(1)` and `n_(2)` are
View SolutionThe total energy of an electron in the ground state of hydrogen atom is `- 13.6 eV`. The potiential energy of an electron in the ground state of `Li ^(2+)` ion will be
View SolutionThe orbital velocity of electron in the ground state is `v`. If the electron is excited to enegry staet `- 0.54 eV` its orbital velocity will be
View SolutionIn hydrogen atom, the transition takes place from `n = 3` to `n = 2`. If Rydberg's constant is `1.09 xx 10` per metre, the wavelength of the limit emitted is
View SolutionThe wavelength of the first line of Balmer series is `6563 Å`. The Rydberg's constant is
View SolutionThe electric potential between a proton and an electron is given by `V= V_(0) ln ((r )/r_(0))` , where `r_(0)` is a constant . Assuming Bohr's model to be applicable, write variation of `r_(n)` with `n`, `n` being the principal quantum number ?
View SolutionAssertion: It is not essential that all the lines available in the emission spectrum will also be available in the absorption spectrum.
Reason: The spectrum of hydrogen atom is only absorption spectrum.
View SolutionAssertion: In a hydrogen atom energy of emitted photon corresponding to transition from `n = 2` to `n = 1` is much greater as compared to transition from `n=oo` to `n = 2`.
Reason: Wavelength of photon is directly proportional to the energy of emitted photon.
View Solution
Section D - Chapter End Test questions and complete solutions for chapter ATOMIC PHYSICS of A2Z PHYSICS (HINGLISH) of Class 12